
中国海洋湖沼学会主办。
文章信息
- 伊锋, 房克照, 孙家文, 王平, 吴浩, 尤再进, 李彬. 2022.
- YI Feng, FANG Ke-Zhao, SUN Jia-Wen, WANG Ping, WU Hao, YOU Zai-Jin, LI Bin. 2022.
- 渗透潜堤对沙滩剖面演化影响的物理模型试验研究
- LABORATORY STUDY ON BEACH PROFILE EVOLUTION UNDER THE PROTECTION OF SUBMERGED POROUS BREAKWATER
- 海洋与湖沼, 53(4): 951-959
- Oceanologia et Limnologia Sinica, 53(4): 951-959.
- http://dx.doi.org/10.11693/hyhz20211200307
文章历史
-
收稿日期:2021-12-01
收修改稿日期:2022-02-21
2. 国家海洋环境监测中心 辽宁大连 116023;
3. 大连海事大学港口与航运安全协同创新中心 辽宁大连 116026
2. National Marine Environmental Monitoring Center, Dalian 116023, China;
3. Centre for Ports and Maritime Safety, Dalian Maritime University, Dalian 116026, China
潜堤作为海滩修复和侵蚀防护工程中运用较为广泛的构筑物, 有消减入射波能量、减少滩面侵蚀和维护沙滩稳定的效果。同时潜堤淹没于水下, 相比于丁坝、出水堤等有更好的海岸景观效果; 其具有较大的孔隙率, 有利于附着生物生长和海水交换, 维护生物多样性和保护近海生态环境(谢琳等, 2014), 因此研究渗透潜堤对沙滩剖面演化的影响具有重要意义。
潜堤透射系数是衡量潜堤消浪能力、防止沙滩侵蚀的重要指标。Seabrook等(1998)通过物理模型实验研究了不同水深、波浪要素和潜堤形式的组合对抛石堤透射系数影响, 并根据结果拟合出透射系数经验公式; 孙天霆等(2018)采用断面物理模型实验方法, 研究了波浪与渗透潜堤的相互作用关系, 讨论了潜堤无量纲参数(淹没水深与波高之比、波高与周期之比、堤心石粒径与波高之比等)与堤后透射系数的关系, 并在物理模型实验基础上提出规则波作用下透射系数的经验计算公式; 同样, 冯卫兵等(2012)通过物理模型实验研究分析了各种因素(相对淹没水深、波陡、相对堤顶宽度)组合下堤后透射系数的变化规律。也有一些学者关注潜堤附近波浪传播变形及流场细部结构特征(蒋昌波等, 2008, 2009; 陈杰等, 2009, 2011)。
Özölçer(2008)根据沙滩剖面物理模型实验数据评估了不同波浪要素和海滩形态参数对沙滩侵蚀量的相对影响, 指出波高是影响沙滩侵蚀程度的主要因素, 并建议将沙滩侵蚀量以入射波高进行无因次处理(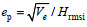
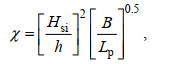 (1)
(1)式中, Hsi、Lp、h和B分别为入射有效波高、波长、潜堤处水深、堤顶宽度。研究表明, 在潜堤附近底床呈淤积趋势, 对于较小χ的值更为明显; 随着χ的增加, 淤积量逐渐减小。Lorenzoni等(2016)通过沙滩剖面动床物理模型实验给出了考虑潜堤高度的χ表达式:
 (2)
(2)式中, hstr为潜堤高度。Lorenzoni等(2016)指出透射系数与χ存在很强的关联性, 但未建立沙滩剖面侵蚀量与χ的量化关系。Mojabi(2018)应用Delft3d开展了大量数值模拟研究, 给出了综合考虑潜堤相对淹没深度(Rc/Hrmsi)和孔隙率(n)的χ表达式:
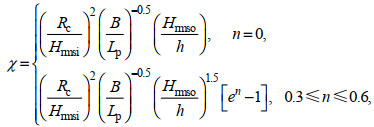 (3)
(3)式中, Hrmso是深水均方根波高。当潜堤孔隙率n=0时, 沙滩侵蚀量最大, 随着孔隙率从0.6到0.3逐渐减小, 沙滩侵蚀量逐渐变小。基于此, Mojabi(2018)建立了渗透潜堤存在时沙滩侵蚀量的估算公式:
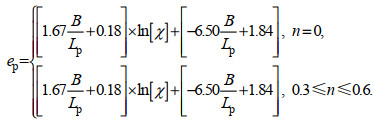 (4)
(4)需要注意, 该公式主要基于数值模型实验研究得到, 其适用范围和精度尚需进一步探究。
综上可知, 当前关于潜堤的研究多集中于波浪透射系数、波浪传播变形以及局地流场等水动力方面, 对可渗透潜堤影响下沙滩剖面演化的研究相对较少。本文在波浪水槽中开展沙滩剖面动床物理模型实验, 研究规则波和JONSWAP谱随机波浪作用下渗透潜堤对沙滩剖面演化的影响, 重点分析波浪传播演化的相关水动力特征和沙滩剖面侵淤变化, 给出综合考虑渗透形态特征和波浪条件的无量纲参数χ的表达式, 并建立沙滩侵蚀量的估算公式。
1 实验方案 1.1 实验布置与设计实验在大连理工大学海岸和近海工程国家重点实验室海洋环境水槽进行, 水槽长69 m, 宽2 m, 高1.8 m, 水槽一端配有推板式造波机。沿轴线将水槽分隔为宽度为1.2 m和0.8 m两部分, 实验在宽0.8 m的水槽中开展, 水深0.55 m, 平滩高0.2 m。图 1为实验布置图, 静水面与水槽末端交点为原点, 垂直向上为z轴正向, 波浪传播方向为x轴负向。沙滩模型长20 m, 由中值粒径0.24 mm的天然沙组成, 近岸沙滩坡度1:8, 其前设置为5.2 m宽的平坦台地以便于渗透潜堤模型的安放, 离岸侧沙滩坡度1:50。
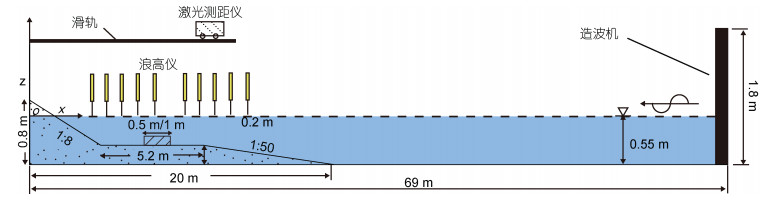 |
| 图 1 实验布置示意图 Fig. 1 Sketch of the experimental setup |
渗透潜堤尺寸和安放位置在图 2中给出。渗透潜堤由大孔隙块体组成, 孔隙率为70.32%。堤顶宽度为1 m和0.5 m (对应表 1波况1, 取实验最大波长1/4和1/8); 根据先前学者水槽实验(蒋昌波等, 2014)并结合本次实验条件, 堤顶水深取0.15 m, 则潜堤高0.2 m; 潜堤长0.8 m, 与水槽宽度一致。依据工况设置不同, 潜堤安放位置分别位于平坦沙滩台地的离岸侧(a)、中部(b)和近岸侧(c)。
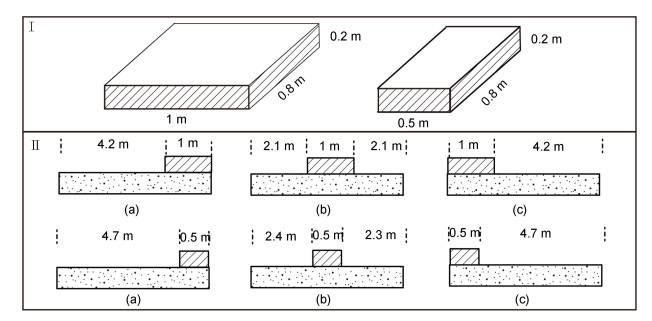 |
| 图 2 渗透潜堤形状与安放位置示意图 Fig. 2 Sketch of the layout of submerged porous breakwater 注: I. 渗透潜堤形状; II. 安放位置 |
| 波况 | d/m | Hs/m | T/s | L/m | Cs | 备注 |
| 1 | 0.55 | 0.18 | 1.9 | 4.0 | 20.93 | 规则波 |
| 2 | 0.55 | 0.14 | 1.6 | 3.2 | 17.50 | 规则波 |
| 3 | 0.55 | 0.16 | 1.7 | 3.4 | 19.49 | JONSWAP |
Sunamura等(1974)提出岸滩剖面类型判断准则如下:
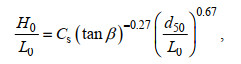 (5)
(5)式中, H0为深水波高, L0为深水波长, tanβ为初始近岸沙滩坡度, Cs为沙滩侵蚀类型无量纲指标。对于物理模型实验, 当Cs≥8时为侵蚀型沙滩剖面, 4≤ Cs≤8为过渡型沙滩剖面, Cs≤4为淤积型沙滩剖面。依据公式(5)确定侵蚀型沙滩剖面对应的波要素并列入表 1, 其中d为水深, Hs为有效波高, T为有效周期(J谱指谱峰周期)。
依据波要素、渗透潜堤宽度和安放位置不同, 共计21个实验工况, 列于表 2。表中, B为堤顶宽度, P为潜堤安放位置。为便于对比分析, 每组波况设置一个无潜堤工况作为对比实验(工况1、工况8和工况15)。
| 工况 | Hs/m | T/s | B/m | P | 备注 | 工况 | Hs/m | T/s | B/m | P | 备注 | |
| 1* | 0.18 | 1.9 | — | — | 规则波 | 12 | 0.14 | 1.6 | 1 | a | 规则波 | |
| 2 | 0.18 | 1.9 | 0.5 | a | 规则波 | 13 | 0.14 | 1.6 | 1 | b | 规则波 | |
| 3 | 0.18 | 1.9 | 0.5 | b | 规则波 | 14 | 0.14 | 1.6 | 1 | c | 规则波 | |
| 4 | 0.18 | 1.9 | 0.5 | c | 规则波 | 15* | 0.16 | 1.7 | — | — | JONSWAP | |
| 5 | 0.18 | 1.9 | 1 | a | 规则波 | 16 | 0.16 | 1.7 | 0.5 | a | JONSWAP | |
| 6 | 0.18 | 1.9 | 1 | b | 规则波 | 17 | 0.16 | 1.7 | 0.5 | b | JONSWAP | |
| 7 | 0.18 | 1.9 | 1 | c | 规则波 | 18 | 0.16 | 1.7 | 0.5 | c | JONSWAP | |
| 8* | 0.14 | 1.6 | — | — | 规则波 | 19 | 0.16 | 1.7 | 1 | a | JONSWAP | |
| 9 | 0.14 | 1.6 | 0.5 | a | 规则波 | 20 | 0.16 | 1.7 | 1 | b | JONSWAP | |
| 10 | 0.14 | 1.6 | 0.5 | b | 规则波 | 21 | 0.16 | 1.7 | 1 | c | JONSWAP | |
| 11 | 0.14 | 1.6 | 0.5 | c | 规则波 | |||||||
| 注: 右上角*号表示该工况无渗透潜堤 | ||||||||||||
实验开始前, 在水槽中率定波浪, 使得波高和周期满足给定的模型波浪要素值, 然后沿设计沙滩剖面填入天然沙, 淹没浸泡12 h后, 排水调整沙滩模型直至满足精度要求。预实验表明波浪作用大约150 min后沙滩剖面几乎不发生变化, 达到平衡。造波时间持续150 min, 期间使用精度为0.1 mm的LG-1电阻式浪高仪同步采集沿程波面变化。为避免波浪二次反射, 采用间歇方式造波, 每组波列的持续时间约为10 min, 待水面静止后开始下一轮造波。每组工况结束后将水槽中的水缓慢排出以避免水流引起沙滩剖面冲蚀, 滩面完全露出后, 采用激光测距仪采集沙滩高程。激光测距仪沿沙滩模型上方的轨道滑行, 其高程测量精度为1 mm, 沿水槽方向每间隔2 cm获取一次沙滩高程。
2 结果与分析 2.1 水动力演化分析 2.1.1 波高空间分布与透射系数使用上跨零法统计分析波高, 进而得到透射系数, 其定义如下:
 (6)
(6)式中, Ht是潜堤后方的透射波高, 采用潜堤到岸线波高的平均值(以忽略堤后沙滩处的波浪反射带来的影响), Hi是潜堤前方的入射波高, 这里取入射波高(0.18 m、0.16 m和0.14 m), 以避免潜堤附近的反射波带来的干扰。
图 3为代表性工况(15、16、17、18)沙滩剖面达到平衡后波高的沿程分布(由于堤顶上方水深较小, 不方便浪高仪布置, 浪高数据缺失), 表 3为透射系数汇总。可见, 无潜堤时, 波高沿程分布变化较小; 有潜堤时, 堤前离岸区波高基本一致, 波浪向岸传播过程中遇到潜堤后, 水深变浅, 波浪在堤顶发生破碎, 导致堤后波高降低, 因此潜堤可以有效消耗波能, 减小作用到堤后滩面的能量, 保护堤后沙滩。需要提到的是潜堤反射和渗透潜堤大孔隙介质产生的流动阻力也是堤后波高降低的原因。
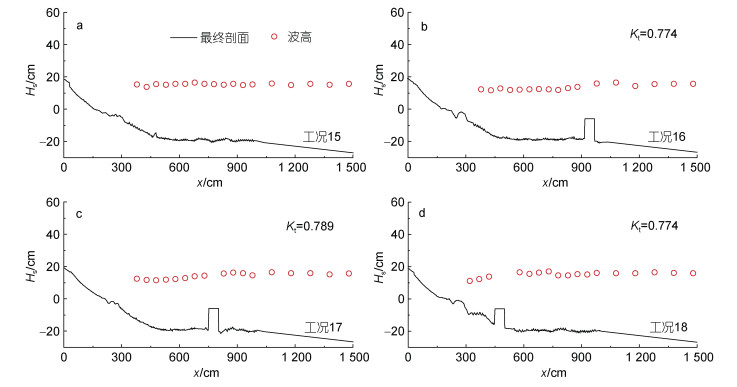 |
| 图 3 波高空间分布与透射系数 Fig. 3 The spatial variation of wave height and transmission coefficient |
| 工况 | Kt | 工况 | Kt | 工况 | Kt | ||
| 1 | — | 8 | — | 15 | — | ||
| 2 | 0.928 | 9 | 0.977 | 16 | 0.774 | ||
| 3 | 0.843 | 10 | 0.845 | 17 | 0.789 | ||
| 4 | 0.984 | 11 | 0.899 | 18 | 0.774 | ||
| 5 | 0.879 | 12 | 0.894 | 19 | 0.741 | ||
| 6 | 0.812 | 13 | 0.833 | 20 | 0.713 | ||
| 7 | 0.922 | 14 | 0.838 | 21 | 0.760 |
由表 2与表 3可知, 在同一波浪条件下, 当潜堤安放位置相同时, 堤顶宽度越大, 透射系数越小, 潜堤消浪效果越好; 同一波浪条件下, 当坝顶宽度相同, 潜堤位置不同时, 透射系数的变化趋势不明显, 说明对于所考虑的实验工况, 潜堤位置与透射系数的关联性不明显。
2.1.2 频谱使用FFT快速傅里叶变化统计分析频谱变化。图 4为工况19沙滩剖面达到平衡时渗透潜堤前后的频谱对比, 对应的无潜堤工况15也一并给出。可见, 对于两种工况, 离岸深水处入射波的频谱结构基本保持一致, 能量主要分布在基频(f=0.58 Hz)附近, 谱峰值约为160~162 m2⋅s。无潜堤时, 频谱由堤前向堤后沿程变化较小, 这表明波浪能量几乎全部作用于堤后滩面, 可能会对沙滩剖面造成严重侵蚀; 有潜堤时, 波浪越过潜堤向岸传播的过程, 频谱形态发生了较大变化, 基频能量幅值急剧下降至52 m2⋅s。由于潜堤存在引起的反射、波浪提前破碎和大孔隙介质产生的流动阻力, 显著消耗了本该传至岸线附近的入射波能量, 有效防止了堤后岸滩侵蚀。
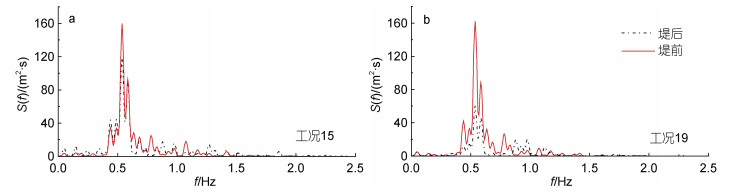 |
| 图 4 频谱空间变化 Fig. 4 The spatial variation of wave spectrum |
波浪的偏度(Sk)和斜度(As)作为波浪非线性和向岸泥沙输运的关键参数(Peng et al, 2009), 其定义如下:
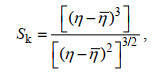 (7)
(7)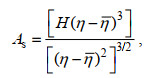 (8)
(8)式中, η为波面升高, H为希尔伯特变换[]表示时间平均运算。
波浪偏度Sk (波面关于水平轴的不对称程度, 即波峰与波谷的不对称程度)和波浪斜度As (波浪剖面的不对称性, 即波浪的前坡与后坡陡峭程度的不对称性)对浅滩区和冲泄区的陆上泥沙输运有至关重要的作用。图 5为典型工况(15、17、20、21)岸滩剖面平衡后波浪偏度和斜度空间分布。偏度与斜度在堤前近海区域较小, 非线性较弱。无潜堤时, 偏度由深水(Sk=0.31)到浅水(Sk=0.65)呈逐步增加趋势, 偏度正值反映波峰的高和尖、波谷平而浅的趋势。斜度由深水(As=0.03)到浅水(As=–0.53)呈逐步减小趋势, 斜度正值表明破碎波剖面的前坡陡于后坡, 即陡峭的前坡和平缓的后坡, 波剖面向前倾斜。
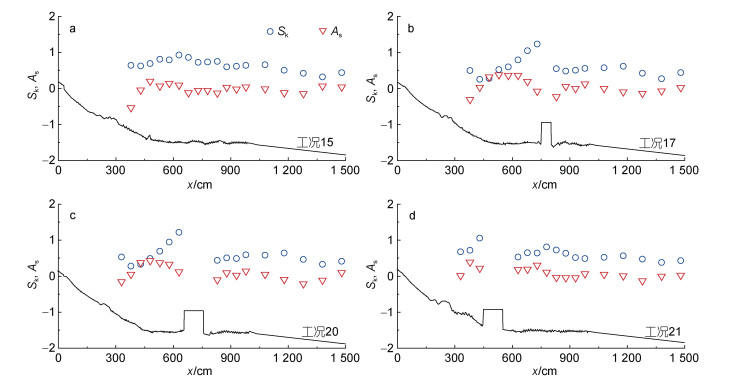 |
| 图 5 波浪偏度与斜度空间分布 Fig. 5 The spatial variation of Sk and As |
波浪非线性沿程变化受潜堤影响较大。由图 5可知, 波浪由堤前传播至堤后, 偏度Sk急剧增大, 而斜度As值随波浪由堤前-堤后-岸线先增大后减小, 这表明波浪在遇到结构物后, 局部波浪非线性效应增强。波浪在潜堤上传播过程较为复杂, 包含波浪重组、波波相互作用、高阶谐波产生、波浪破碎等, 当波浪传播到潜堤上时, 受浅水效应影响, 非线性效应增强, 波浪变形使得波峰变尖, 波谷变平。潜堤迎浪侧的Sk明显小于背浪侧, As从深水到堤后呈增加趋势, 继续向岸线传播的过程, As呈减小趋势, 这些与波浪在堤顶破碎和堤后波浪重组有关。
2.2 沙滩剖面演化分析沙滩剖面演化由泥沙质量守恒方程控制(Grasso et al, 2011):
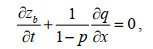 (9)
(9)式中, zb是底床高程, t为时间, p为泥沙孔隙率, 这里取0.4, q为输沙率。则根据沙滩高程变化可得到平均输沙率q(Baldock et al, 2011):
 (10)
(10)式中, q > 0表示泥沙向岸输运, q < 0对应于泥沙离岸输运。
2.2.1 平均输沙率沙滩剖面演变是泥沙离岸输运和向岸输运之间平衡的结果, 泥沙离岸输运主要是由波浪破碎相关的近海海底回流引起的(Van Der Zanden et al, 2017), 而向岸运动与波浪非线性相关。图 6为典型工况(1、2、9、10、16、17)岸滩演变与平均输沙率空间分布。由图 6可知, 近岸泥沙以离岸输运为主。无潜堤时, 平均离岸输沙率最大可达13.7× 10–6 m2/s; 有潜堤时, 近岸离岸输沙率显著减小, 表明潜堤可有效保护降低堤后岸滩的侵蚀程度。
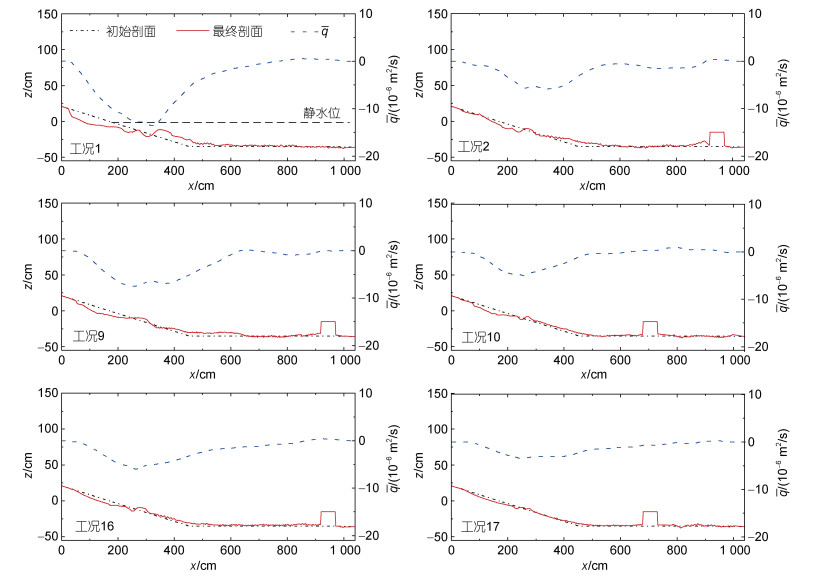 |
| 图 6 岸滩演变与平均输沙率空间分布 Fig. 6 The spatial variation of beach profile evolution and mean sand transport rate |
经过150 min波浪作用, 岸线处侵蚀较为严重, 同时近岸斜坡滩面形成水下沙坝堆积体, 沙坝形态因潜堤安放位置、坝顶宽度和波浪要素的不同而异。其中入射波高越大, 形成的沙坝体积越大。堤后到岸线区域, 泥沙以离岸输运为主, 波浪在堤顶破碎, 在破波带内水体产生强烈紊动, 将滩面泥沙掀起, 离岸输运使得岸线处侵蚀较为严重, 一部分泥沙在破波点处沉降淤积, 形成水下沙坝, 另一部分继续离岸输运; 潜堤向岸侧呈淤积状态, 因为波浪破碎使大量泥沙悬浮, 在海底回流作用下, 泥沙离岸输运, 运动至堤后平滩淤积。
3 讨论 3.1 沙滩剖面侵蚀指标统计分析ep表示单位入射波高的沙滩侵蚀, pi表示潜堤对滩面防护效果的一种度量, 又称“沙滩保护指数” (Özölçer(2008)), 其定义如下:
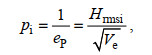 (11)
(11)式中, ep值越小说明沙滩侵蚀量越小, pi值越大说明沙滩保护效果越好。
图 7为沙滩剖面各侵蚀指标示意图, 包括岸线后退距离、静水位与原始剖面相交处侵蚀深度和沙滩侵蚀量(仅统计近岸滩面侵蚀量, 阴影部分)。
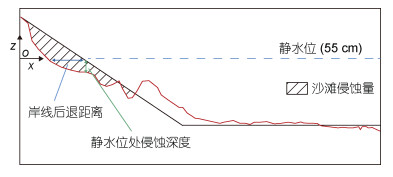 |
| 图 7 沙滩各侵蚀指标示意图 Fig. 7 Sketch of beach evolution |
表 4为沙滩剖面侵蚀指标统计汇总。工况3的ep为1.09, 为最小值; pi为0.91, 为最大值, 因此对于实验考虑工况, 工况3潜堤位置、坝顶宽度与波浪要素对沙滩的防护效果最好。
| 工况 | 波高/m | 静水位处侵蚀深度/cm | 岸线蚀退距离/cm | 单宽侵蚀量/(m3/m) | ep | pi | |
| 1* | 0.18 | 7.6 | 96 | 0.212 | 2.55 | 0.39 | |
| 2 | 4.4 | 26 | 0.073 | 1.50 | 0.66 | ||
| 3 | 1.5 | 10 | 0.039 | 1.09 | 0.91 | ||
| 4 | 6.1 | 54 | 0.122 | 1.94 | 0.51 | ||
| 5 | 1.6 | 12 | 0.046 | 1.19 | 0.83 | ||
| 6 | 4.2 | 50 | 0.081 | 1.58 | 0.63 | ||
| 7 | 8.1 | 48 | 0.108 | 1.82 | 0.54 | ||
| 8* | 0.14 |
5.9 | 50 | 0.082 | 2.04 | 0.48 | |
| 9 | 6.1 | 62 | 0.113 | 2.40 | 0.41 | ||
| 10 | 5.8 | 46 | 0.075 | 1.95 | 0.51 | ||
| 11 | 8.2 | 66 | 0.098 | 2.23 | 0.44 | ||
| 12 | 4.9 | 42 | 0.077 | 1.98 | 0.50 | ||
| 13 | 3.9 | 40 | 0.061 | 1.76 | 0.56 | ||
| 14 | 6.0 | 50 | 0.088 | 2.11 | 0.47 | ||
| 15* | 0.16 | 6.6 | 54 | 0.124 | 2.20 | 0.45 | |
| 16 | 5.1 | 40 | 0.073 | 1.68 | 0.59 | ||
| 17 | 3.2 | 28 | 0.050 | 1.39 | 0.71 | ||
| 18 | 4.8 | 50 | 0.099 | 1.96 | 0.50 | ||
| 19 | 3.6 | 42 | 0.062 | 1.55 | 0.64 | ||
| 20 | 3.5 | 30 | 0.066 | 1.60 | 0.62 | ||
| 21 | 6.3 | 40 | 0.080 | 1.76 | 0.56 | ||
| 注: 右上角*号表示该工况无渗透潜堤 | |||||||
由表 4可知, 无潜堤时, 静水位处侵蚀深度、岸线蚀退距离、侵蚀量与ep等指标较大; 放置潜堤后, 这些指标均大大减少, 潜堤对防护滩面侵蚀具有积极作用。总体看来, 堤顶越宽, 各项侵蚀指标值越小, 对滩面保护作用越强。当潜堤安放位置不同时, 很难在表 4中找到侵蚀指标明显的变化趋势, 说明滩面防护效果与潜堤位置联系较小。
图 8所示为有潜堤时不同工况对应的ep与pi, 共有6组对比, 每组对比潜堤顶宽度与安放位置一致, 而波高从左到右依次降低。随着波高的逐渐降低, ep依次升高, pi依次降低, 说明潜堤在较大波高下, 对沙滩有更好的保护效果。
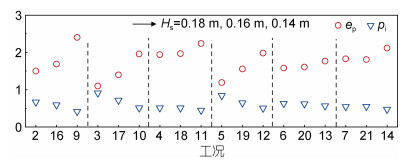 |
| 图 8 不同工况对应的ep与pi Fig. 8 The variations of ep and pi in different test cases |
沙滩侵蚀参数ep与潜堤特征参数χ关系可表达为:
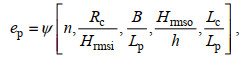 (12)
(12)式中, ψ是待求函数, Lc/Lp表示相对离岸距离(Lc为潜堤安放位置)。为了寻求函数ψ, 公式(12)中自变量可进行自由组合。
考虑到实验中渗透潜堤安放于平滩沙滩台地, 文献中提出的Hrmso/h因子组合型式可能不适用。综合前人研究成果(Lorenzoni et al, 2016; Postacchini et al, 2016; Mojabi, 2018), 结合本实验工况, 提出适用于平滩潜堤特征参数χ的表达式:
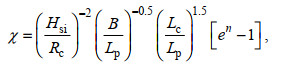 (13)
(13)式中, 潜堤孔隙率n=0.703 2, Lc为潜堤至平滩中轴线的距离(图 9所示)。可见, 式(13)考虑了潜堤淹没深度、堤顶宽度、安放位置以及孔隙率。将χ与ep进行非线性曲线拟合, 结果绘于图 10可见, 实验数据与曲线吻合程度较高(R2=0.855 3), 随着χ的增大, 近岸沙滩侵蚀量逐渐增加, 增加速率逐渐变缓。
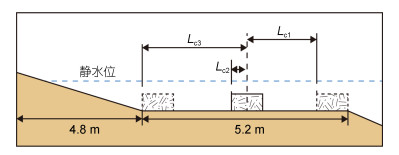 |
| 图 9 潜堤位置Lc示意图 Fig. 9 The positioning of submerged porous breakwater |
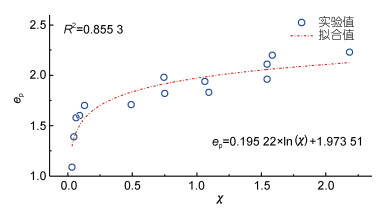 |
| 图 10 χ与ep曲线拟合方程 Fig. 10 The fitting equation of χ and ep |
本文开展了沙滩剖面动床物理模型实验, 研究了规则波和不规则波作用下渗透潜堤对沙滩剖面演化的影响, 得到以下主要结论:
(1) 潜堤具有明显消浪作用和沙滩防侵蚀效果; 当波浪传播到潜堤上时, 受浅水效应影响, 波浪破碎, 堤后波高降低, 同时基频能量下降, 波浪非线性效应增强。
(2) 近岸泥沙以离岸输运为主, 沙滩岸线处侵蚀较为严重, 同时斜坡滩面上形成沙坝堆积体, 潜堤向岸侧呈淤积状态, 这些与波浪破碎和海底回流有关。
(3) 滩面防护效果与潜堤安放位置联系较小; 堤顶宽度越大, 消浪效果越好, 滩面保护作用越强; 潜堤对于较大的波高有更好的沙滩防侵蚀效果。
(4) 提出了适用于平滩潜堤无量纲特征参数χ的表达式, 并建立了沙滩侵蚀量ep的估算公式。结果表明, 随着χ的增大, 近岸沙滩侵蚀量逐渐增加, 增加速率逐渐变缓。
冯卫兵, 王明明, 崔川川, 2012. 潜堤透浪系数的试验研究. 水运工程, (9): 1-6 DOI:10.3969/j.issn.1002-4972.2012.09.001 |
孙天霆, 刘清君, 王登婷, 2018. 可渗潜堤波浪透射系数试验研究. 水运工程, (4): 20-25, 42 DOI:10.3969/j.issn.1002-4972.2018.04.004 |
陈杰, 蒋昌波, 邓斌, 等, 2009. 波浪通过斜坡上潜堤的波能演化实验研究. 水动力学研究与进展A辑, 24(4): 417-424 |
陈杰, 蒋昌波, 刘虎英, 等, 2011. 潜堤对破碎区至冲泻区水动力特性影响数值分析. 水科学进展, 22(3): 382-390 |
蒋昌波, 肖桂振, 陈杰, 等, 2014. 潜堤影响下的沙质岸滩剖面变化实验研究. 海岸工程, 33(2): 37-44 DOI:10.3969/j.issn.1002-3682.2014.02.005 |
蒋昌波, 陈杰, 肖政, 等, 2008. 斜坡床面潜堤作用下的波浪传播变形. 长沙理工大学学报(自然科学版), 5(3): 47-51, 57 DOI:10.3969/j.issn.1672-9331.2008.03.008 |
蒋昌波, 曹永港, 陈杰, 2009. 斜坡上梯形潜堤附近流动结构的数值研究. 水动力学研究与进展A辑, 24(3): 286-295 |
谢琳, 陈斌, 莫文渊, 2014. 潜堤在海滩整治与改造中的运用. 中国水运, 14(1): 179-181 |
BALDOCK T E, ALSINA J A, CACERES I, et al, 2011. Large-scale experiments on beach profile evolution and surf and swash zone sediment transport induced by long waves, wave groups and random waves. Coastal Engineering, 58(2): 214-227 |
GRASSO F, MICHALLET H, BARTHÉLEMY E, 2011. Experimental simulation of shoreface nourishments under storm events: a morphological, hydrodynamic, and sediment grain size analysis. Coastal Engineering, 58(2): 184-193 DOI:10.1016/j.coastaleng.2010.09.007 |
LORENZONI C, POSTACCHINI M, BROCCHINI M, et al, 2016. Experimental study of the short-term efficiency of different breakwater configurations on beach protection. Journal of Ocean Engineering and Marine Energy, 2(2): 195-210 |
MOJABI S M, 2018. Effect of porosity and submergence of detached homogeneous rubble mound breakwaters on wave transmission and short term coastal erosion- a numerical study [D]. Braunschweig: Technische Universitat Braunschweig: 159.
|
ÖZÖLÇER İ H, 2008. An experimental study on geometric characteristics of beach erosion profiles. Ocean Engineering, 35(1): 17-27 |
PENG Z, ZOU Q P, REEVE D, et al, 2009. Parameterisation and transformation of wave asymmetries over a low-crested breakwater. Coastal Engineering, 56(11/12): 1123-1132 |
POSTACCHINI M, RUSSO A, CARNIEL S, et al, 2016. Assessing the hydro-morphodynamic response of a beach protected by detached, impermeable, submerged breakwaters: a numerical approach. Journal of Coastal Research, 32(3): 590-602 |
SEABROOK S R, HALL K R, 1998. Wave transmission at submerged rubblemound breakwaters [C] // Proceedings of the 26th International Conference on Coastal Engineering. Copenhagen, Denmark: ASCE.
|
SUNAMURA T, HORIKAWA K, 1974. Two dimensional beach transformation due to waves [C] // Proceedings of the 14th International Conference on Coastal Engineering. Copenhagen, Denmark: ASCE.
|
VAN DER ZANDEN J, VAN DER A D A, HURTHER D, et al, 2017. Bedload and suspended load contributions to breaker bar morphodynamics. Coastal Engineering, 129: 74-92 |
 2022, Vol. 53
2022, Vol. 53


