
中国海洋湖沼学会主办。
文章信息
- 王心玉, 赵晶, 王海峰, 王绿卿, 刘勇. 2022.
- WANG Xin-Yu, ZHAO Jing, WANG Hai-Feng, WANG Lyu-Qing, LIU Yong. 2022.
- 双消浪室局部开孔沉箱防波堤反射特性的理论与试验研究
- ANALYTICAL AND EXPERIMENTAL STUDIES ON THE REFLECTION CHARACTERISTICS OF PARTIALLY PERFORATED CAISSON BREAKWATER WITH DOUBLE WAVE CHAMBERS
- 海洋与湖沼, 53(4): 960-971
- Oceanologia et Limnologia Sinica, 53(4): 960-971.
- http://dx.doi.org/10.11693/hyhz20211200321
文章历史
-
收稿日期:2021-12-10
收修改稿日期:2022-02-22
2. 中国人民解放军91053部队 北京 100071
2. Unit 91053 of the Chinese People's Liberation Army, Beijing 100071, China
开孔沉箱在20世纪60年代由Jarlan (1961)首次提出, 其基本结构型式是将传统沉箱的前墙开孔, 在前开孔墙和后实体墙之间形成消浪室。相比传统不开孔沉箱结构, 波浪经过前开孔墙导致波能耗散, 并使消浪室内流体发生剧烈紊动耗能, 开孔沉箱可以有效降低堤前波浪反射、抑制结构越浪, 降低结构波浪力和工程造价(Huang et al, 2011; Liu et al, 2018)。因此, 开孔沉箱已在国内外海岸工程建设中得到广泛应用, 主要用于修建防波堤和码头等港口水工建筑物。
对于全开孔沉箱结构(开孔墙沿整个水深方向开孔且消浪室内外水深相等), Chwang等(1984)基于线性势流理论对结构的反射特性进行了研究, 发现反射系数随相对消浪室宽度B/L (B为消浪室宽度, L为入射波波长)呈周期性变化, 当B/L=0.25时反射系数最小。Suh等(1995)采用伽辽金方法对斜向波作用下带明基床全开孔沉箱的反射特性进行研究, 发现: 与正向波入射情况不同, 开孔沉箱结构在Bcos(θ/L)= 0.25时(θ为波浪入射角度)反射系数达到最小。Zhu等(2001)理论和试验研究了波浪作用下全开孔沉箱结构的反射特性, 发现: 当开孔墙的开孔率为0.2时, 结构消浪性能最佳。Teng等(2004)理论研究了斜向波作用下带横隔板全开孔沉箱防波堤的漫反射特性。Liu等(2016)利用速度势分解技术和匹配特征函数展开法建立了斜向波对带开孔横隔板全开孔沉箱防波堤作用的理论解, 分析了开孔墙和开孔横隔板的开孔率变化对反射特性的影响。Wang等(2021)基于势流理论建立了规则波对带部分消浪装置开孔沉箱防波堤作用的三维迭代解析解, 采用非线性压力损失边界条件来考虑开孔墙处的能量耗散和波相位变化, 研究发现开孔墙位于沉箱中间且开孔墙长度与沉箱长度比值在0.3~0.5时, 带消浪装置的开孔沉箱防波堤消浪效果较好。Bennett等(1992)基于线性势流理论给出了不规则正向波作用下开孔板防波堤的反射谱和频率平均反射系数的计算方法, 并利用物理模型试验结果验证了方法的合理性。Suh等(2001)理论和试验研究了不规则波作用下全开孔沉箱结构的反射特性, 研究表明: 当B/Ls约等于0.2 (Ls为有效波长)时, 反射系数达到最小并随波陡的增加而减小。
为提高开孔沉箱的抗倾及抗滑稳定性, 可采用局部开孔沉箱结构(开孔墙仅在静水位附近开孔, 消浪室内部水深小于堤前水深)。Tanimoto等(1982)对波浪作用下局部开孔沉箱防波堤的反射特性进行了理论和试验研究, 给出了防波堤达到低反射的设计参数范围。李玉成等(2004)基于匹配特征函数法研究了相对消浪室宽度、开孔率和相对水深对局部开孔沉箱结构反射特性的影响规律。Suh等(2006)理论和试验研究了不规则波作用下带明基床的局部开孔沉箱防波堤的反射特性。Liu等(2007)引入周期性边界条件, 建立了斜向波对带横隔板局部开孔沉箱防波堤作用的三维解析模型, 分析了局部开孔沉箱防波堤的漫反射特性。
为进一步提高开孔沉箱的消浪性能, 许多学者对双消浪室(多消浪室)开孔沉箱结构的水动力特性开展了研究。Sawaragi等(1978)以及Kondo (1979)分析了正向波作用下双消浪室开孔沉箱的反射特性, 发现: 通过合理设计, 双消浪室开孔沉箱的消浪性能可明显优于单消浪室开孔沉箱。Huang (2006)基于时域势流理论研究了不规则波作用下多消浪室开孔结构的反射特性。Liu等(2012)利用匹配特征函数展开法研究了斜向波作用下双消浪室开孔防波堤的受力特性, 研究结果表明: 斜向波作用下双消浪室开孔防波堤具有更好的消浪效果; 在正向波作用下, 其承受的总水平波浪力也小于单消浪室开孔防波堤。Lee等(2014)通过物理模型试验对不规则波作用下单消浪室和双消浪室局部开孔沉箱防波堤的反射特性进行了对比研究, 试验发现: 对于单消浪室局部开孔沉箱, 前墙开孔率ε越小(0.2 < ε < 0.6), 反射系数越低; 对于双消浪室局部开孔沉箱, 当后开孔墙的开孔率小于前开孔墙的开孔率时, 其消浪性能优于单消浪室开孔沉箱。Zhao等(2020)研究了正向规则波作用下多消浪室局部开孔沉箱防波堤的反射特性, 发现当开孔墙的开孔率沿入射波传播方向依次减小时, 开孔沉箱防波堤的反射系数更低。Sammarco等(2021)基于黏性流模型建立了波浪对透空式交错排布的多消浪室局部开孔沉箱防波堤作用的数值模型, 通过数值和试验研究发现开孔墙的开孔率沿入射波传播方向依次减小且后开孔墙开孔率为2%时, 新型透空式开孔沉箱防波堤可以在保障水体交换的同时有效降低波浪的透射和反射。
与上述研究不同, 本文将研究斜向波作用下双消浪室局部开孔沉箱防波堤的反射特性, 建立规则波和不规则波对双消浪室局部开孔沉箱防波堤作用的三维理论解, 并开展相应的平面水池试验对理论解进行验证。理论解在开孔墙处采用二次压力损失边界条件(Molin, 2011; Molin et al, 2013; Liu et al, 2017)来考虑开孔墙对波能耗散和相位改变的影响。此外, 由于开孔沉箱内部横隔板的存在, 开孔沉箱防波堤在长度方向呈周期性变化, 本文将采用周期性边界条件(Evans et al, 1995; Linton et al, 2001; Porter et al, 2005)来考虑结构周期性变化对波浪运动的影响。最后, 通过算例分析与讨论, 研究相对消浪室宽度、波浪入射角度和前后开孔墙开孔率组合等对双消浪室局部开孔沉箱防波堤水动力特性的影响。本文建立理论解的过程和方法可为其他类似问题的三维理论建模和分析提供参考, 分析结果可为工程设计提供科学指导。
1 规则波对开孔沉箱防波堤作用的理论模型 1.1 控制方程和边界条件图 1给出波浪对双消浪室局部开孔沉箱防波堤作用的示意图。图 1左上角为一个结构单元, 其由两侧横隔板、前后排开孔墙和后实体墙组成。因开孔墙厚度和横隔板厚度远小于波长, 本文在理论模型建立过程中忽略开孔墙和横隔板厚度对波浪绕射的影响。一个结构单元的长度为l, 前消浪室宽度为B1, 后消浪室宽度为B2。采用三维笛卡尔坐标系来描述该问题, 坐标原点O位于某一侧板、后开孔墙以及静水面的交点处, x轴指向港池内侧, y轴沿防波堤轴线方向, z轴垂直向上。堤前水深为d1, 双消浪室内水深均为d2, 前、后墙开孔深度均为d3 (d3 < d2 < d1)。入射波高为H, 波长为L, 波浪入射角度为θ0 (0 ≤ θ0 < π/2)。
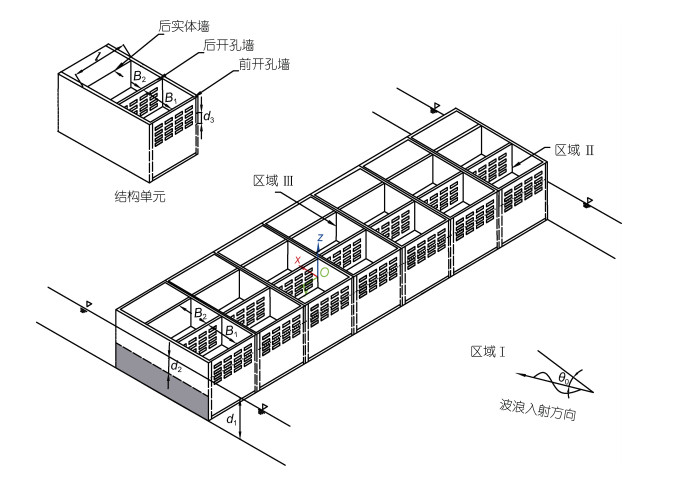 |
| 图 1 波浪对双消浪室局部开孔沉箱防波堤作用的示意图 Fig. 1 Sketch for wave acting on double wave-chamber partially perforated caisson breakwater 注: B1为前消浪室宽度, B2为后消浪室宽度; 坐标原点O位于某一侧板、后开孔墙以及静水面的交点处, x轴指向港池内侧, y轴沿防波堤轴线方向, z轴垂直向上; d1为堤前水深, d2为双消浪室内水深, d3为前、后墙开孔深度; θ0为波浪入射角度 |
考虑不可压缩无旋的理想流体, 流体运动可以用速度势Φ(x, y, z, t) 来表示。对于圆频率为ω的微幅波, 时间因子e-iωt可以从速度势中分离出来
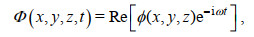 (1)
(1)其中, Re表示取复数的实部; 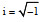
由图 1可知, 开孔沉箱防波堤沿y轴方向呈周期性变化, 采用周期性边界条件(Evans et al, 1995)来考虑结构周期性变化对波浪运动的影响, 周期性边界条件的表达式为
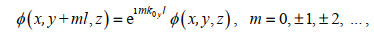 (2)
(2)其中, k0y为波数k0在y方向的分量, 满足k0y=k0sinθ0, 波数k0满足
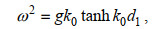 (3)
(3)其中, g为重力加速度。利用周期性边界条件, 可以先在一个结构单元所在的流体区域内(−∞ < x < +∞, 0≤y≤l)求解速度势, 然后利用公式(2)得到其他流域内的速度势。为求解方便, 把流体区域(−∞ < x < +∞, 0 ≤y≤l)分为三个子区域: 沉箱前半无限长流体域为区域I (x≤−B1, 0≤y≤l); 前消浪室内的流体域为区域II (−B1 < x≤0, 0≤y≤l); 后消浪室内的流体域为区域III (0 < x≤−B2, 0≤y≤l)。
空间速度势在各区域内满足拉普拉斯方程
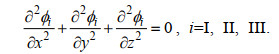 (4)
(4)速度势满足自由水面条件、海底条件及沉箱表面的物面条件
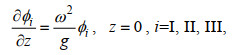 (5)
(5) (6)
(6)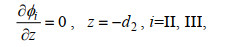 (7)
(7)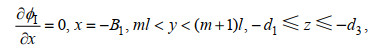 (8)
(8)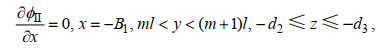 (9)
(9)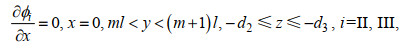 (10)
(10)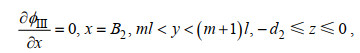 (11)
(11)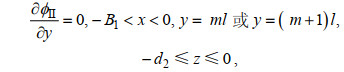 (12)
(12)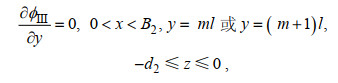 (13)
(13)其中, 空间速度势还满足相应的远场辐射条件。
当波浪经过开孔墙时, 流体会发生流动分离, 形成射流和涡流区, 导致波浪能量的耗散和波浪相位的改变。本文采用非线性压力损失边界条件(Liu et al, 2017)来考虑开孔墙的存在对波能耗散和波浪运动相位的影响, 其表达式为
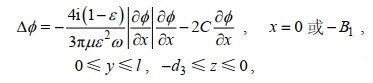 (14)
(14)其中, Δϕ为开孔墙两侧空间速度势的差, ε为开孔墙的开孔率, μ为射流系数, C为阻塞系数。公式(14)右侧第一项和第二项分别表示阻力(波能耗散)和惯性力(相位变化)的影响, 公式(14)右侧第一项还考虑了波高变化对波能耗散的影响。射流系数μ通常需要根据物理模型试验结果给出合理的取值。阻塞系数C可以采用经验公式(Suh et al, 2006)式(15)来计算:
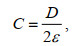 (15)
(15)值得注意的是, 本文仅在计算开孔墙阻塞系数C时考虑开孔墙厚度D。
1.2 速度势表达式应用分离变量法, 满足控制方程(4)和相关边界条件[式(5)~(7)、式(11)~(13)]的各区域速度势可写为
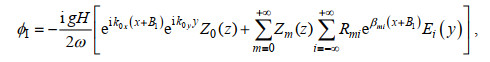 (16)
(16)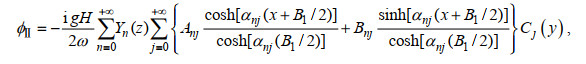 (17)
(17)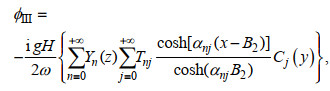 (18)
(18)其中, Rmi, Anj, Bnj和Tnj (m=0, 1, 2, …, n=0, 1, 2, …, i=±0, ±1, ±2, …, 和j=0, 1, 2, 3, …)为未知的特征展开系数。k0x=k0cosθ0为波数k0沿x方向的分量。Ei(y), Cj(y), Zm(z)和Yn(z)为特征函数, 其表达式分别为
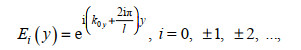 (19)
(19)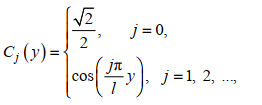 (20)
(20)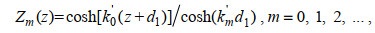 (21)
(21)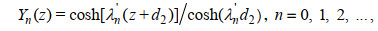 (22)
(22)其中, k0'=k0, km'=ikm(m≠0), km为色散方程ω2=-gkmtan(kmd1)(m=1, 2, …)的正实根; λ0'=λ0, λ0'=iλn(n ≠0), λ0和λn为正实数, 满足色散方程ω2=gλ0tan(λ0d2)=-gλntan(λnd2)(n=1, 2, …)。特征函数Ei(y), Cj(y), Zm(z)和Yn(z)满足正交关系
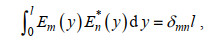 (23)
(23)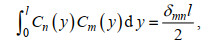 (24)
(24)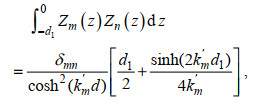 (25)
(25)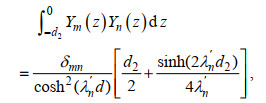 (26)
(26)其中, 星号表示函数的共轭复数, δmn是Kronecker Delta函数(δmn=1, m=n; δmn=0, m≠n)。以上正交关系将用来进行速度势展开系数的求解, 系数αnj和βmi由式(27)和式(28)计算
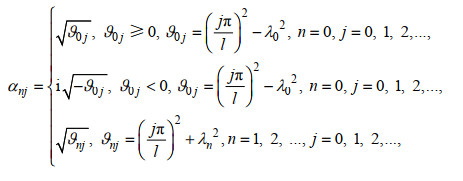 (27)
(27)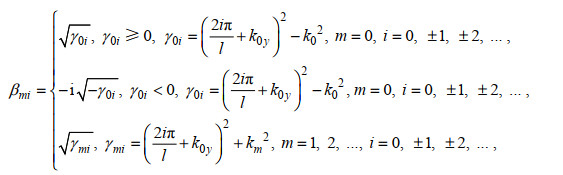 (28)
(28)其中, 系数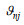
参考Fernyhough等(1995)关于波浪作用下周期性排列的矩形结构物水动力特性的研究, 定义如式(29):
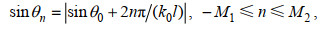 (29)
(29)其中: M1=Int[k0l(1+sinθ0)/2π], M2 =Int[k0l(1-sinθ0)/2π]; 符号Int表示对实数取整数部分, 夹角θn (−M1 ≤ n ≤ M2)为n阶反射波传播方向与x轴之间的夹角。通过式(29)可以看出, 各阶反射波的数目仅由入射波的波数k0、入射波角度θ0以及消浪室长度l决定。
利用匹配特征函数展开法求解各区域速度势中的未知展开系数, 由于开孔墙处采用了非线性压力损失边界条件, 需要对非线性方程组进行迭代求解(Liu et al, 2017), 具体求解过程见附录。
1.3 反射系数和自由面高度入射波和n阶反射波沿x轴方向的波能流分别为
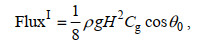 (30)
(30)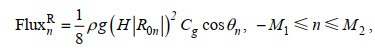 (31)
(31)其中, Cg为波浪群速度, ρ为流体密度。
开孔沉箱防波堤的n阶反射系数Rn定义为n阶反射波能量与入射波能量比值的平方根:
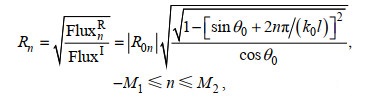 (32)
(32)其中, 零阶反射系数R0等于|R00|, 表示零阶反射波能量与入射波能量比值的平方根。开孔沉箱防波堤的总反射系数CR定义为各阶反射波能量之和与入射波能量比值的平方根
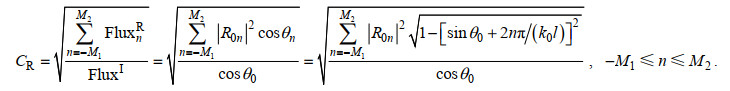 (33)
(33)结构物周围流体域I、II和III的波面ηI、ηII和ηIII表达式分别为
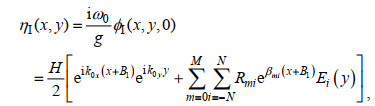 (34)
(34)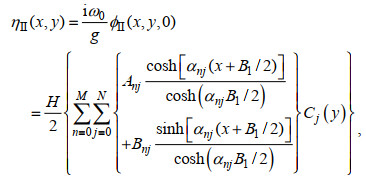 (35)
(35)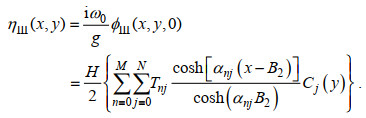 (36)
(36)对于本文新建立的理论解, 需要确定合理的速度势级数解的截断项数M和N, 以便得到收敛的计算结果。算例分析表明, 当M=25且N=5时, 可以得到收敛的计算结果(精确到小数点后三位), 因此, 在本文所有计算中均取M=25和N=5。本文还验证了迭代计算过程的收敛性, 发现迭代次数不超过20次, 就可以得到满足迭代精度要求(< 10–4)的计算结果。
2 不规则波对开孔沉箱作用的理论模型规则波对开孔沉箱防波堤作用的解析模型可通过传递函数法(Suh et al, 2001)扩展到不规则波作用的情况。对于线性叠加的不规则波, 各区域不规则波波面ξiir可表示为
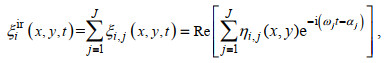 (37)
(37)其中, 下标i=I, II, III分别对应三个子流体域, ηi, j(x, y, t)表示i区域第j个组成波的波面表达式; J表示线性叠加的规则波个数; ωj和αj分别表示第j个组成波的角频率和初相位。
考虑不规则波的波浪谱Sηη(ω), 假定波浪能量主要分布在(ωL, ωH)频率区间内, 本文忽略低频(0, ωL)和高频(ωH, +∞)区间所占总能量的0.2% (俞聿修, 2000)。将区间(ωL, ωH)对应的波浪谱按角频率等分为J个组成波, 等分频率间隔Δωj=ωj-ωj-1=(ωH-ωL)/J, j=1, 2, …, J, ω0=ωL, ωJ=ωH。值得注意的是, 如果J取值较小, 则由计算机产生的随机数往往不够均布, 影响模拟结果的精度。参照Jacobsen等(2015)关于不规则波作用下透水海岸结构水动特性的数值研究, 本文取J=100。
要计算各组成波反射系数还需确定组成波的波高和代表频率。定义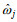
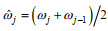
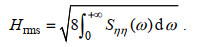 (38)
(38)确定各组成波的波高和代表频率后, 反射波频谱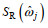
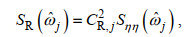 (39)
(39)则不规则波作用下双消浪室局部开孔沉箱防波堤反射系数CRir的表达式为
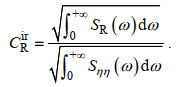 (40)
(40)物理模型试验在青岛某研究院波浪水池中进行。水池长42.5 m, 宽20 m, 深1.5 m。图 2给出物理模型试验波浪水池的现场照片, 图 3给出物理模型试验的平面布置示意图。如图 2所示, 波浪水池一端放置造波系统产生正向入射的规则波和不规则波, 靠近水池的另一端沉箱模型斜向摆放, 这样通过调整模型摆放的方向, 就可以考虑不同入射方向的斜向波对结构的作用。在水池末端和两侧放置消浪装置, 消减水槽末端和侧墙的波浪反射。试验比尺为1:30。
 |
| 图 2 物理模型及试验水池照片 Fig. 2 Photo of physical model and wave basin |
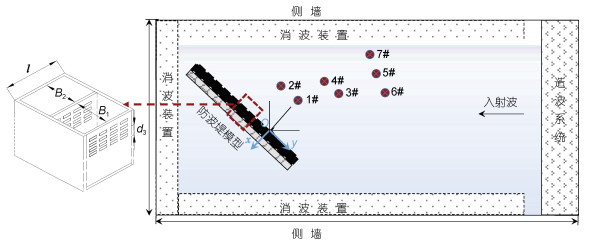 |
| 图 3 试验水池布置示意图 Fig. 3 Sketch of the experimental setup of the wave basin 注: B1为前消浪室宽度, B2为后消浪室宽度; d3为前、后墙开孔深度; l为单元沉箱长度 |
局部开孔沉箱防波堤模型是由15个混凝土浇筑而成的局部开孔沉箱结构单元组成, 每一个模型单元的尺寸为: 长0.63 m, 宽0.334 m, 高0.64 m。表 1列出了试验水深和试验模型参数。采用七根电容式波高仪测量堤前波面的时间序列。波高仪采样频率为50 Hz, 其采样精度为0.3% FS (full-scale, 全量程)。表 2列出了波高仪的编号及其坐标位置(坐标系见图 3)。采用孙昭晨等(1999)给出的入反射波分离方法, 分析斜向波作用下局部开孔沉箱防波堤的反射系数。
| 试验参数设置 | 取值 |
| 堤前水深d1/m | 0.500 |
| 消浪室内水深d2/m | 0.270 |
| 开孔深度d3/m | 0.090 |
| 前开孔墙厚度D1/m | 0.020 |
| 后开孔墙厚度D2/m | 0.010 |
| 前消浪室宽度B1/m | 0.167 |
| 后消浪室宽度B2/m | 0.167 |
| 沉箱长度l/m | 0.630 |
| 前开孔墙开孔率ε1 | 0.350 |
| 后开孔墙开孔率ε2 | 0.350 |
| 波高仪编号 | 坐标/m |
| 1# | (−1.200, 0.000) |
| 2# | (−1.220, −0.650) |
| 3# | (−2.230, 0.276) |
| 4# | (−2.412, 0.067) |
| 5# | (−3.346, 0.575) |
| 6# | (−3.226, 0.893) |
| 7# | (−3.508, 0.291) |
试验考虑了5种不同波浪周期的规则波和5种不同有效周期的不规则波。不规则波频谱采用JONSWAP谱(Goda, 1999)。表 3中列出规则波和不规则波的波要素, 5种规则波的波浪周期为T=1 s (k0d1=2.07)、1.1 s (k0d1=1.76)、1.19 s (k0d1=1.55)、1.28 s (k0d1=1.39)和1.37 s (k0d1=1.26), 5种不规则波有效周期为Ts=1.15 s、1.26 s、1.36 s、1.47 s和1.57 s。规则波波高H=0.05 m, 有效波高Hs=0.05 m, 入射波角度θ0=0°和15°。
| 规则波要素 | 不规则波要素 | |||
| 波高H/m | 周期T/s | 波长L/m | 有效波高Hs/m | 有效波周期Ts/s |
| 0.05 | 1.00 | 1.51 | 0.05 | 1.15 |
| 0.05 | 1.10 | 1.78 | 0.05 | 1.26 |
| 0.05 | 1.19 | 2.02 | 0.05 | 1.36 |
| 0.05 | 1.28 | 2.26 | 0.05 | 1.47 |
| 0.05 | 1.37 | 2.49 | 0.05 | 1.57 |
图 4给出规则波作用下防波堤反射系数计算结果和试验结果的对比, 图中算例的结构参数与试验模型参数相同。从图 4可看到, 当射流系数μ1=μ2=1.0时, 理论模型的计算结果与试验结果符合较好。因此, 在后续算例分析中, 取射流系数μ1=μ2=1.0。
 |
| 图 4 开孔沉箱防波堤反射系数理论结果与试验结果的对比 Fig. 4 Comparison in reflection coefficient of perforated caisson breakwater between analytical results and experimental results |
图 5给出试验频谱曲线和相应理论结果的对比。试验频谱曲线是由4#波高仪测量的波高时间序列经傅里叶变换得到。相应理论频谱曲线是由理论模型给出的波面时间序列经傅里叶变换计算得到。图中频率f和能谱密度S(f)分别由理论模型计算的谱峰频率fp和S(fp)进行无因次化。算例考虑了5种不同有效周期的不规则波。从图 5看出, 能谱密度随频率变化的理论结果和试验结果符合良好。值得注意的是, 在图 5中, 试验结果计算的能谱密度曲线在f < 0.1时存在能量分布, 而理论结果的能谱密度在该频率处无能量分布, 这是由于造波机刚启动时产生的长波造成的, 在本文分析中已通过傅里叶变换去掉此长波频率区间对应的波浪能量。
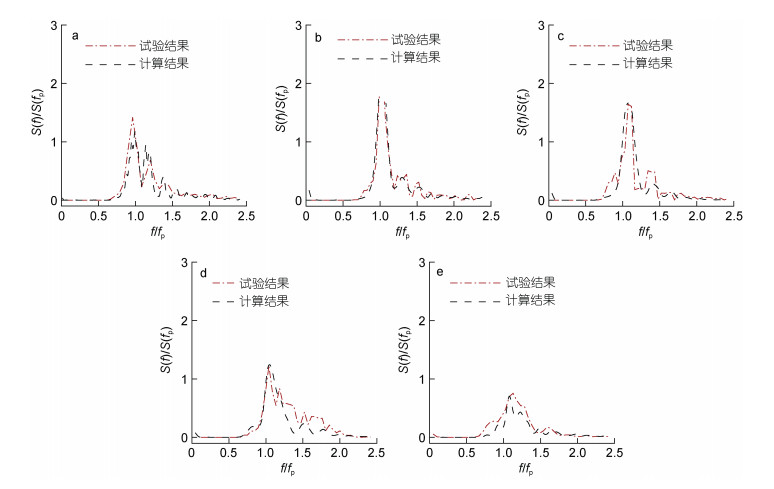 |
| 图 5 堤前4#波高仪处不规则波频谱的理论结果和试验结果对比 Fig. 5 Comparison between analytical results and experimental results of irregular wave spectrum at 4# wave gauge 注: a: Hs=0.05 m; b: Ts=1.15 s; c: Ts=1.26 s; d: Ts=1.36 s; e: Ts=1.47 s; f和fp分别为组成波频率和谱峰频率; S(f)和S(fp)分别为各组成波能谱密度和谱峰频率对应能谱密度 |
图 6给出规则波作用下双消浪室局部开孔沉箱防波堤CR随相对消浪室宽度(B1+B2)/L的变化曲线。算例的计算条件在图题中给出。可以看到, 随(B1+B2)/L增加, 局部开孔沉箱防波堤反射系数CR迅速减小到最小值。当k0d1=0.5时, 局部开孔沉箱防波堤反射系数在0.1 < (B1+B2)/L < 0.7之间反射系数较小。在k0d1=1.5~4.5时, 相对消浪室宽度在0.06 < (B1+B2)/L < 0.20时消浪效果较好。综合考虑实际工程设计, 局部开孔沉箱防波堤相对消浪室宽度(B1+B2)/L推荐0.08~0.20。
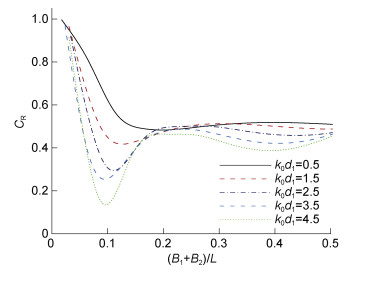 |
| 图 6 规则波作用下双消浪室局部开孔沉箱防波堤CR随相对消浪室宽度(B1+B2)/L的变化 Fig. 6 Variations in CR of perforated caisson breakwater versus (B1+B2)/L under the action of regular wave 注: 计算条件: ε1=0.35, ε2=0.25, B1/d1=B2/d1, l/d1=1.26, H/d1=0.1, d2/d1=0.54, d3/d1=0.18, θ0=π/12, 其中, ε1和ε2分别表示前后开孔墙开孔率; B1和B2分别为前、后消浪室宽度, l为单元沉箱长度, H为入射波高, d1为堤前水深, d2为双消浪室内水深, d3为前、后墙开孔深度; θ0为波浪入射角度 |
图 7给出双消浪室局部开孔沉箱防波堤CR随k0d1的变化曲线。图 7算例考虑了5种规则波波浪入射角度θ0=0, θ0=π/12, θ0=π/6, θ0=π/4, θ0=π/3和θ0=5π/12, 图中其他计算条件与图 6一致。当k0d1 < 0.5时, 随着θ0增大, CR略减小。当0.5 < k0d1 < 2时, 随着θ0从0增大到π/3, CR明显减小。当θ0=5π/12, 反射系数突然增大。当k0d1 > 2时, 由于多阶反射波的出现, 水动力参数发生突变, 其变化规律变得极为复杂。值得注意的是, 入射角度越大, 反射系数突变发生的波频k0d1越小。这主要是结构物的周期性排列导致在特定波频处出现了多阶反射波, 多阶反射波的出现使得水动力参数发生了突变(Teng et al, 2004; Wang et al, 2019)。
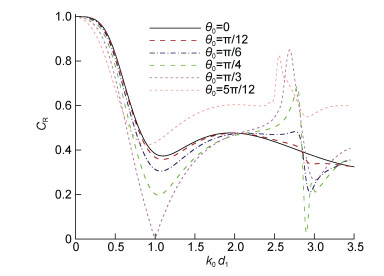 |
| 图 7 不同入射角度(θ0)的规则波作用下开孔沉箱防波堤CR随波数的变化 Fig. 7 Variations in CR of perforated caisson breakwater versus k0d1 under the action of regular wave with different incident wave angle θ0 注: 计算条件: ε1=0.35, ε2=0.25, B1/d1=B2/d1=0.334, l/d1=1.26, d2/d1=0.54, d3/d1=0.18, H/d1=0.1 |
图 8给出规则波作用下双消浪室局部开孔沉箱防波堤反射系数CR随无因次波数k0d1的变化曲线。图中考虑了5种不同开孔率组合。共分为两类: 前后开孔墙开孔率相等时的计算结果, 曲线分别对应ε1=ε2=0.15, ε1=ε2=0.25和ε1=ε2=0.35的情况; 开孔率不相等时的计算结果, 即曲线对应前排开孔墙开孔率ε1小于(或大于)后墙开孔率的情况(ε1=0.25和ε2=0.35; ε1=0.35和ε2=0.25)。可以看出, 当前后开孔墙开孔率相同时, 随着开孔率的增大, 当0.6 < k0d < 1.75时, 双消浪室局部开孔沉箱防波堤反射系数CR明显减小, 防波堤消浪性能显著提升。当前墙开孔率大于后墙开孔率时(ε1=0.35和ε2=0.25), 防波堤在较大波频范围内反射系数较小。综合对比可以看出, 当前墙开孔率ε1大于后墙开孔率ε2时, 防波堤消浪效果明显好于其他组合(ε1=ε2或ε1 < ε2)的防波堤。
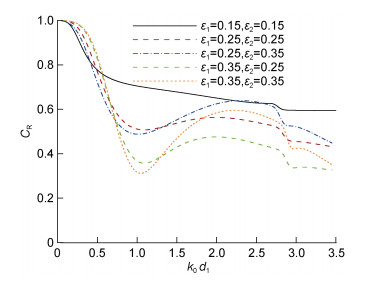 |
| 图 8 规则波作用下不同开孔率组合的防波堤反射系数CR随波数k0d1的变化 Fig. 8 Variations in CR of breakwater with different porosities versus k0d1 注: 计算条件: B1/d1=B2/d1=0.334, l/d1=1.26, H/d1=0.1, d2/d1=0.54, d3/d1=0.18, θ0=π/12 |
图 9给出了不规则波作用下防波堤反射系数CRir随波数ksd1变化的曲线, 其中ks=2π/Ls, Ls为有效波长。与图 8相同, 算例考虑了五种不同开孔率组合。可以看出, 在不规则波作用下, 当ε1=0.35和ε2=0.25以及ε1=ε2=0.35时, 双消浪室局部开孔沉箱防波堤反射系数CRir相对较小, 防波堤消浪效果较好。与图 8对比可发现, 不规则波作用下防波堤反射系数CRir随波数的变化与图 8中规则波作用下的反射系数变化趋势类似。考虑工程实际, 当开孔率较小时, 经过合理设计可以有效提高开孔墙的结构强度。如果同时考虑开孔沉箱的消波性能和结构强度, 推荐防波堤两排开孔墙开孔率组合为ε1=0.35和ε2=0.25。
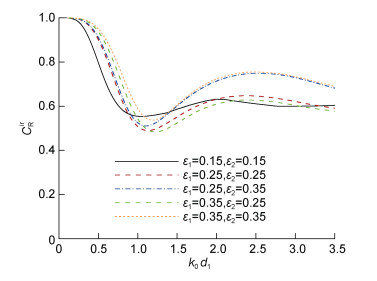 |
| 图 9 不规则波作用下不同开孔率组合的防波堤反射系数CRir随波数ksd1的变化 Fig. 9 Variations in CRir of breakwater with different porosities versus ksd1 under the action of irregular wave 注: 计算条件: B1/d1=B2/d1=0.334, l/d1=1.26, Hs/d1=0.1, d2/d1=0.54, d3/d1=0.18, θ0=π/12 |
基于势流理论, 本文利用匹配特征函数展开法建立了规则波和不规则波对双消浪室局部开孔沉箱防波堤作用的三维理论解。采用二次压力损失边界条件来考虑开孔墙对波浪运动的影响, 并引入周期性边界条件考虑开孔沉箱防波堤结构沿长度方向的周期性变化。通过计算分析验证了理论解和迭代过程的收敛性, 并开展相应物理模型试验验证本文理论模型的合理性。本文理论解能够合理预测双消浪室局部开孔沉箱防波堤的反射系数, 可以为工程初步设计提供重要参考。
通过算例分析发现: 双消浪室局部开孔沉箱防波堤结构在轴线方向呈周期性排列, 这导致堤前会发生波浪的漫反射现象。由于波浪漫反射的发生, 反射系数会在特定波频处发生突变, 而且随着入射角度的增大, 反射系数突变时的波数k0d1变小; 随着θ0从0增大到π/3, 反射系数减小, 随着波浪入射角度的继续增大, 反射系数增大明显; 随着波数的增大, 双消浪室局部开孔沉箱防波堤的反射系数先减小到最小值, 然后迅速增大。当前后开孔墙的开孔率相等时, 防波堤反射系数极小值随着开孔率的增大而减小。当沉箱前墙开孔率大于后墙开孔率时, 防波堤可有效减小波浪反射, 消浪效果显著。在本文计算条件下, 综合兼顾在较大频域内结构的消浪性能和开孔墙结构强度, 推荐双消浪室局部开孔沉箱相对消浪室宽度(B1+B2)/L取值为0.08~0.20; 推荐防波堤前后墙开孔率组合为ε1=0.35和ε2=0.25。
附录: 速度势中未知展开系数的求解在区域I和区域II交界面x=−B1处, 速度势满足速度连续和二次压力损失边界条件
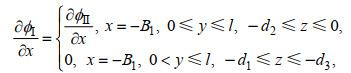 (A1)
(A1)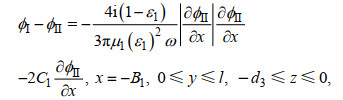 (A2)
(A2)区域II和区域III交界面x=0处, 速度势满足速度连续和二次压力损失边界条件
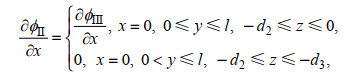 (A3)
(A3)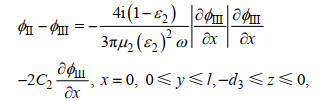 (A4)
(A4)其中, 下标1和2分别对应前和后开孔墙处的计算参数。
将式(16)和(17)代入式(A1), 然后在公式两侧乘以特征函数Ek*和Zp(z), 沿y方向从0到l积分, 沿z方向从−d1到0积分, 利用正交关系式, 并截断m和n到M项, j到N, k和i到±N, 可得
 (A5)
(A5)其中, 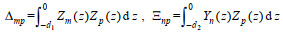
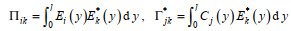
采用类似式(A1)中的处理方法匹配速度连续条件(A3)和二次压力损失边界条件(A2)和(A4), 可得到三组代数方程, 式(A2)、(A3)和(A4)可分别简化为
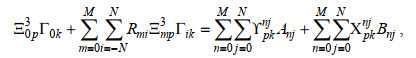 (A6)
(A6)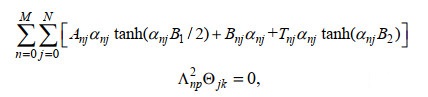 (A7)
(A7)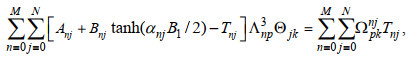 (A8)
(A8)其中, p=0, 1, …M、k=0, 1, …, N; 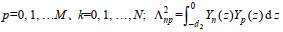
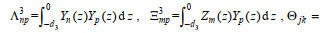
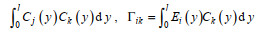
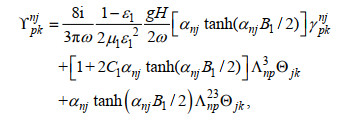 (A9)
(A9) (A10)
(A10)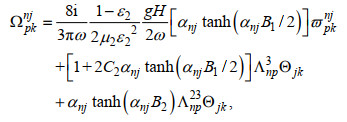 (A11)
(A11)其中, 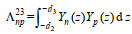
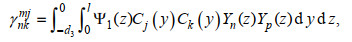
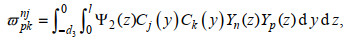
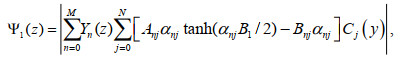
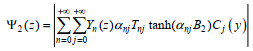
孙昭晨, 王利生, 1999. 斜向入射波与反射波的分离. 海洋学报, 21(4): 114-120 |
李玉成, 刘洪杰, 董国海, 2004. 局部开孔防波堤对斜向波反射的理论分析和试验研究. 水利学报, 35(10): 63-70 DOI:10.3321/j.issn:0559-9350.2004.10.010 |
俞聿修, 2006. 随机波浪及其工程应用. 大连: 大连理工大学出版社
|
BENNETT G S, MCIVER P, SMALLMAN J V, 1992. A mathematical model of a slotted wavescreen breakwater. Coastal Engineering, 18(3/4): 231-249 |
CHWANG A T, DONG Z, 1984. Wave-trapping due to a porous plate [C] // Proceedings of the 15th Symposium on Naval Hydrodynamics. Washington: National Academy Press: 407-417.
|
EVANS D V, FERNYHOUGH M, 1995. Edge waves along periodic coastlines. Part 2. Journal of Fluid Mechanics, 297: 307-325 DOI:10.1017/S0022112095003119 |
FERNYHOUGH M, EVANS D V, 1995. Scattering by periodic array of rectangular blocks. Journal of Fluid Mechanics, 305: 263-279 DOI:10.1017/S0022112095004629 |
GODA Y, 1999. A comparative review on the functional forms of directional wave spectrum. Coastal Engineering Journal, 41(1): 1-20 DOI:10.1142/S0578563499000024 |
HUANG Z H, 2006. A method to study interactions between narrow-banded random waves and multi-chamber perforated structures. Acta Mechanica Sinica, 22(4): 285-292 DOI:10.1007/s10409-006-0021-x |
HUANG Z H, LI Y C, LIU Y, 2011. Hydraulic performance and wave loadings of perforated/slotted coastal structures: a review. Ocean Engineering, 38(10): 1031-1053 DOI:10.1016/j.oceaneng.2011.03.002 |
JACOBSEN N G, VAN GENT M R A, WOLTERS G, 2015. Numerical analysis of the interaction of irregular waves with two dimensional permeable coastal structures. Coastal Engineering, 102: 13-29 DOI:10.1016/j.coastaleng.2015.05.004 |
JARLAN G E, 1961. A perforated vertical wall breakwater. The Dock and Harbour Authority, 41: 394-398 |
KONDO H, 1979. Analysis of breakwaters having two porous walls [C] // Proceedings Coastal Structures'79. Alexandria, VA, USA: ASCE: 962-977.
|
LEE J I, SHIN S, 2014. Experimental study on the wave reflection of partially perforated wall caissons with single and double chambers. Ocean Engineering, 91: 1-10 DOI:10.1016/j.oceaneng.2014.08.008 |
LINTON C M, MCIVER P, 2001. Handbook of Mathematical Techniques for Wave/Structure Interactions [M]. Boca Raton, Fla, USA: Chapman & Hall/CRC.
|
LIU Y, LI H J, 2017. Iterative multi-domain BEM solution for water wave reflection by perforated caisson breakwaters. Engineering Analysis with Boundary Elements, 77: 70-80 DOI:10.1016/j.enganabound.2016.12.011 |
LIU Y, LI Y C, TENG B, 2007. The reflection of oblique waves by an infinite number of partially perforated caissons. Ocean Engineering, 34(14/15): 1965-1976 |
LIU Y, LI Y C, TENG B, 2012. Interaction between obliquely incident waves and an infinite array of multi-chamber perforated caissons. Journal of Engineering Mathematics, 74(1): 1-18 DOI:10.1007/s10665-011-9484-2 |
LIU Y, LI Y C, TENG B, 2016. Interaction between oblique waves and perforated caisson breakwaters with perforated partition walls. European Journal of Mechanics - B/Fluids, 56: 143-155 DOI:10.1016/j.euromechflu.2015.12.001 |
LIU X, LIU Y, LI H J, et al, 2018. Experimental study of mean overtopping discharge at perforated caissons for non-impulsive waves. Science China Technological Sciences, 61(5): 711-723 DOI:10.1007/s11431-017-9206-5 |
MOLIN B, 2011. Hydrodynamic modeling of perforated structures. Applied Ocean Research, 33(1): 1-11 DOI:10.1016/j.apor.2010.11.003 |
MOLIN B, REMY F, 2013. Experimental and numerical study of the sloshing motion in a rectangular tank with a perforated screen. Journal of Fluids and Structures, 43: 463-480 DOI:10.1016/j.jfluidstructs.2013.10.001 |
PORTER R, EVANS D V, 2005. Embedded Rayleigh–Bloch surface waves along periodic rectangular arrays. Wave Motion, 43(1): 29-50 DOI:10.1016/j.wavemoti.2005.05.005 |
SAMMARCO P, DE FINIS S, CECIONI C, et al, 2021. ARPEC: a novel staggered perforated permeable caisson breakwater for wave absorption and harbour flushing. Coastal Engineering, 169: 103971 DOI:10.1016/j.coastaleng.2021.103971 |
SAWARAGI T, IWATA K, 1978. Wave attenuation of a vertical breakwater with two air chambers. Coastal Engineering in Japan, 21(1): 63-74 DOI:10.1080/05785634.1978.11924265 |
SUH K D, CHOI J C, KIM B H, et al, 2001. Reflection of irregular waves from perforated-wall caisson breakwaters. Coastal Engineering, 44(2): 141-151 |
SUH K D, PARK W S, 1995. Wave reflection from perforated-wall caisson breakwaters. Coastal Engineering, 26(3/4): 177-193 |
SUH K D, SHIN S, COX D T, et al, 2006. Hydrodynamic characteristics of pile supported vertical wall breakwaters. Journal of Waterway, Port, Coastal, and Ocean Engineering, 132(2): 83-96 DOI:10.1061/(ASCE)0733-950X(2006)132:2(83) |
SUH K D, SON S Y, LEE J I, et al, 2002. Calculation of irregular wave reflection from perforated-wall caisson breakwaters using a regular wave model [C] // 28th International Conference on Coastal Engineering 2002. Cardiff, Wales: World Scientific: 1709-1721.
|
TANIMOTO K, YOSHIMOTO Y, 1982. Theoretical and experimental study of reflection coefficient for wave dissipating caisson with a permeable front wall. Report of the Port and Harbour Research Institute, 21(3): 43-77 |
TENG B, ZHANG X T, NING D Z, 2004. Interaction of oblique waves with infinite number of perforated caissons. Ocean Engineering, 31(5/6): 615-632 |
WANG X Y, LIU Y, LU L, 2019. Analytical solution of oblique wave interacting with a periodic array of specific caissons connected with partially immersed thin walls (comb-type). Ocean Engineering, 186: 106107 |
WANG X Y, LIU Y, LU L, 2021. Analysis of oblique wave interaction with perforated caisson breakwaters with partial wave absorption parts. Ocean Engineering, 241: 110018 |
ZHAO Y, LIU Y, LI H J, 2020. Iterative analytical solution for wave reflection by a multi-chamber partially perforated caisson breakwater. Acta Oceanologica Sinica, 39(7): 115-126 |
ZHU S T, CHWANG A T, 2001. Investigations on the reflection behaviour of a slotted seawall. Coastal Engineering, 43(2): 93-104 |
 2022, Vol. 53
2022, Vol. 53


