中国海洋湖沼学会主办。
文章信息
- 张娜, 王立涛, 耿姗姗, 张庆河, 尤再进, 李帅, 许宁, 许钊. 2022.
- ZHANG Na, WANG Li-Tao, GENG Shan-Shan, ZHANG Qing-He, YOU Zai-Jin, LI Shuai, XU Ning, XU Zhao. 2022.
- 渤海海域冰水共存期的波能流密度推算
- ESTIMATION OF WAVE ENERGY FLUX DURING ICE WATER COEXISTENCE IN THE BOHAI SEA
- 海洋与湖沼, 53(4): 981-989
- Oceanologia et Limnologia Sinica, 53(4): 981-989.
- http://dx.doi.org/10.11693/hyhz20210700159
文章历史
-
收稿日期:2021-07-09
收修改稿日期:2021-09-19
2. 天津大学 水利工程仿真与安全国家重点实验室 天津 300072;
3. 国家海洋信息中心 天津 300171;
4. 大连海事大学 港口与航运安全协创中心 辽宁大连 116026;
5. 国家海洋环境监测中心 辽宁大连 116023
2. State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China;
3. National Marine Data and Information Service, Tianjin 300171, China;
4. Centre for Ports and Maritime Safety, Dalian Maritime University, Dalian 116026;
5. National Marine Environmental Monitoring Center, Dalian 116023, China
波浪能是一种可再生的清洁无污染能源, 其开发利用对于缓解不可再生能源危机和减少由化石燃料导致的环境污染具有重要意义(Borthwick, 2016)。波浪能是指海面上波浪的动能和势能, 主要是由风吹过海面引起的(尤再进等, 2017)。波浪能与波高的平方以及周期成正比。波浪能应用范围广泛, 已实现的用途有发电、取水、供热、海水淡化和制氢等(Wang et al, 2011; Ning et al, 2016; 王鑫等, 2020)。
我国的渤海海域受季风影响, 以风浪为主, 波高分布具有明显的季节性变化特征(郑崇伟等, 2013), 波能流密度的分布与有效波高相似, 均是秋冬大, 春夏小(郑崇伟等, 2013; 姜波等, 2017)。以往的研究表明, 渤海中部海域的波能流密度最大, 春季为1.6~ 2.4 kW/m, 夏季为0.7~1.4 kW/m, 秋季为2.4~ 3.4 kW/m, 冬季为4.2~5.4 kW/m (郑崇伟, 2014; 姜波等, 2017)。由此可见, 渤海波浪能最大的季节为冬季(万勇等, 2014), 然而冬季受西伯利亚强寒潮影响时, 一方面会导致风浪较大(郑崇伟, 2014), 另一方面又会导致海水结冰(Zhang et al, 2019, 2020), 海冰的形成会隔绝海-气交换, 导致波浪能的减弱(Zhang et al, 2019, 2020; 张娜等, 2021)。
渤海位于37°~41°N, 是北半球最南端的季节性海冰区(Zhang et al, 2019)。同时, 海冰已成为冬季影响渤海的主要海洋灾害之一(武浩等, 2016)。渤海的初冰日一般为12月上旬, 海冰首先出现在辽东湾近岸, 随后沿西海岸由北向南蔓延到渤海湾, 最后到达莱州湾, 于来年1、2月达到顶峰。其后春季来临, 气温升高, 海冰逐渐向北消融, 终冰日一般为3月中旬(Zhang et al, 2019)。渤海海冰主要集中在辽东湾、莱州湾和渤海湾地区, 海冰的覆盖率随离岸距离的增加而降低(Zhang et al, 2016, 2018)。我国渤海的单层平整冰的最大厚度通常不超过60 cm (白珊等, 1999)。辽东湾作为渤海海域冰情最严重的海域, 在重冰年冰厚一般为25~40 cm (白珊等, 1999)。以往针对渤海波浪能的研究大多没有考虑冬季海冰的影响。根据Zhang等(2020)的研究, 忽略海冰的影响会导致渤海波能流密度的高估, 而这种高估会严重误导电厂的选址。因此, 考虑海冰存在以准确估算渤海冬季波能流密度, 有待进一步研究。
以往的研究表明波流耦合模型能够有效提高近岸水域风浪计算精度与浅水水域波浪模拟精度(夏波等, 2013)。为了模拟更接近实际冰水共存海域动力环境的波浪演化过程, 本课题在Chen等(2018)前期工作的基础上, 采用MCT (model coupling toolkit)耦合器将FVCOM (finite-volume community ocean model)水动力学模型、海冰模型与SWAN (simulating wave nearshore)波浪模型实时耦合, 并在此基础上研究寒潮大风过程中渤海海冰对波浪模拟的影响, 从而实现冰水共存海域下波能流密度的准确评估。
1 数值模型本文采用非结构化网格有限体积法的海洋模型FVCOM (finite-volume community ocean model)模拟渤海海冰(Chen et al, 2003)。该模型包括水动力学模块和非结构化网格的海冰模块, 其中水动力学模块涉及到潮、流、海温和盐度方程的求解, 海冰模块的求解涉及到海冰热力学、动力学、传输以及本构方程的求解(Chen et al, 2003; Gao et al, 2011; 张庆河等, 2013)。波浪的模拟采用第三代风浪模式SWAN (simulating wave nearshore), 版本号为41.01 (the SWAN Team, 2018)。SWAN模型是基于包含源汇项的动谱平衡方程描述风浪生成及其在近岸区的演化过程, 具体方程描述参见文献(Booij et al, 1999)。
1.1 海冰模型-水动力学模型-波浪模型的耦合原理本文在Chen等(2018)的波流耦合系统的基础上基于MCT (model coupling toolkit)耦合器建立了海冰模型-水动力学模型-波浪模型的实时耦合模式。MCT耦合器是一套能够使独立的模型实现互相耦合的开源程序工具包, 它采用Fortran90进行编写, 能够支持串行和基于MPI (message passing interface)的并行运算。MCT耦合器能够为每个模型分配系统工作进程, 各子模型通过调用MCT模块实现变量传递。MCT耦合器的具体描述参见文献(Warner et al, 2008)。
耦合模型包括FVCOM水动力学模型、海冰模型和SWAN波浪模型, 由主程序调用各子模型同时独立运行, 当达到用户设定的数据交换时间时, 各子模型通过MCT耦合器进行实时变量交换, 交换结束后, 各子模式继续进行运算, 循环进行直至达到用户设定的结束时间, 结束运算。FVCOM水动力学模型、海冰模型与SWAN波浪模型采用了相同的非结构化三角形网格, 不需进行插值计算。
海冰模型-水动力学模型-波浪模型耦合模式之间的变量交换为: (1) 水动力学模型中的潮位(Elev)、垂向平均流速分量(Ua、Va); (2) 海冰模型中的海冰浓度(Aice); (3) SWAN中的波长(L)、波向(Dir)、有效波高(Hs)、谱峰波周期(Tp)、平均波周期(T01)、底部波周期(Tbot)以及底部波动轨迹速度(Ubot), 如图 1所示。
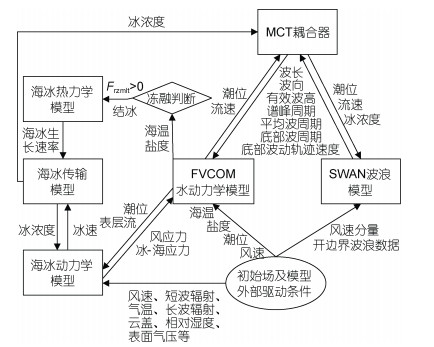 |
| 图 1 耦合流程及变量关系传递图 Fig. 1 Model coupling process and its variable transfer 注: Frzmlt为海水结冰的判定条件, 当Frzmlt > 0时即认为海水开始结冰 |
当达到用户设定的交换时间时, 海冰模型将模拟得到的海冰浓度与水动力学模型计算得到的潮位和垂向平均的流速分量传递给MCT耦合器, 由MCT耦合器将这些变量传递给SWAN波浪模型, 以此考虑潮流和海冰对波浪场的影响。同时FVCOM水动力学模型通过MCT耦合器接收SWAN波浪模型计算得到的包含冰影响的波长、波向、有效波高、谱峰波周期、平均波周期、底部波周期以及底部波动轨迹速度, 从而计算出新的潮位和流速传输给海冰模型用于计算新的冰浓度, 而新的冰浓度与新的潮位和流速又用于传输给SWAN波浪模型, 从而实现海冰模型-水动力学模型-波浪模型的耦合。当达到用户设定的结束时间时, 计算终止。
在冬季, 渤海海域寒潮大风频发, 强风是浪的主要驱动条件。在寒潮大风期间, 低气温导致海水结冰, 而海冰的出现会影响大气与海表面之间的动量交换, 从而影响了风浪的形成。根据Connolley等(2004)的结果, 在冰水共存的海域中, 海表面风应力可利用冰浓度的线性修正函数表示。因此本文将海冰模型和水动力学模型耦合模拟得到的冰浓度Aice作为海表面应力的一部分, 以线性变化加权百分比的方式纳入SWAN模型的海面摩阻风速方程中, 用于模拟冰水共存条件下的波浪演化过程。在冰水共存海域的波浪模型中, 海面摩阻风速Ufric的表达式被改写为:
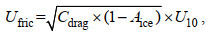 (1)
(1)式中, Cdrag为风拖曳力系数(Wu, 1982); Aice为冰浓度, 由FVCOM模型的海冰模块计算输出(Thorndike et al, 1975); U10为10 m高度处的风速。根据式(1)计算出的海面摩阻风速计算JONSWAP (joint North Sea wave project)谱; 接着再输入谱峰波周期对应的频率计算出当前时刻下的作用密度, 进而得到波能密度的零阶矩, 最终得到考虑冰影响的波浪参数。
1.3 波能流密度的计算公式单位时间内波浪在传播方向上通过单位波峰宽度上的能量被定义为波能流密度, 用P表示, 单位为kW/m。由定义可得, 波能流密度的计算公式(2)可写为(Brooke, 2003):
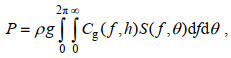 (2)
(2)式中, ρ为海水密度; g为重力加速度; Cg (f, h)为波群速度; S(f, θ)为波浪谱能量密度; f为波浪频率; h为水深; θ为波的传播方向。
有效波高(Ochi, 1998)通常定义为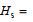
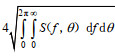
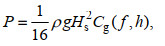 (3)
(3)式中, 波群速度Cg(f, h)与水深h有关(Barbariol et al, 2013):
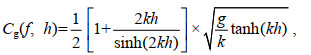 (4)
(4)k为频率, 对应波数为(Dean et al, 1991)
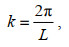 (5)
(5)或者
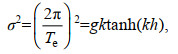 (6)
(6)式中, L为波长; σ为波的角频率; Te为波能量周期。
结合公式(4)~(6), Cg(f, h)波群速度可以表示为(Liang et al, 2017)
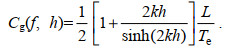 (7)
(7)结合公式(3)和公式(7), 波能流密度公式可以进一步表示为
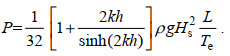 (8)
(8)对于深水区(kh > π, 也即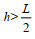
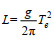
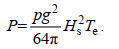 (9)
(9)FVCOM模型的输入数据包括气象数据(如气温、风、相对湿度、气压、云盖、短波辐射、长波辐射等)、开边界的驱动数据(如潮、海温等)以及初始场数据(海温、盐度)。SWAN模型的输入数据为10 m高度处的风和波浪开边界。
气象数据来自美国国家环境预报中心(National Centers for Environmental Prediction, NCEP), 其时间和空间分辨率分别为1 h和0.2° (Saha et al, 2010)。FVCOM模型的开边界潮位数据来自Chinatide (李孟国等, 2007), 开边界和初始场的海温和盐度数据来自HYCOM (HYbrid coordinate ocean model) (Chassignet et al, 2007)。SWAN模型的开边界波浪数据由第五代欧洲中期天气预报中心ECMWF (European Centre for Medium-range Weather Forecasts)再分析数据提供, 时间分辨率为1 h, 空间分辨率为0.5° (Hersbach et al, 2016)。以往的研究表明, 以上数据与实测值吻合较好, 能够为数值模拟提供合理的模型驱动条件(Zhang et al, 2020)。
地形水深来自渤海1︰15万海图地理信息系统数据(1999年), 结合近岸较高分辨率的海图数据以及实测地形数据加密, 最小空间分辨率为800 m, 如图 2所示。
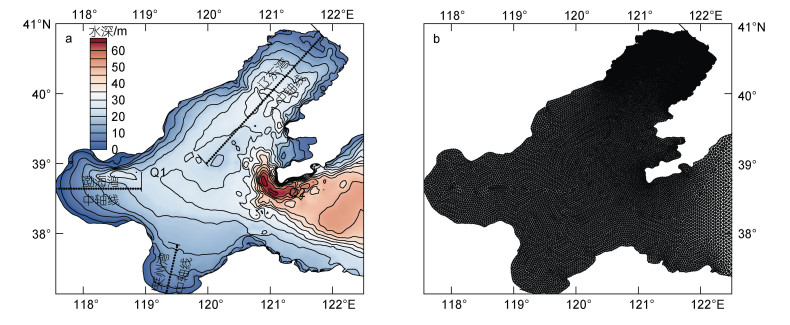 |
| 图 2 渤海水深(a)与网格划分(b) Fig. 2 Water depth (a) and grid (b) in the Bohai Sea 注: Q1和Q2分别表示位于渤海湾和老铁山水道的观测点 |
模型验证包括海冰和波浪两部分。海冰验证资料采用MODIS (moderate-resolution imaging spectroradiometer)卫星遥感图像, 波浪验证基于全国海洋立体观测网中的浮标观测波浪资料。
2.1 海冰模型验证2012年2月8日, 渤海海冰覆盖范围最大, 模拟的渤海海冰面积约为29.79×103 km2, 其中辽东湾占比71.1%, 渤海湾占比22.3%, 莱州湾占比6.6%。模拟的渤海海冰面积占整个渤海面积的30%, 比MODIS的海冰面积偏小1.2%。渤海湾、辽东湾和莱州湾数值模拟的海冰分布及最大离岸距离与卫星遥感图像基本一致, 如图 3所示。
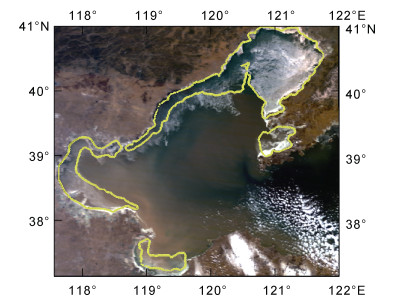 |
| 图 3 渤海海冰数值模拟结果与MODIS卫星遥感图像对比 Fig. 3 Comparison between sea ice numerical simulation result and MODIS satellite remote sensing image of the Bohai Sea 注: 黄色线为数值模拟的海冰轮廓线 |
波浪模拟结果的验证取自2012年2月5~8日的一个寒潮大风过程, 受低气温影响, 此时渤海海冰达到年度最大值。如图 4所示, 2月6~8日期间, 实测日最大风速在14.4~15.0 m/s之间, 风向为NE和NW向。波浪模拟结果验证包括以下2种。(1) 不考虑海冰影响的波浪模拟结果; (2) 通过海冰模型-水动力学模型-波浪模型实时耦合模拟得到的波浪结果。从图 4中可以看出, 第2种实时耦合模式模拟得到的有效波高值与实测值最为接近, 尤其是最大值几乎与实测值吻合。第1种无冰影响的有效波高模拟值在大风期间要远远大于实测值, 最大有效波高比实测值偏大15%。大风期间不考虑海冰影响的有效波高模拟值与实测值的平均相对误差是实时耦合模式的1.7倍。
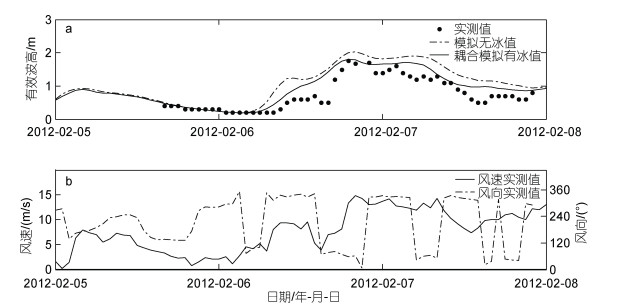 |
| 图 4 实时耦合模式模拟的渤海湾Q1点(119.0°E, 38.9°N)的有效波高与不考虑海冰影响的模拟值及实测值的对比 Fig. 4 Comparison between significant wave heights simulated by real-time coupled model with sea ice without sea ice and the measured values at point Q1 (119.0°E, 38.9°N) in Bohai Bay |
2012年2月5日至8日, 渤海最低气温为−24℃, 平均气温为−20 ℃。渤海三个湾均被海冰覆盖, 分布范围达到最大值。从图 5可知, 2012年2月5~8日, 辽东湾近岸的海冰出现概率最大高达95%, 渤海湾近岸的海冰出现概率最大为50%, 而莱州湾的海冰出现概率最大为40%, 结冰区域面积占到了渤海总面积的三分之一。
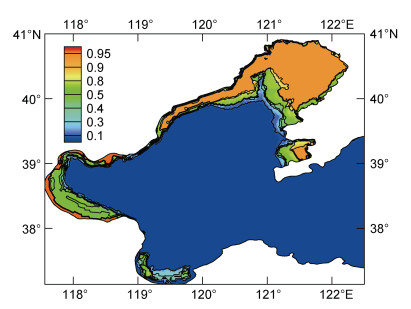 |
| 图 5 2012年2月5~8日渤海海冰出现概率分布 Fig. 5 Probability of sea ice occurrence in the Bohai Sea from Feb. 5 to 8, 2012 |
根据图 6, 2012年2月5日0时至2012年2月8日0时, 在考虑海冰影响的情况下, 辽东湾、渤海湾和莱州湾平均波能流密度的最大值分别为5.9, 6.1和5.6 kW/m, 分别位于各自的湾口位置处, 比不考虑海冰影响时分别减小了10.6%、1.6%和1.8%。辽东湾、渤海湾和莱州湾近岸区域的平均波能流密度较不考虑海冰影响时最多分别减少了100%、60%和50%, 见表 1。
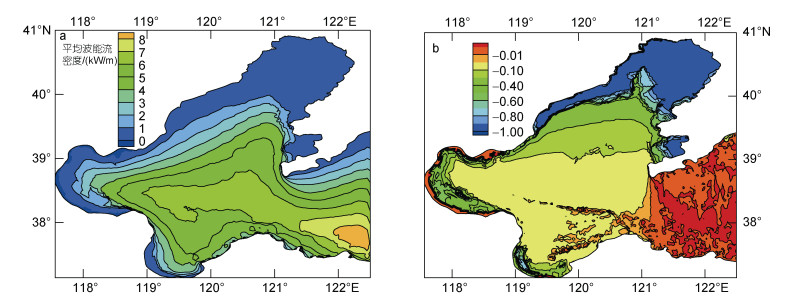 |
| 图 6 2012年2月5日至8日渤海考虑海冰影响的平均波能流密度(a)和受海冰影响的程度(b) Fig. 6 Average wave energy flux with sea ice effect (a) and the influence of sea ice (b) in the Bohai Sea from Feb. 5 to 8, 2012 |
| 统计内容 | 辽东湾 | 渤海湾 | 莱州湾 |
| 受冰影响区域占比 | 100% | 100% | 100% |
| 受冰影响最大程度 | −100% | −60% | −50% |
为了深入研究海水结冰对渤海三个湾波能流密度的影响, 图 7给出了渤海各湾中轴线处平均波能流密度受冰影响的程度, 中轴线位置见图 2a。2012年2月5日0时至2012年2月8日0时, 距辽东湾湾顶129.2 km是海冰沿中轴线处出现的最大离岸距离。其中沿辽东湾中轴线方向距湾顶78.2 km内, 海冰出现概率为95%, 其平均波能流密度受海冰影响最为严重, 减少了100%。而在距辽东湾顶78.2~129.2 km范围内, 随着海冰出现概率逐渐减小, 平均波能流密度受海冰影响的程度也越来越小, 从100%减小到32%。而在距辽东湾顶129.2~255.1 km范围内, 虽然没有海冰覆盖, 但平均波能流密度仍然受海冰影响而减小, 减小程度从32%到10%。这主要是由于海冰的出现阻隔了海-气之间的热量和动量交换, 相当于减小了渤海的有效风区, 从而使得无冰海域的平均波能流密度也会减小。
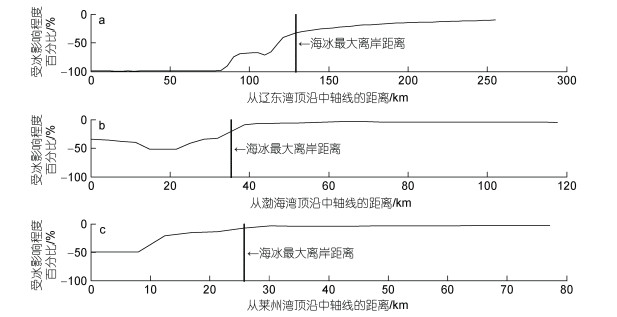 |
| 图 7 渤海各湾中轴线处平均波能流密度受冰影响的程度 Fig. 7 Effect of sea ice on average wave energy flux at central axis of each bay of the Bohai Sea 注: a: 辽东湾; b: 渤海湾; c: 莱州湾 |
2012年2月5日0时至2012年2月8日0时, 渤海湾沿着中轴线距离湾顶的海冰最大覆盖范围为35.3 km, 其中距离湾顶21.6 km范围内的平均波能流密度受海冰影响最为严重, 最大减少了52%。在距渤海湾顶21.6~35.3 km范围内, 随着海冰出现概率的逐渐减小, 平均波能流密度受冰影响的减小程度从52%到21%。而在距渤海湾顶35.3~117.7 km范围内, 虽然没有海冰覆盖, 但平均波能流密度仍然受海冰影响而减小, 减小程度从21%到5%。
莱州湾与渤海湾情况类似。2012年2月5日0时至2012年2月8日0时, 莱州湾沿着中轴线距离湾顶的海冰最大覆盖范围为25.8 km, 在距湾顶8.0 km范围内, 平均波能流密度受海冰影响最为严重, 最大减少了50%。在距莱州湾顶8.0~25.8 km范围内, 随着海冰出现概率的逐渐减小, 平均波能流密度受冰影响的减小程度从50%到8%。而在距莱州湾顶25.8~77.1 km范围内, 虽然没有海冰覆盖, 但平均波能流密度仍然受海冰影响而减小, 减小程度从8%到3%。
3.3 无冰覆盖区域波能流密度随时间的演化渤海的海冰主要位于渤海湾, 辽东湾和莱州湾的近岸区域, 且辽东湾的冰情最重, 如图 3所示。海冰的存在阻隔了海-气之间的热量和动量交换, 减小了渤海的有效风区, 可能导致无冰海域的波能流密度减小。为了探讨无冰覆盖海域的波能流密度在考虑和不考虑海冰影响时随时间演化的规律, 挑选了2012年2月5日0时至2012年2月8日0时渤海海冰年度最大期间渤海湾Q1点与老铁山水道Q2点进行对比分析。这两个点在这段时间内均无海冰覆盖, 因此我们可以通过对比考虑和不考虑海冰影响两种情况下波能流密度随时间的演化进而判断海冰是否能通过减小有效风区(也即开阔水域)的占比而使得无冰区域的波能流密度减小。
在考虑海冰影响的情况下, 位于渤海湾Q1点的波能流密度在2012年2月5日0时至2012年2月8日0时的平均值为2.5 kW/m, 比不考虑海冰影响时减小了24%, 最大值为8.4 kW/m, 比不考虑海冰影响时减小了18%, 如图 8a所示。老铁山水道Q2点在考虑海冰影响下的波能流密度平均值为4.3 kW/m, 比不考虑海冰影响时减小了19%; 最大值为15.4 kW/m, 比不考虑海冰影响时减小了14%, 如图 8b所示。其中, 从2月5日0时至2月6日7时期间平均风速约为4.0 m/s, 海冰对波能流密度的影响几乎可以忽略。在2月6日8时至2月8日0时期间, 平均风速为10.6 m/s, 在考虑海冰影响的情况下渤海湾Q1点的平均波能流密度为4.0 kW/m, 比不考虑海冰影响时减小了25%。老铁山水道Q2点的平均波能流密度为7.8 kW/m, 比不考虑海冰影响时减小了20%。由此可见在强风作用下海冰的消浪效果是十分显著的。
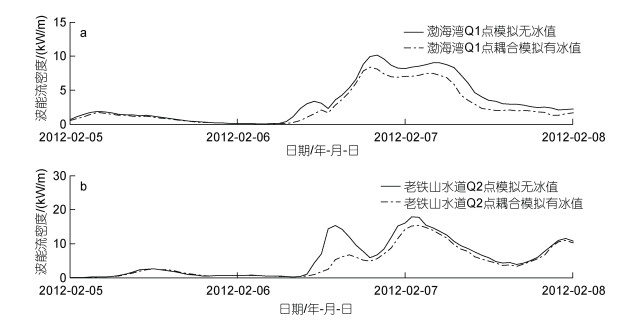 |
| 图 8 有无海冰影响的平均波能流密度随时间演化的对比 Fig. 8 Comparison in average wave energy flux of time series with and without sea ice effect 注: a: 渤海湾Q1点(119.0°E, 38.9°N); b: 老铁山水道Q2点(121.078°E, 38.617°N) |
与图 8a的渤海湾Q1点相比, 老铁山水道的波能流密度几乎是它的两倍, 即使是在海冰分布年度最大的时刻, 老铁山水道的波能流密度仍然更适合用于波能发电。
4 结语根据模型验证结果可知, 本文建立的海冰模型-水动力学模型-波浪模型的实时耦合模式能够较好地模拟渤海冬季寒潮大风期间的海冰及波能流密度的分布。根据模拟结果可知, 寒潮大风期间渤海约1/3的海域被海冰覆盖, 然而其平均波能流密度受冰影响的区域占整个渤海的76%, 辽东湾、渤海湾和莱州湾的平均波能流密度受冰影响最多分别减小了100%, 60%和50%。
老铁山水道虽然冬季不结冰, 但在寒潮大风期间, 波能流密度的平均值仍然比不考虑海冰影响时减小了19%。这说明海水结冰不仅导致结冰区域的有效波高和波能流密度会受到海冰影响而减小, 也会导致不结冰海域的有效风区(开阔水域面积)减小, 从而造成不结冰海域的波能流密度减小。此外, 老铁山水道的波能流密度几乎是渤海湾口的两倍, 即使是在海冰严重的时期, 其波能流密度仍然符合发电需求。
万勇, 张杰, 孟俊敏, 等, 2014. 基于ERA-Interim再分析数据的OE-W01区块波浪能资源评估. 资源科学, 36(6): 1278-1287 |
王鑫, 李大鸣, 王兵振, 等, 2020. 点吸收式波浪能俘获装置结构优化方法研究. 海洋与湖沼, 51(2): 293-297 |
尤再进, 尹宝树, 石洪源, 2017. 应用"跨零-能量"法估算海洋波浪再生能资源. 海洋与湖沼, 48(5): 926-931 |
白珊, 刘钦政, 李海, 等, 1999. 渤海的海冰. 海洋预报, (3): 1-9 |
李孟国, 郑敬云, 2007. 中国海域潮汐预报软件Chinatide的应用. 水道港口, 28(1): 65-68 DOI:10.3969/j.issn.1005-8443.2007.01.015 |
张娜, 李帅, 耿姗姗, 等, 2021. 渤海海冰对波浪推算的影响. 哈尔滨工程大学学报, 42(11): 1231-1237 |
张庆河, 张娜, 2013. 渤海海冰演化的三维数值模型. 天津大学学报, 46(4): 333-341 |
武浩, 夏芸, 许映军, 等, 2016. 2004年以来中国渤海海冰灾害时空特征分析. 自然灾害学报, 25(5): 81-87 |
郑崇伟, 2014. 利用WW3模式实现中国周边海域波浪能流密度数值预报——以2次冷空气过程为例. 亚热带资源与环境学报, 9(2): 18-25 DOI:10.3969/j.issn.1673-7105.2014.02.004 |
郑崇伟, 苏勤, 刘铁军, 2013. 1988-2010年中国海域波浪能资源模拟及优势区域划分. 海洋学报, 35(3): 104-111 DOI:10.3969/j.issn.0253-4193.2013.03.012 |
姜波, 丁杰, 武贺, 等, 2017. 渤海、黄海、东海波浪能资源评估. 太阳能学报, 38(6): 1711-1716 |
夏波, 张庆河, 蒋昌波, 2013. 基于非结构网格的波流耦合数值模式研究. 海洋与湖沼, 44(6): 1451-1456 |
BARBARIOL F, BENETAZZO A, CARNIEL S, et al, 2013. Improving the assessment of wave energy resources by means of coupled wave-ocean numerical modeling. Renewable Energy, 60: 462-471 DOI:10.1016/j.renene.2013.05.043 |
BOOIJ N, RIS R C, HOLTHUIJSEN L H, 1999. A third- generation wave model for coastal regions: 1.Model description and validation. Journal of Geophysical Research: Oceans, 104(C4): 7649-7666 DOI:10.1029/98JC02622 |
BORTHWICK A G L, 2016. Marine renewable energy seascape. Engineering, 2(1): 69-78 DOI:10.1016/J.ENG.2016.01.011 |
BROOKE J, 2003. Wave Energy Conversion. Oxford, UK: Elsevier Science Ltd, 157-164
|
CHASSIGNET E P, HURLBURT H E, SMEDSTAD O M, et al, 2007. The HYCOM (HYbrid Coordinate Ocean Model) data assimilative system. Journal of Marine Systems, 65(1/4): 60-83 |
CHEN C S, LIU H D, BEARDSLEY R C, 2003. An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries. Journal of Atmospheric and Oceanic Technology, 20(1): 159-186 DOI:10.1175/1520-0426(2003)020<0159:AUGFVT>2.0.CO;2 |
CHEN T Q, ZHANG Q H, WU Y S, et al, 2018. Development of a wave-current model through coupling of FVCOM and SWAN. Ocean Engineering, 164: 443-454 DOI:10.1016/j.oceaneng.2018.06.062 |
CONNOLLEY W M, GREGORY J M, HUNKE E, et al, 2004. On the consistent scaling of terms in the sea-ice dynamics equation. Journal of Physical Oceanography, 34(7): 1776-1780 DOI:10.1175/1520-0485(2004)034<1776:OTCSOT>2.0.CO;2 |
DEAN R G, DALRYMPLE R A, 1991. Water Wave Mechanics for Engineers and Scientists. Teaneck, NJ: World Scientific Publishing Company, 55-61
|
GAO G P, CHEN C S, QI J H, et al, 2011. An unstructured-grid, finite-volume sea ice model: development, validation, and application. Journal of Geophysical Research: Oceans, 116(C8): C00D04 |
HERSBACH H, DEE D, 2016. ERA5 reanalysis is in production[J]. ECMWF Newsletter, 147: 7, https://www.ecmwf.int/en/elibrary/16299-newsletter-no-147-spring-2016.
|
LIANG B C, SHAO Z X, WU G X, et al, 2017. New equations of wave energy assessment accounting for the water depth. Applied Energy, 188: 130-139 DOI:10.1016/j.apenergy.2016.11.127 |
NING D Z, WANG R Q, ZOU Q P, et al, 2016. An experimental investigation of hydrodynamics of a fixed OWC Wave Energy Converter. Applied Energy, 168: 636-648 DOI:10.1016/j.apenergy.2016.01.107 |
OCHI M K, 1998. Ocean Waves: the Stochastic Approach. .Cambridge: Cambridge University Press, 92-95
|
SAHA S, MOORTHI S, PAN H L, et al, 2010. The NCEP climate forecast system reanalysis. Bulletin of the American Meteorological Society, 91(8): 1015-1058 DOI:10.1175/2010BAMS3001.1 |
THE SWAN TEAM, 2018. SWAN user manual[S]. SWAN cycle Ⅲ version 41.01. Delft, Netherlands: Delft University of Technology: 1-125, https://swanmodel.sourceforge.io/.
|
THORNDIKE A S, ROTHROCK D A, MAYKUT G A, et al, 1975. The thickness distribution of sea ice. Journal of Geophysical Research, 80(33): 4501-4513 DOI:10.1029/JC080i033p04501 |
WANG S J, YUAN P, LI D, et al, 2011. An overview of ocean renewable energy in China. Renewable and Sustainable Energy Reviews, 15(1): 91-111 |
WARNER J C, PERLIN N, SKYLLINGSTAD E D, 2008. Using the Model Coupling Toolkit to couple earth system models. Environmental Modelling & Software, 23(10/11): 1240-1249 |
WU J, 1982. Wind-stress coefficients over sea surface from breeze to hurricane. Journal of Geophysical Research: Oceans, 87(C12): 9704-9706 DOI:10.1029/JC087iC12p09704 |
ZHANG N, LI S, WU Y S, et al, 2020. Effects of sea ice on wave energy flux distribution in the Bohai Sea. Renewable Energy, 162: 2330-2343 |
ZHANG N, MA Y T, ZHANG Q H, 2018. Prediction of sea ice evolution in Liaodong Bay based on a back-propagation neural network model. Cold Regions Science and Technology, 145: 65-75 |
ZHANG N, WANG J, WU Y S, et al, 2019. A modelling study of ice effect on tidal damping in the Bohai Sea. Ocean Engineering, 173: 748-760 |
ZHANG N, WU Y S, ZHANG Q H, 2016. Forecasting the evolution of the sea ice in the Liaodong Bay using meteorological data. Cold Regions Science and Technology, 125: 21-30 |
 2022, Vol. 53
2022, Vol. 53


