中国海洋湖沼学会主办。
文章信息
- 李佳谦, 邵珠晓, 梁丙臣. 2022.
- LI Jia-Qian, SHAO Zhu-Xiao, LIANG Bing-Chen. 2022.
- 渤海和黄海北部波高与周期联合分析
- JOINT ANALYSIS OF WAVE HEIGHT AND WAVE PERIOD IN THE BOHAI SEA AND NORTHERN YELLOW SEA
- 海洋与湖沼, 53(4): 990-998
- Oceanologia et Limnologia Sinica, 53(4): 990-998.
- http://dx.doi.org/10.11693/hyhz20211200346
文章历史
-
收稿日期:2021-12-28
收修改稿日期:2022-03-12
海浪是自然界中最复杂易变的现象之一, 对于海洋工程以及很多海上活动而言, 分析海浪波高与周期的联合分布具有重要意义。波浪对于海洋工程建筑物的作用力取决于波高和周期的综合影响, 当波浪的周期与建筑物的自振周期接近时, 产生的共振现象对海洋工程建筑物是一种极大的安全威胁(文先华等, 2016)。渤海、黄海北部(简称黄渤海)地处温带, 是典型的半封闭陆架海域, 近十年来, 环渤海地区经济飞速发展, 该区域发展的重心为海洋资源的开发和海洋工业的发展(王立国等, 2012)。但黄渤海地处北半球高纬度地区, 时常遭受寒潮、台风等天气过程的侵害。因此深入研究分析黄渤海的年纪代波浪特征, 可以为该海域相关海洋工程的设计和防灾减灾提供参考和依据。
国内学者基于波浪实测数据、后报数据对中国海域的波浪特征已经进行了系列的研究。高晨晨等(2019)利用响水波浪站2011年的现场观测数据, 研究了波高和波周期的变化规律。潘冬冬等(2020)利用粤东近岸深水区2018年的波浪实测资料, 分析了该海域周年波浪的基本特征, 并深入研究了台风浪的波浪特征。范琳琳(2019)基于WAVEWATCH-Ⅲ数值后报数据, 分析了南海海域1989~2018年有效波高和平均波周期的时空分布和联合分布的特征。谢欣等(2019)利用福建外海海浪数值后报数据, 分析了该海域海浪波高和周期的统计特性, 提出了以波高和周期为双指标的海浪危险性分析方法。这些研究都通过不同海域的波浪数据对海浪的特征进行探讨, 并且较准确地描述了研究海域的波浪特征。然而, 目前关于黄渤海海域的长期波浪特征的分析较少, 主要是因为难以获得长期的实测波浪数据。
本文将利用1999~2018年SWAN模拟的海浪后报数据, 对渤海以及黄海北部区域海浪的波高和周期进行统计分析, 讨论该海域的波高分布特征、波周期分布特征及波高和周期的联合分布特征, 研究成果可为该地区沿海建筑物的设计以及防灾减灾提供参考和依据。
1 研究区域与波浪数据来源本文选择渤海及黄海北部海域为研究区域(图 1), 经度范围为117°~127°E, 纬度范围为35°~41°N。
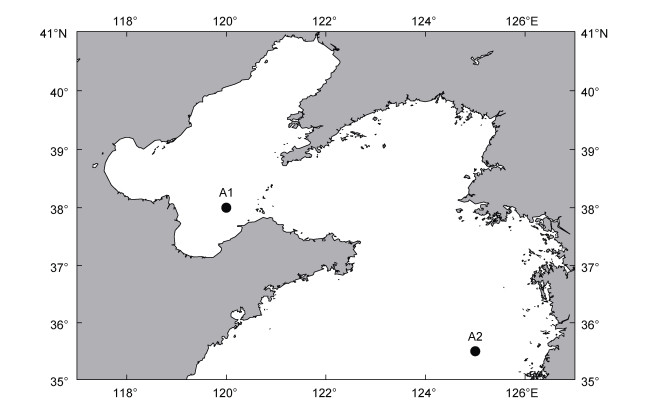 |
| 图 1 研究区域和研究点A1、A2 Fig. 1 Research area and site deployments |
由于波浪实测数据有限, 波浪模拟是在区域或全球尺度上提供高分辨率和长期波浪信息的一种替代工具(唐军等, 2008; Shi et al, 2019)。SWAN是一种基于能量平衡方程的波浪数学模型, 全面地考虑了多种物理过程, 包括风生浪、白帽耗散、底摩擦耗散、深致破碎、波-流相互作用、非线性波-波相互作用等(雷鹏等, 2019), 已经被较广泛地应用于波浪的数值模拟(丁磊等, 2020; 姬厚德等, 2021; 周昕伟等, 2021)。Shao等(2020)利用SWAN模型对1979~2018年中国近海的波浪场进行了数值模拟, 并将模拟的后报数据与浮标实测数据进行了对比分析, 模拟结果与实测波浪数据吻合较好, 于是建立了中国近海海浪后报数据库。本研究直接提取了数据库中渤海以及黄海北部区域1999~2018年海浪的后报数据为数据来源。后报数据的空间精度为0.1°, 时间步长为1 h。
2 渤海、黄海北部波高周期分布特征海浪波高和波周期的分析对海洋工程有着重要的影响, 特别是在荷载估算、设备调整、沙丘侵蚀以及波浪能开发(乔守文等, 2020; Gao et al, 2021)。本文利用从数据库提取得到的20年的后报数据, 对研究海域的波高和周期做多年的季节平均, 得到了波高和周期季节平均的分布图, 以波高, 春季为例, 它们是20年内春季所有空间记录的平均值。同时也获取了所有空间记录的20年波高和周期的最大值, 得到了最大值的分布图, 结果如下。
2.1 波高和周期的季节性分布特征分析图 2可得该海域有效波高季节性变化较为显著, 在冬季, 有效波高的平均值明显大于其他三个季节, 最大可达1.2 m, 主要原因为该区域台风发生次数较少, 主要受冬季风暴影响。有效波高季平均值的区域特征明显, 受水深影响, 有效波高在研究区域中间的深水区大于四周的近岸区, 并且呈现南向北递减的趋势, 在黄海北部深海区, 四个季节的有效波高平均值均大于1.0 m, 并且平均值的最大值均出现在(124°E, 35°N)附近; 在渤海海域, 四个季节的有效波高平均值均小于0.8 m, 夏季小于0.5 m。
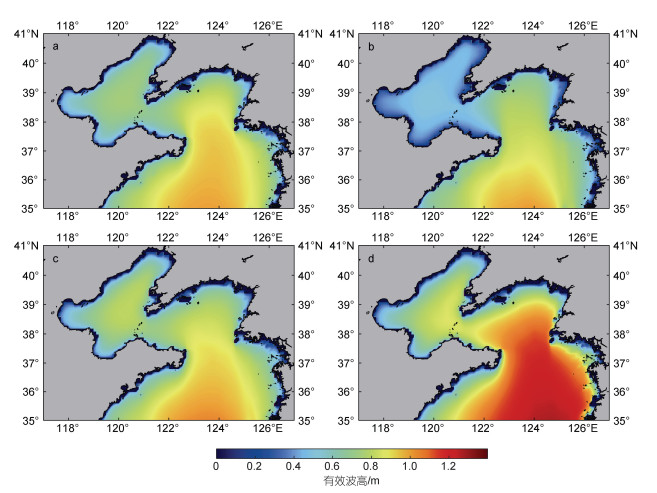 |
| 图 2 研究区域波高的季节平均值 Fig. 2 The seasonal mean of wave height in the research area 注: a. 春季; b. 夏季; c. 秋季; d. 冬季 |
由图 3可知, 波周期的季平均分布特征与有效波高的分布类似, 季节性特征较为显著, 在夏季, 波周期的平均值大于其他三个季节, 最大可达到7.8 s。波周期季平均值的区域特征较为明显, 呈现出由南向北递减的趋势, 在黄海北部深海区, 四个季节的波周期平均值均大于7 s; 在渤海海域, 波周期的季平均值均较小, 四季均不超过5 s。
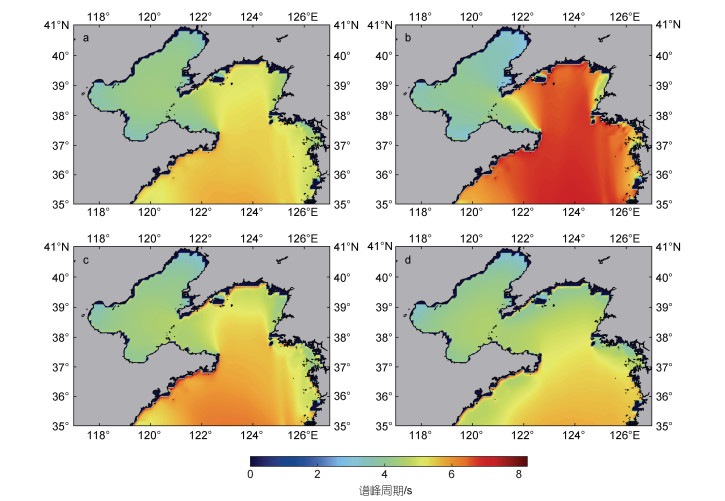 |
| 图 3 研究区域波周期的季节平均值 Fig. 3 The seasonal mean of wave period in the research area 注: a. 春季; b. 夏季; c. 秋季; d. 冬季 |
由图 4可知, 研究区域1999~2018年波高最大值区域性特征较为明显, 呈现由南向北逐渐减小的趋势, 黄海北部最大可达到8.75 m, 在渤海区域, 均小于5.5 m。同样, 受水深影响, 波高的最大值呈现由深海向近岸逐渐减小的趋势。
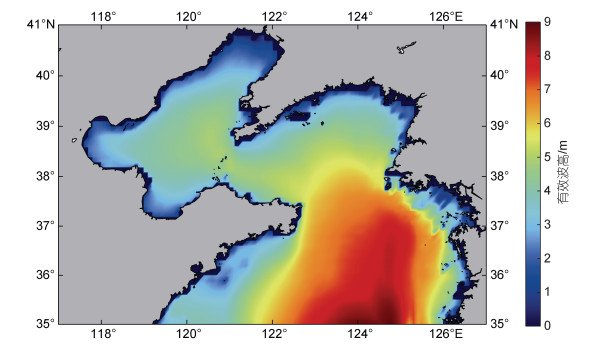 |
| 图 4 研究区域波高20年的最大值 Fig. 4 The maximum wave height of the 20 years in the research area |
图 5描绘了研究区域1999~2018年波周期最大值的分布特征, 与波高明显不同, 波周期最大值在整个研究区域均较大, 最大可达到19.5 s。
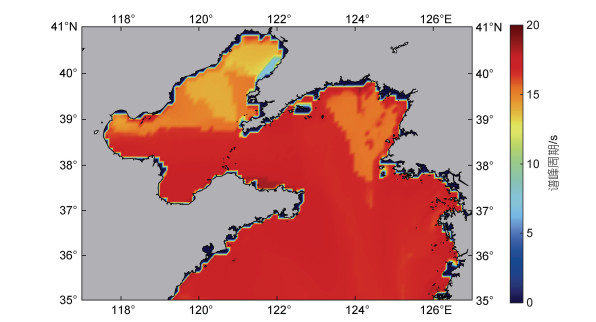 |
| 图 5 研究区域波周期20年的最大值 Fig. 5 The maximum wave period of the 20 years in the research area |
对于大多数波浪来说, 其波高和周期是相互关联, 因此研究海浪波高和周期的联合分布特征对海洋工程来说是非常重要的。当波高和周期不能保持维持其稳定所需要的平衡状态时, 波浪就会发生破碎。因此, 对于某个给定的海况来说, 波高和周期的联合分布对于波浪破碎概率的估计意义重大。同时海浪的波高和周期联合分布关系也是海洋平台、海洋浮式设施等海洋结构物的重要设计参数(黄必桂等, 2017)。本文以散布图的形式(见图 6、图 7)刻画了波高和周期的联合分布规律。
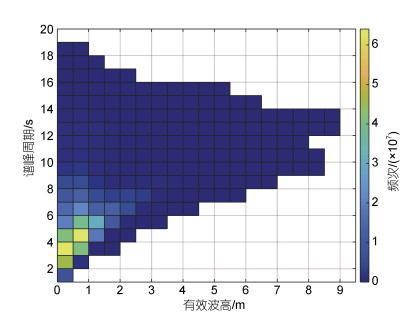 |
| 图 6 研究区域波高和波周期联合分布散点图 Fig. 6 Scatter map of joint distribution of wave height and wave period in the research area 注: 图像右侧颜色栏表示波浪发生频次 |
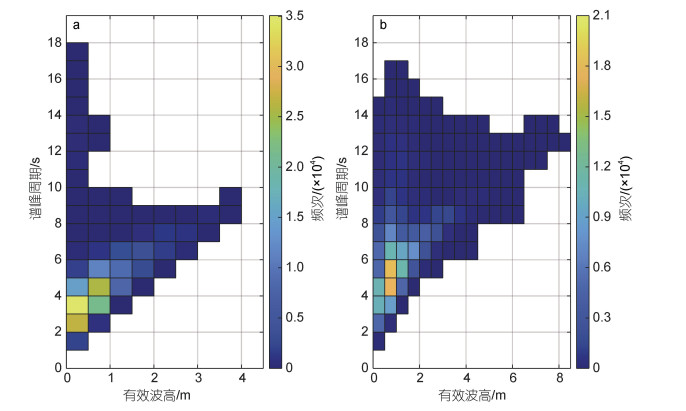 |
| 图 7 研究点A1 (a)、A2 (b)的波高和波周期联合分布散点图 Fig. 7 Scatter maps of joint distribution of wave height and wave period at the Sites A1 (a) and A2 (b) 注: 图像右侧颜色栏表示波浪发生频次 |
由图 6可知, 波高位于0.5~1.0 m并且波周期位于4.0~5.0 s的波浪在20年里是发生次数最多的, 随着波浪波高的增大以及波周期的增长, 各级波浪出现的次数逐渐变小, 0~0.5 m的波浪主要以大于2 s小于7 s周期的波居多, 0.5~2.0 m的波浪主要以大于4 s小于7 s周期的波居多, 大于2 m的波浪其波周期主要在6~16 s, 可见海浪波高较大时往往相对应的波周期也较长。从整体上而言, 20年里海浪以超过95%的概率发生在波高位于0~1.5 m, 波周期在0~7 s的范围内。
3.2 研究点波高和周期的联合分布特征以A1和A2为研究点, 对1999~2018这20年的黄渤海海域的波浪的波高和周期的联合分布特征进行了分析(见图 7)。A1点和A2点分别位于渤海内部莱州湾附近海域和黄海北部深海海域(见图 1), 代表了不同海区的波浪特征。
在A1点, 波浪的周期分布在0~18 s之间, 其分布在1~9 s的范围内逐渐递增, 周期大于9 s的情况开始急剧减少。其波高的分布在0~1.0 m的范围内最多, 波高大于1.0 m之后, 分布的情况逐渐减少。波高在0.5~4.0 m, 周期大于10 s的波浪几乎没有发生, 波高位于0~0.5 m并且波周期位于3.5~4.0 s的波浪在这20年里是发生次数最多的。在A2点, 波浪的周期分布在0~17 s之间, 其分布在1~13 s的范围内逐渐递增, 周期大于15 s的情况开始急剧减少。其波高的分布在0~2.0 m的范围内最多, 波高大于2.0 m之后, 分布的情况逐渐减少, 波高位于0.5~1.0 m并且波周期位于4.0~6.0 s的波浪在这20年里是发生次数最多的。相比于A1点, A2点波高周期分布比较均匀, 可能是由于A1点离岸近, 受水深和内陆影响导致, 而A2点处于深海区域, 水深大, 相对开阔无遮拦。
本文进一步对研究点(A1和A2) 20年的波高与周期的联合概率密度分布进行了研究, 为了比较方便, 将波高和周期无因次化, 分别以20年的平均波高Hm和平均周期Tm进行无因次化, 得到无因次波高Hs/Hm和无因次周期Tp/Tm, 统计得到研究点A1和A2波浪在每个区间的概率密度(表 1和表 2), 并绘制了概率密度分布图(图 8)。从图 8可以看出研究点A1和A2的波高和周期联合分布较为相似, 均呈现类似斜三角形分布。两个点最大概率密度均出现在Hs/Hm和Tp/Tm为1的附近, 并且大波高大周期的波浪与小波高小周期的波浪发生概率较小。
| Hs/Hm | Tp/Tm | ||||||
| 0.0~0.4 | 0.4~0.8 | 0.8~1.2 | 1.2~1.6 | 1.6~2.0 | 2.0~2.4 | > 2.4 | |
| 0.0~0.5 | 0.008 8 | 0.831 9 | 0.453 3 | 0.011 7 | 0.001 0 | 0.001 5 | 0.005 2 |
| 0.5~1.0 | — | 0.530 9 | 0.696 5 | 0.140 3 | 0.001 3 | 0.000 1 | 0.000 4 |
| 1.0~1.5 | — | 0.006 2 | 0.238 6 | 0.228 7 | 0.004 1 | 0.000 1 | — |
| 1.5~2.0 | — | — | 0.018 7 | 0.216 2 | 0.004 1 | 0.000 4 | — |
| 2.0~2.5 | — | — | — | 0.185 1 | 0.012 4 | 0.000 1 | — |
| 2.5~3.0 | — | — | — | 0.093 6 | 0.022 5 | — | — |
| 3.0~3.5 | — | — | — | 0.032 6 | 0.033 4 | — | — |
| > 3.5 | — | — | — | 0.005 6 | 0.057 9 | 0.004 1 | — |
| Hs/Hm | Tp/Tm | ||||||
| 0.0~0.4 | 0.4~0.8 | 0.8~1.2 | 1.2~1.6 | 1.6~2.0 | 2.0~2.4 | > 2.4 | |
| 0.0~0.5 | 0.026 0 | 0.660 2 | 0.358 8 | 0.097 9 | 0.017 3 | 0.009 9 | 0.000 2 |
| 0.5~1.0 | — | 0.618 9 | 0.991 6 | 0.272 4 | 0.048 0 | 0.027 6 | 0.002 0 |
| 1.0~1.5 | — | 0.099 5 | 0.667 5 | 0.128 6 | 0.045 5 | 0.021 7 | 0.001 0 |
| 1.5~2.0 | — | 0.000 5 | 0.325 1 | 0.095 0 | 0.018 5 | 0.010 8 | 0.000 4 |
| 2.0~2.5 | — | — | 0.093 6 | 0.125 0 | 0.005 9 | 0.002 5 | 0.000 1 |
| 2.5~3.0 | — | — | 0.011 0 | 0.107 8 | 0.001 4 | 0.000 7 | — |
| 3.0~3.5 | — | — | 0.000 7 | 0.057 3 | 0.000 7 | 0.000 2 | — |
| > 3.5 | — | — | 0.000 2 | 0.038 9 | 0.005 5 | 0.000 6 | — |
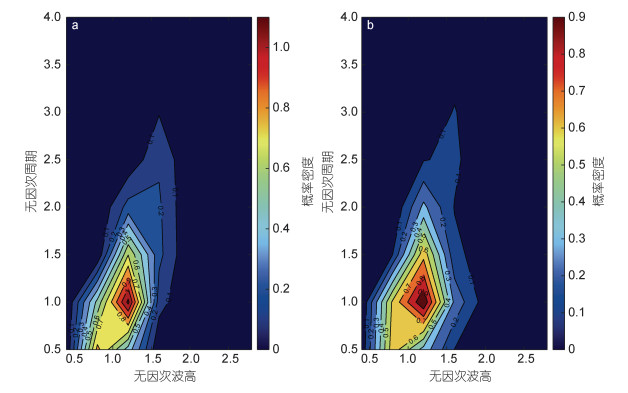 |
| 图 8 研究点A1 (a)、A2 (b)的波高和波周期联合分布 Fig. 8 Joint distribution of wave height and wave period at the Sites A1 (a) and A2 (b) |
海洋工程上在设计海上风机或者任何类型的海上结构时, 预测未来结构的长期极端响应或载荷是关键的一步。环境等值线法可独立于结构响应识别极限环境载荷, 通过在环境等值线上选取设计工况计算响应, 能够大幅减少仿真时间, 降低成本。
本文针对研究点(A1、A2) 20年的波浪后报数据, 构建了有效波高Hs和谱峰周期Tp的联合概率模型, 该模型可以表达为:
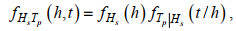 (1)
(1)式中, h和t分别表示有效波高和谱峰周期的数据。有效波高的边缘分布用Weibull分布来拟合, 其密度函数为:
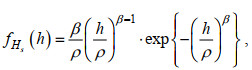 (2)
(2)式中, β和ρ分别表示Weibull分布的形状参数和尺度参数。条件密度函数使用对数正态分布, 其密度函数为:
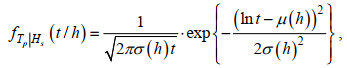 (3)
(3)式中, 参数μ(h)和σ(h)是在波高为Hs的情况下, 变量lnTp的期望和标准差。这两个参数可以通过属于一个范围内波高对应的周期来估计。为了推出观测范围以外的值, 用以下函数形式来拟合, 对应的参数估计如表 3所示。
 (4)
(4) (5)
(5)| 研究点 | 谱峰周期对数正态分布参数估计 | |||||
| a1 | a2 | a3 | b1 | b2 | b3 | |
| A1 | 0.823 (0.742, 0.904) |
0.545 (0.455, 0.635) |
0.638 (0.553, 0.723) |
–0.021 (–0.065, 0.023) |
0.431 (0.393, 0.469) |
0.488 (0.367, 0.609) |
| A2 | 1.008 (0.945, 1.071) |
0.639 (0.575, 0.703) |
0.407 (0.377, 0.437) |
0.063 (0.049, 0.077) |
0.469 (0.436, 0.502) |
0.622 (0.525, 0.719) |
式中, 系数ai和bi通过最小二乘法获取。
有效波高的边缘概率密度分布以及谱峰周期(Hs=0.6~1.1 m)的条件概率密度分布如图 9所示, 可以看出拟合公式非常符合实际数据的分布规律。基于有效波高和谱峰周期的联合概率密度函数, 采用IFORM法构造环境等值线。图 10展示了研究点A1和A2基于IFORM法的50年、100年和200年重现周期环境等值线, 为黄渤海区域海上结构物的可靠性设计提供了一定的参考。
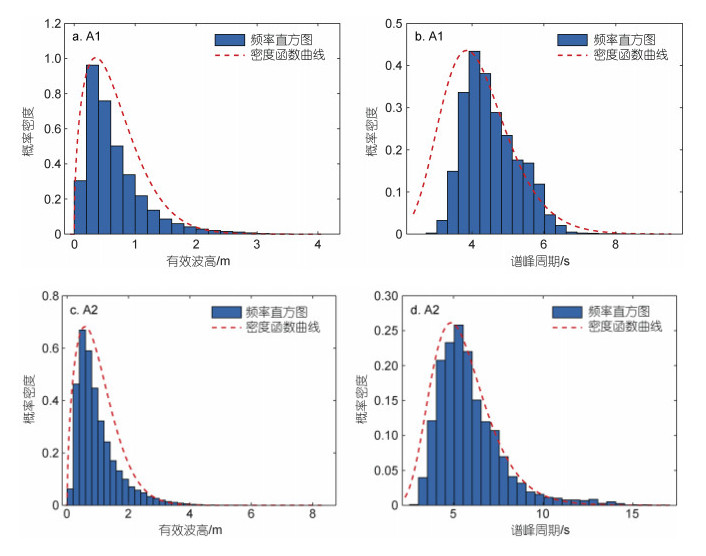 |
| 图 9 研究点A1、A2的有效波高和谱峰周期的概率密度分布 Fig. 9 Distributions in probability density of the significant wave height and spectral peak period at Sites A1 and A2 |
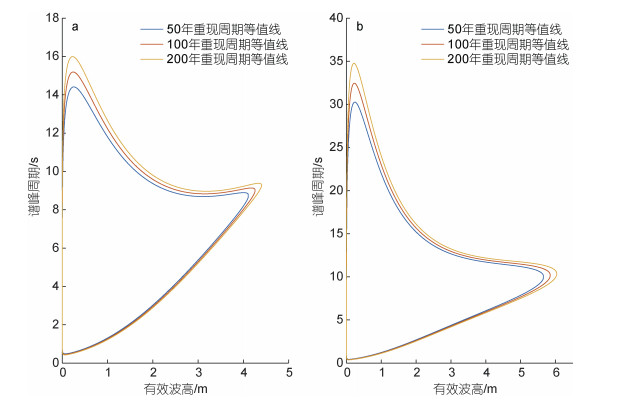 |
| 图 10 研究点A1 (a)、A2 (b)的环境等值线 Fig. 10 Environmental contours at Sites A1 (a) and A2 (b) |
本文采用SWAN模型模拟的波浪后报数据对中国黄渤海海域1999~2018年的波浪特征进行了统计分析。得到结论如下:
(1) 黄渤海海区波浪具有明显的季节性, 冬季有效波高平均值大于其他季节, 最大可达1.2 m, 主要因为冬季风暴是黄渤海的主导天气; 夏季波周期的平均值大于其他季节, 其最大可达到7.8 s。研究区域波浪具有明显的区域性特征, 受水深影响, 有效波高呈现出周边小, 中间大的特点; 波高和周期均呈现由南向北降低的趋势, 在黄海北部, 四个季节的有效波高平均值均大于1.0 m, 波周期的平均值均大于7 s; 在渤海海域, 四个季节的有效波高平均值均小于0.65 m, 四个季节的波周期平均值均不超过5 s。
(2) 研究区域20年波高最大值分布的区域性较为明显, 呈现由南向北逐渐减小的趋势, 在黄海北部最大可达到8.75 m, 在渤海区域, 均小于5.5 m。同样, 受水深影响, 波高的最大值分布呈现由深海向近岸逐渐减小的趋势。波周期最大值的分布较为均匀, 最大可达到19.5 s。
(3) 波高位于0.5~1.0 m并且波周期位于4.0~ 5.0 s的波浪是黄渤海海域20年里发生频次最多的。通过两个研究点(A1、A2)分析表明, 在黄渤海海域, 波高周期的联合分布基本呈类似斜三角形分布, 并且大波高大周期波浪的分布特征在渤海和黄海北部是有所差别的。
(4) 基于20年波浪后报数据构建的50年、100年和200年重现周期的环境等值线为黄渤海区域海上结构物的可靠性设计提供了一定的参考。
丁磊, 张鑫, 张晶, 2020. SWAN模型中不同破碎指标对波浪模拟的影响. 天津科技大学学报, 35(4): 36-40 |
王立国, 田香兰, 2012. 环黄渤海地区经济发展与合作的战略构想. 天津大学学报(社会科学版), 14(1): 19-24 DOI:10.3969/j.issn.1008-4339.2012.01.005 |
文先华, 武艺, 2016. 广西北海近岸海域波浪的分布特征. 水运工程, (7): 32-35 DOI:10.3969/j.issn.1002-4972.2016.07.007 |
乔守文, 孙嘉诚, 石洪源, 等, 2020. 基于ERA5的黄渤海附近海域波浪能资源时空特征分析. 海洋与湖沼, 51(6): 1350-1358 |
范琳琳, 2019. 基于WAVEWATCH-Ⅲ模式的中国南海波浪能资源的长期评估[D]. 天津: 天津大学: 33-40.
|
周昕伟, 徐福敏, 张继生, 2021. 几内亚湾海浪特性研究. 中国港湾建设, 41(9): 1-6 |
高晨晨, 周谷城, 王侃睿, 2019. 响水近岸海域波浪特性研究. 海洋学报, 41(5): 23-34 DOI:10.3969/j.issn.0253-4193.2019.05.003 |
唐军, 沈永明, 崔雷, 等, 2008. 随机波浪作用下近岸波流场的数值模拟. 力学学报, 40(4): 455-463 DOI:10.3321/j.issn:0459-1879.2008.04.004 |
姬厚德, 林毅辉, 蓝尹余, 等, 2021. SWAN模型在设计波浪要素计算中的应用研究. 应用海洋学学报, 40(3): 477-484 DOI:10.3969/J.ISSN.2095-4972.2021.03.012 |
黄必桂, 金嘉萌, 胡琴, 等, 2017. 基于实测资料的南海海浪波高和周期联合分布研究. 海洋工程装备与技术, 4(4): 187-192 |
谢欣, 陶爱峰, 张尧, 等, 2019. 基于波高和周期双指标的福建海域海浪危险性分析. 海洋通报, 38(2): 167-172 |
雷鹏, 张建侨, 2019. SWAN模型在硇洲渔港波浪要素推算中的应用. 河北渔业, (12): 12-15 |
潘冬冬, 周川, 王俊, 等, 2020. 粤东近岸深水区周年波浪特征分析. 南方能源建设, 7(4): 34-40 |
GAO H J, LIANG B C, SHAO Z X, 2021. A global climate analysis of wave parameters with a focus on wave period from 1979 to 2018. Applied Ocean Research, 111: 102652 |
SHAO Z X, LIANG B C, GAO H J, 2020. Extracting independent and identically distributed samples from time series significant wave heights in the Yellow Sea. Coastal Engineering, 158: 103693 |
SHI J, ZHENG J H, ZHANG C, et al, 2019. A 39-year high resolution wave hindcast for the Chinese coast: Model validation and wave climate analysis. Ocean Engineering, 183: 224-235 |
 2022, Vol. 53
2022, Vol. 53


