
中国海洋湖沼学会主办。
文章信息
- 尤再进. 2022.
- YOU Zai-Jin. 2022.
- 海洋重现期波高统一化计算方法
- UNIFIED APPROACH FOR ESTIMATION OF RETURN OCEAN WAVE HEIGHT
- 海洋与湖沼, 53(4): 1015-1025
- Oceanologia et Limnologia Sinica, 53(4): 1015-1025.
- http://dx.doi.org/10.11693/hyhz20220300051
文章历史
-
收稿日期:2022-03-08
收修改稿日期:2022-04-05
海洋波浪重现期/设计波高是港口海岸和海洋工程设计中不可回避的一个重要设计参数, 尤其对深水海港、沿海核电站、海洋平台、海底油气管线等重大涉海工程设计具有巨大的经济价值和深远的社会效益(尤再进, 2016)。国际学者采纳的设计波高或重现期波高的计算方法可以归纳以下三种: (1) 年n个大波法(annual n-largest method, ANL; 曹兵等, 2006), 此方法是由年极值法(n=1)延伸而来(Sobey et al, 1995), 从时间序列的波浪数据中每年提出n个独立的大浪峰值(n≥1), 组成一个极值波高数据样本, 然后应用广义极值函数(generalized extreme value, GEV)推算多年一遇的重现期波高; (2) 阈值法(peaks-over-threshold method, POT; Hosking et al, 1987), 该方法是设置统一的波高阈值H0, 从时间序列波浪数据中提出大于H0的独立大浪峰值, 组成一个极值波高数据样本, 然后应用广义帕累托函数(generalized Pareto distribution, GPD)推算极值波高; (3) 个风暴法(storm-by-storm method, SAS; Goda, 1988), 是从时间序列的波浪数据中提取所有风暴波浪峰值, 组成一个风暴波浪峰值数据样本, 然后应用右偏分布的概率函数(如Weibull、Pearson-Ⅲ等)推算重现期波高。
但是, 这三种重现期波浪计算方法通常会导致不同的计算结果。首先, 这三种极值波浪数据分析方法(ANL, POT, SAS)将会导致显著差异样本的重现期波高数据。Sartini等(2015)采用ANL和POT两种方法来计算百年一遇的极值波高, 发现这两种广义分布函数的计算结果差别很大。POT方法的难点是如何确定一个合适的波高阈值H0 (Liang et al, 2019)。You (2012)探讨了如何正确地选择极值波高阈值, 认为SAS是POT的一种特殊情况, 当POT的阈值等于SAS的当地最小台风/风暴波浪峰值时, 这两种方法就变成一种方法。ANL方法每年都提取n个独立和随机的大浪峰值, 而不能保证每年的波高阈值相同或者认为波高阈值是时间的变量, 而POT方法保持每年的波高阈值相同, 而每年获取的风暴波浪数不等, 或者认为POT方法每年提取的独立和随机大浪数是一个变量。所以, 这两种不同方法生成不同的极值波高数据样本, 导致重现期波高数据样本的不确定性。但是, 如果ANL方法每年选取的n个独立的最大波浪数据点是足够多(如n≥每年独立台风浪个数), 这两种方法能够生成几乎相同的重现期波高数据样本(You et al, 2015)。
其次, GEV和GPD是由不同的极值分析法而推导出的两种广义分布函数。理论上GEV只能由ANL方法生成的极值波高数据样本计算重现期波高, 同样GPD只能由POT方法生成的极值波浪样本来推算重现期波高。ANL或POT方法生成的极值波高数据样本和右偏分布的普通概率函数(如Weibull, Pearson-Ⅲ)也应用于重现期波高计算(尹宝树等, 2002)。Isaacson等(1981)指出, 没有一个极值分布函数是最佳的, 只有与具体数据比较以后, 才能够判断出哪个函数是最佳函数。
再者, 国内外学者们应用多种不同函数参数估算法计算极值函数参数, 如矩法(method of moment, MOM), 最小二乘(least-square method, LS), 极大似然(maximum likelihood method, ML), 概率权重矩(probability weighted moments, PWM)等参数估算方法, 其中MM, ML和LS是重现期波高计算中常用的三种主要参数估算法, 这些方法的物理含义比较清晰(陈子燊, 2011; You et al, 2015)。MM法应用比较简单, 从极值波高数据样本中分别估算出样本的均值、方差、偏度等特征参数。这就是概率论中n-阶矩的定义, 也就是波高变量的n次方对极值概率密度的积分。所以, MM方法通常适用于一些简单的两参数概率函数(如极值Ⅰ型分布, FT-Ⅰ), 而且极值波高数据样本量需要很大, 使得计算的极值波浪样本特征值(均值、方差、偏度)趋于稳定。ML方法适用于大多数极值函数, 但是在估算三参数或多参数函数的参数时(如Weibull, GEV, GPD), 其收敛速度比较慢, 甚至不收敛(Mazas et al, 2011)。You (2011)推广了LS方法, 高精度计算Weibull、GEV、GPD的三函数参数。基于澳大利亚新南威士州海岸采集的长期和高质量波浪数据, You (2012)定量讨论了ML和LS两种方法的关系, 研究发现LS方法是ML方法的一种特殊形式。很多学者认为, LS方法需要计算极值波高的经验频率分布, 而ML方法却不需要, 能够直接基于极值波浪数据样本确定极值函数参数。但是, 事实上所有极值波浪计算方法均需要重现期波高数据, 因为它们的计算结果需要与重现期波高数据进行比较。现有的经验频率计算公式大多是从序列函数推导出来的, 表达形式随着函数不同而改变, 导致生成不同的重现期波高数据样本(Goda, 1988)。基于波浪重现期的定义, You等(2015)推导出唯一的极值波浪经验频率的表达式, 消除重现期波高数据样本的不确定性。
最后, 国内外学者建立了不同的评估标准, 选择最佳候选极值函数推算重现期波高。现今应用最多的评估标准是均方误差(mean squared error, MSE): MSE=Σ(观测的重现期波高–计算的重现期波高)2/n, 其中, n是重现期波高数据样本量。但是, 也有少部分学者采用观测和计算的极值波高经验频率分布的均方误差MSE作为选择最佳极值函数的评估标准(Liu et al, 2021), 而极值波浪经验频率分布不是直接观测的极值波浪数据, 而且计算方法也具有不确定性。You等(2015)采用延伸的LS函数参数估算法, 建立了最佳候选极值函数评估标准, 其方法收敛快且精度高。
该论文重点研究重现期波高计算的统一化方法, 分析重现期波高计算中存在影响计算结果的不确定因素, 提出减少这些不确定因素的新方法, 建立一种误差小、应用方便、方法统一的重现期波高计算方法。
1 重现期波高计算控制方程给定一个三参数极值分布函数的一般表达式Q=f[(H−B)/A, α], 其中Q是大于或等于一个极值波高H的超越概率、B是位置参数、A是尺度参数、α是形状参数, 极值波高HQ可以从该极值分布函数中计算为
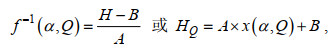 (1)
(1)其中, f−1(α, Q)是极值分布函数的反函数, x是函数变量。虽然方程(1)时常也应用于极值波高计算的控制方程, 但是重现期T常用于港口海岸和海洋工程的设计时间长度, 与超越概率Q的关系(You, 2012)为
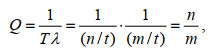 (2)
(2)其中, T=n/t是重现期值定义(CEM, 2002), n是t年观测波浪资料中共有的极值波高数据大于或等于重现期波高HT, m是t年观测波浪资料的极值波浪总数, λ=m/t是t年极值波浪的年均个数。将方程(2)代入方程(1), 重现期波高计算控制方程推导为
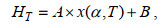 (3)
(3)其中, HT是T年一遇的重现期波高, x(α, T)是函数变量。方程(3)是重现期波高计算的控制方程, 仅是重现期T的函数。
控制方程(3)中的函数参数(A, B, α)能够通过线性回归重现期波高数据(x, HT)来确定。由于函数变量x是形状参数α的隐性函数, 函数参数(A, B)随着α的变化而变化。只有当α值满足和方差SSE最小要求时,
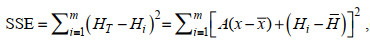 (4)
(4)函数参数(A, B)才能够使得SSE值最小, 其中SSE= MSE×m, HT是方程(3)计算的重现期波高, Hi是重现期波浪数据样本中的第i个观测波高, H是m个重现期波高的平均值, x是函数变量, x是极值函数变量的平均值, m是极值波浪数据点的总数。在方程(4)的两边, 对函数形状参数α求导:
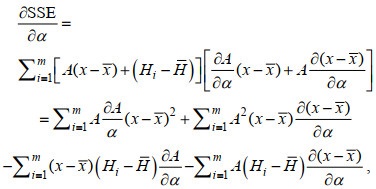 (5)
(5)其中函数参数A是方程(3)中的斜率, 且当SSE最小且∂SSE/∂A=0时, 可由方程(6)计算
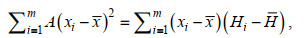 (6)
(6)并将其代入方程(5), 其第一项和第三项相加等于零, 方程(5)最后简化为
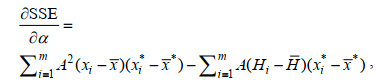 (7)
(7)其中xi*=∂xi/∂α和x*=∂xi/∂α当SSE最小时, 并令∂SSE/∂A=0, 形状参数α由方程(7)解得
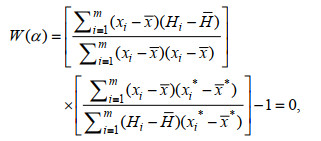 (8)
(8)方程(8)是函数形状参数α计算的控制方程, 乘号的前项是方程(6)的参数A或斜率, 乘号的后项相当于函数参数A的倒数(1/A)。Newton-Raphson迭代法可以应用于方程(8)的求解, 迭代求解函数形状参数α。虽然方程(8)与曹兵等(2006, 2007)和You等(2006)推导结果相同, 但是本文在推导过程中有显著差异, 尤其在方程(8)的推导过程中没有给出已知极值函数的具体表达式, 该方法适用于具有极值函数普通表达式Q=f[(H–B)/A, α]的显函数形状参数估算。
2 极值波高数据分析的逐个风暴法重现期波高数据(T, HT)是估算方程(3)函数参数(α, A, B)的基础数据, 是由极值波高数据(Q, H)并通过方程(2)转换而成, 这两组数据(Q, H)和(T, HT)其实是等同的。在现有的三种常用极值波高数据分析方法中, 逐个风暴法(图 1)是从长期时间序列的波高数据中逐个提取风暴/台风过程中的风暴波高峰值, 一个风暴过程仅提供一个风暴波高峰值的数据点, 提取的所有风暴波高峰值数据组成了独立和随机的极值波高数据样本。图 1中的时间序列波高数据来源于澳大利亚新南威士州的悉尼波浪骑士站(You et al, 2008), 每个风暴过程中的风暴有效波高峰值均大于风暴波高阈值3 m。逐个风暴法与波高阈值法存在一些明显区别, 尤其逐个风暴法中的风暴阈值是唯一的, 可由大气压场确定风暴刚刚开始的初时海况(You, 2012), 而POT阈值法中的波高阈值至今缺乏取值的统一标准, 人为影响因素比较大。但是, 这两种方法也是相关的, 逐个风暴法可以看作是POT阈值法的一种特殊形式: 当逐个风暴法中的风暴波高阈值等于阈值法中的波高阈值时, 这两种方法是等同的。
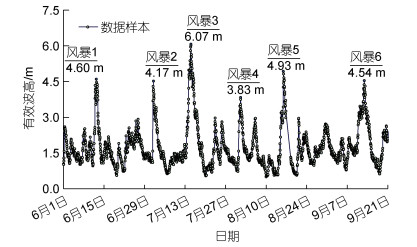 |
| 图 1 逐个风暴法应用于提取风暴过程中的波高峰值生成极值波高数据样本 Fig. 1 Extreme wave height dataset analyzed with the storm-by-storm analysis method |
本研究采用的重现期波高数据来源于澳大利亚新南威士州悉尼观测站的深水波浪数据(You et al, 2008)。该站的平均水深约80 m, 波浪数据从1976年开始采集, 一直持续至今。1986年前, 波浪数据纪录在图表纸上, 波峰值从图纸上测量。从1986起, 采用波浪骑士每0.5 s自动测量一个波高数据, 连续观测34 min, 每小时重复一次, 数据采集的成功率大于95%。基于悉尼站采集的25 a波浪数据(1987~2011年), 图 2给出了逐个风暴法分析的风暴波高峰值数据, 其中小圆圈数据点代表每个风暴过程中的最大有效波高, 方框中的数字代表年最大有效波高(年极值法), 大圆圈中的数字代表年风暴发生数次。该论文采用的悉尼站极值波高数据样本是由图 2中的从大到小排列的所有风暴波高峰值数据组成, 并应用方程(2)将极值波高数据(Q, H)转化成重现期波高数据(T, HT)。
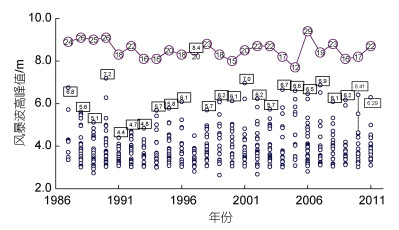 |
| 图 2 逐个风暴法分析获取的澳大利亚悉尼波浪观测站的极值波高数据 Fig. 2 Extreme wave height data analyzed by the storm-by-storm analysis method from Sydney waverider buoy on the NSW coast of Australia 注: 蓝色小圆圈数据点代表每个风暴波高峰值, 黑色方框中的数字代表年最大波高, 紫色大圆圈中的数字代表年风暴发生数次 |
重现期波高计算的候选极值函数众多, 大体可以归纳为3大类: 广义极值分布函数GEV、广义帕累托分布函数GPD、普通概率函数(如Weibull、Pearson-Ⅲ等), 它们的共性是右偏分布的长尾巴函数, 不同点是GEV应用于年n大波法的极值波高数据, GPD针对大于某个波高阈值的极值波高数据, 普通概率函数仅要求随机和独立的极值波高数据。因为GEV和GPD可以简化为等同的普通概率函数(You et al, 2015), 所以三类候选极值分布函数可以统一归类为右偏分布的普通概率函数。
3.1 广义极值函数如果暂先不考虑广义分布函数GEV推导的假设条件, GEV的复杂数学表达式可以直接简化为等同的指数函数表达式:
 (9)
(9)其中, A=σβ, B=(μ−σβ)和α=−σ。当α=±∞, α < 0和α > 0, 简化的GEV也分别称为FT-Ⅰ, FT-Ⅱ和FT-Ⅲ函数, 是否适用于重现期波高计算将通过均方差MSE收敛性得以判断。
在方程(3)中, 给定的不同函数参数α, 其他两个函数参数(A, B)由最小二乘法唯一确定。基于悉尼站的重现期波高数据, 图 3分别给出了方程(4)计算的均方误差MSE(α)和重现期波高H100随简化的FT-Ⅱ和FT-Ⅲ形状参数变化的分布规律。由图 3可见, FT-Ⅱ无最大值, 最小值收敛于FT-Ⅰ; FT-Ⅱ计算的MSE(α)存在最小值, 且当α > 100时逐渐收敛于FT-Ⅰ计算的MSE(α); FT-Ⅲ无最小值, 最大值收敛于FT-Ⅰ; 计算的MSE(α < 100)不存在最小值, 只有当α > 100时逐渐收敛于FT-Ⅰ计算的MSE(α)。所以, GEV的三种极值分布函数只有FT-Ⅱ适用于重现期波高计算的候选函数, 三参数的FT-Ⅱ包括二参数的FT-Ⅰ函数。
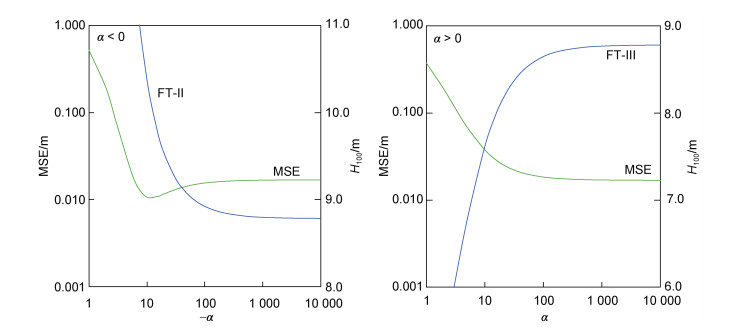 |
| 图 3 简化的广义极值分布函数(generalized extreme value, GEV)计算的均方误差MSE和重现期波高H100随简化的FT-Ⅱ和FT-Ⅲ形状参数α变化的分布规律 Fig. 3 Variations of mean-squared error MSE and 100-year return wave height H100 with shape parameter α calculated by the simplified GEV |
当FT-Ⅱ应用于重现期波高计算时, Newton-Raphson迭代法可以应用于计算方程(8)中的函数形状参数α, 其中xi*和x*分别计算为
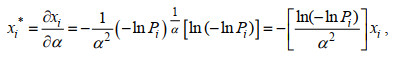 (10)
(10)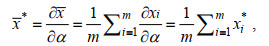 (11)
(11)其中, 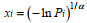
简化广义极值函数GEV有两个主要目的, 一是将复杂GEV表达式等同地简化为指数函数表达式, 并归类于普通的概率函数类; 二是能够极大简化方程(10)~(11)的函数变量求导, 应用方程(8)精确计算函数形状参数。
3.2 广义帕累托函数参考广义极值分布GEV的简化目的和方法, 广义帕累托分布GPD的复杂数学表达式也可以改写成简单的幂函数表达式:
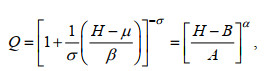 (12)
(12)式中, 简化后的GDP函数参数确定为A=σβ, B=(μ−σβ)和α=−σ。当α=±∞, α < 0和α > 0, 简化后的广义帕累托分布GPD也分别叫作GPD-Ⅰ, GPD-Ⅱ和GPD-Ⅲ, 它们是否是最佳候选极值函数可以通过均方差MSE收敛性得以判断。
基于悉尼站的同样重现期波浪数据, 图 4分别给出了均方误差MSE随GPD-Ⅱ和GPD-Ⅲ形状参数变化的分布关系, 以及百年一遇的重现期波高H100与形状参数α的变化规律。由该图可见, GPD-Ⅱ无最大值, 最小值收敛于GPD-Ⅰ或指数函数Q=exp[(H−B)/A], 计算的MSE(α)分布不存在最小值, 而GPD-Ⅲ无最小值, 最大值收敛于GPD-Ⅰ, 计算的MSE(α)分布存在最小值。所以, GPD的三种函数只有GPD-Ⅲ适用于重现期波高计算。
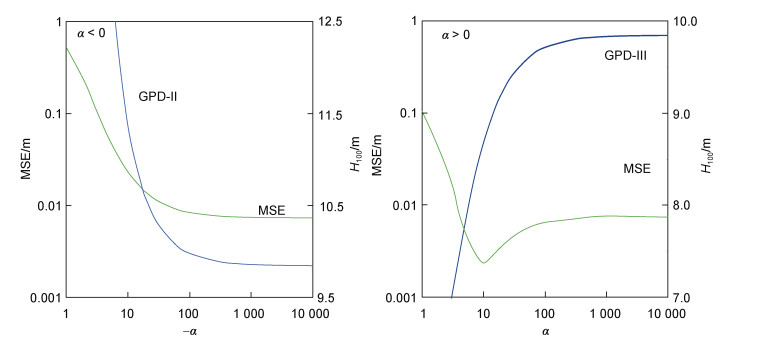 |
| 图 4 简化的广义帕累托函数(generalized pareto distribution, GPD)计算的均方误差MSE和重现期波高H100随函数形状参数α变化的分布规律 Fig. 4 Variations of mean-squared error MSE and 100-year return wave height H100 with shape parameter α calculated by the simplified GPD |
当GPD-Ⅲ应用于重现期波高计算时, Newton-Raphson迭代法用于计算方程(8)的函数形状参数α, 其中xi*计算为
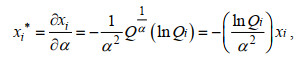 (13)
(13)x*由方程(11)计算, 其中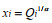
几种常采用的右偏分布概率函数(如Weibull和Pearson-Ⅲ)也应用于重现期波高计算。虽然简化后的GEV方程(9)的FT-Ⅲ(α > 0)与Weibull函数相似, 但不适用于重现期波高的计算(图 3), 且与Weibull(α > 0)分布函数完全不同
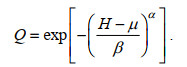 (14)
(14)基于相同的澳洲悉尼站重现期波浪数据, 图 5分别给出了均方误差MSE随Weibull和Pearson-Ⅲ形状参数变化的分布关系, 以及百年一遇的重现期波高H100与形状参数α的变化规律。由图 5可以看出, Weibull和Pearson-Ⅲ函数计算的MSE(α)均存在最小值, 但Weibull计算的MSE(α)要比Pearson-Ⅲ收敛要快。
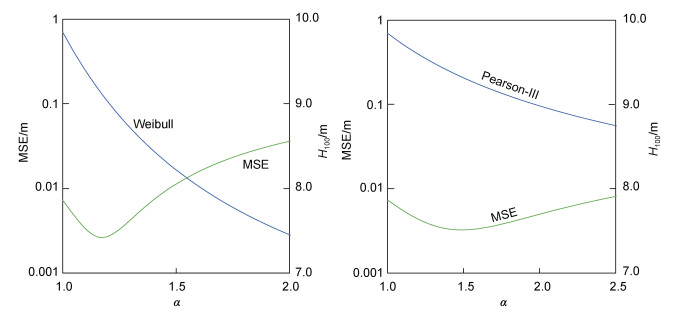 |
| 图 5 威尔布(Weibull)和皮尔逊3型(Pearson-Ⅲ)函数计算的均方误差MSE和重现期波高H100随函数形状参数α变化的分布规律 Fig. 5 Variations of mean-squared error MSE and 100-year return wave height H100 with shape parameter α calculated by Weibull and Pearson-Ⅲ |
类似于GEV和GPD形状参数的计算方法, Newton-Raphson迭代法也用于计算方程(8)的Weibull函数形状参数α, 但方程(11)和(12)中用于计算xi*和x*的累积概率P由超越概率Q代替, 函数变量为x=(−lnQ)1/α。因为Pearson-Ⅲ函数是非显性函数, 函数变量的导数比较复杂, 所以其函数形状参数α不能由方程(8)计算, 只能通过试算方法确定α, 使得方程(4)的SSE值最小(You, 2012)。
4 候选极值函数的最佳拟合标准 4.1 最佳拟合度评估法候选极值函数与重现期波高数据(T, HT)的拟合程度可由方程(4)计算的均方误差MSE或者和方差SSE值来评价。当MSE(α)最小或方程(8)W(α)=0, 候选极值函数与重现期波高数据的拟合程度达到最佳。基于悉尼波浪站的重现期波高数据, 两种简化的广义极值函数FT-Ⅱ方程(9)和GPD-Ⅲ方程(12)与重现期波高数据(x, HT)的线性拟合度见图 6, 其中x是极值函数变量, 函数形状参数α由方程(8)计算, 方程(1)中的函数尺度和位置参数(A, B)由最小二乘法确定。
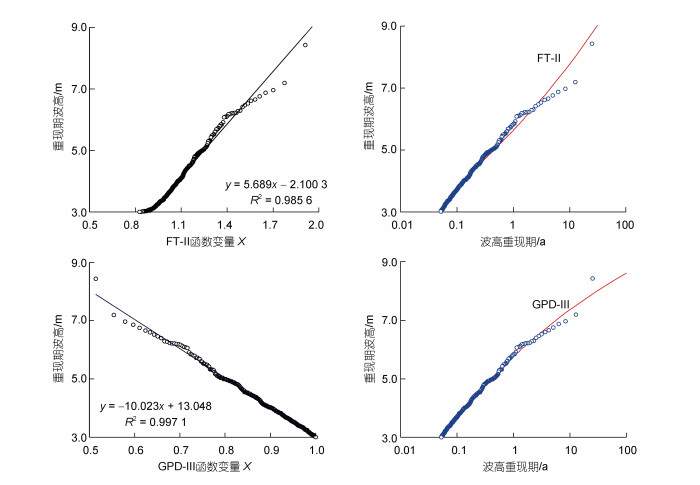 |
| 图 6 极值函数形状参数估算法方程(8)应用于简化的GEV-Ⅱ和GPD-Ⅲ参数估算和澳洲悉尼波浪站的重现期波高推算 Fig. 6 The shape parameters of simplified GEV-Ⅱ and GPD-Ⅲ are estimated by Eq.(8) and used to calculate return wave heights with different return periods at Sydney waverider buoy location on the NSW coast of Australia 注: 图中表达式为拟合直线, R为相关系数, 图 7同 |
图 6中的两种重现期波高数据(x, HT)和(T, HT)是等同的, 并具有相同的分布形态。这是因为当形状参数α确定后, x只是重现期T的唯一函数。当函数参数确定后, 重现期T是方程(1)中的重现期波高计算的唯一函数变量, 给定重现期T的波高HT能够从方程(1)获解。图 6也给出了计算的和观测的重现期波高的定量比较, FT-Ⅱ计算的重现期波高曲线具有上凸特点, 计算的重现期波高随T增加而较快增加, 而且计算红线均高于重现期大于4 a的波高, 高估了重现期波高。相比较而言, GPD-Ⅲ的重现期波高曲线具有上凹特点, 计算随T增加而较缓慢增加, 函数与数据的拟合度R2要比FT-Ⅱ的高。
图 7给出了Weibull和Pearson-Ⅲ概率函数与重现期波高数据(x, HT)的拟合度, 其中形状参数α先由方程(8)计算, 函数尺度和位置参数(A, B)再由最小二乘法计算。这两种概率函数与重现期波高的拟合度比较接近, 线性拟合系数R2几乎相等。图 7也给出了计算的重现期波高与重现期波高数据的定量比较, 计算的重现期波高曲线均具有上凹特点, Pearson-Ⅲ计算的重现期波高稍微比Weibull计算的大些。这可能是因为Weibull函数形状参数α是由方程(8)精确计算的, 而Pearson-Ⅲ的表达式是一个半隐性式, 函数形状参数只能通过试算方法来确定, 计算精度比较低。再者, 由图 5可见, 当MSE(α)靠近其最小值时, MSE(α)随形状参数α变化缓慢, 收敛性较差, 而Weibull计算的MSE(α)收敛性要比Pearson-Ⅲ的好些。
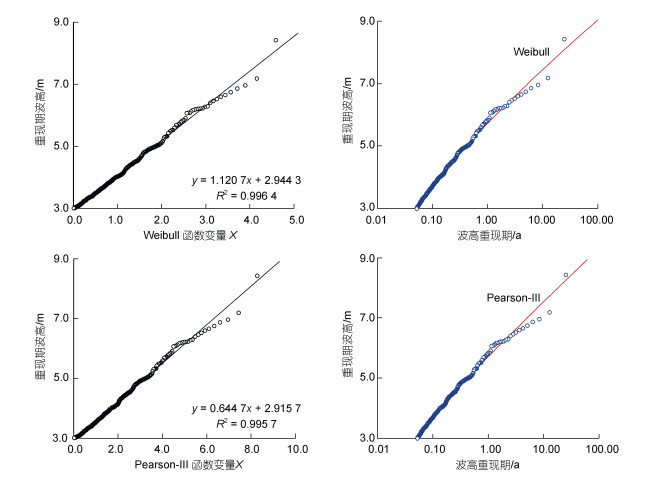 |
| 图 7 极值函数形状参数估算法方程(8)应用于概率函数Weibull和Pearson-Ⅲ参数估算和澳洲悉尼波浪站的重现期波高推算 Fig. 7 The shape parameters of Weibull and Pearson-Ⅲ are estimated by Eq.(8) and used to calculate return wave heights with different return periods at Sydney waverider buoy location on the NSW coast of Australia |
基于重现期波高计算控制方程(1)的推导假设条件, 仅当MSE(α)值最小时, 候选极值函数与重现期数据的拟合度才能达到最佳。但是, 应用于计算MSE(α)的重现期波高数据量m可能影响MSE(α)的收敛性以及该计算方法的适用性。同样基于悉尼站的重现期波高样本数据量, 不同样本的重现期波高数据(H1 > H2 > H3, …., > Hk)从悉尼站的重现期波高数据中(m=485)提取前k个重现期波高数据组成, 共计生产20个不同样本的重现期波高数据(k=25, 50, 75, 100, …., 450, 475)。其实, 这里的极值波高数据样本量是由波高阈值的取值大小决定的。
图 8给出了FT-Ⅱ计算的MSE(α)收敛性以及重现期波高H100随重现期波高数据量m增加的变化规律。由该图可以发现, MSE(α)均存在最小值, 但是当m < 150时, 其最小值位置和收敛值随m增大而分别向右方移动并明显减小, MSE最小值对应的重现期波高H100随着m增加而显著减小; 当m≥150时, MSE(α)最小值位置和收敛值随m增大而趋近稳定, 对应MSE最小值的重现期波高H100随着m增大而变化不显著。综上所述, 随着重现期波高数据m增加, FT-Ⅱ计算的MSE(α)始终存在最小值, 但仅当m≥150时, 计算的重现期波高H100才趋近稳定。这就要求采集的波高数据的时间长度(M年)应该足够长或者数据点足够多, 满足生成的极值波高数据量大于150。
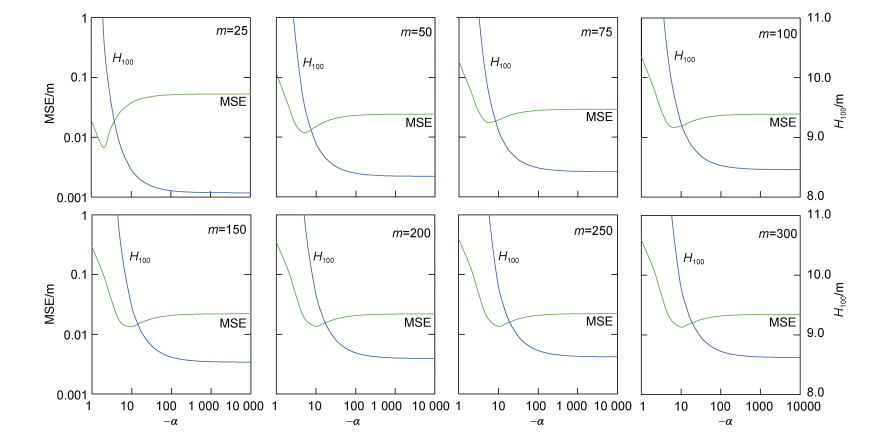 |
| 图 8 GEV-Ⅱ函数计算的MSE(α)收敛性和重现期波高H100随重现期波高数据样本量m的变化规律 Fig. 8 The variations of mean-squared error MSE (α) and 100-year return wave height, which are calculated by GEV-Ⅱ, with the sample size of extreme wave height data |
同样, 图 9也给出了GPD-Ⅲ计算的MSE(α) 收敛性以及重现期波高H100随数据量m增加的变化规律。由图可见, 当m < 50 (相当于年均采集两个极值波高数据点), MSE(α)不存在最小值, 但当α > 100时, MSE(α)开始收敛, 三参数的GPD-Ⅲ简化为两参数的指数函数Q=exp[(H−B)/A]; 当m≥200, MSE(α)存在最小值, 其最小值位置和收敛值随m增大而趋近稳定, MSE最小值对应的重现期波高H100随着m增大而没有显著变化, GPD-Ⅲ计算的重现期波高H100随m增大而趋向稳定。所以, 当重现期波高数据量m比较小时, GPD-Ⅲ概率函数不适用于计算重现期波高, 仅当m≥200重现期波高计算才趋近稳定。
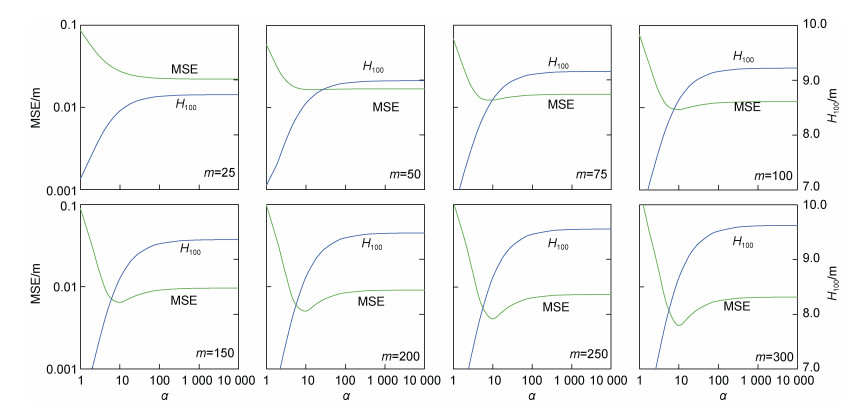 |
| 图 9 GPD-Ⅲ计算的MSE(α)收敛性与重现期波高H100数据随样本大小m的变化规律 Fig. 9 The variations of mean-squared error MSE(α) and 100-year return wave height, which are calculated by GPD-Ⅲ, with the sample size of extreme wave height data |
再次, 图 10给出了Weibull计算的MSE(α)收敛性以及重现期波高H100随数据量m增加的变化规律。由图可见, 当m < 25时(相当于年均有一个极值波高数据点), 在形状参数的适用范围内(1 < α < 2), MSE(α)不满足方程(1)的推导条件∂MSE/∂α=0, 导致Weibull函数不适用于重现期波高计算; 当50≤m < 200时, MSE(α)均存在最小值且∂MSE/∂α=0, 但MSE收敛于最小值的速度很慢, 而靠近MSE最小值附近的重现期波高变化较大, 这意味着由Weibull函数计算的重现期波高受其形状参数α计算精度的影响比较显著; 仅当m≥200, MSE(α)存在最小值, 其最小值位置和收敛值随m增大而趋近稳定, MSE最小值对应的重现期波高H100随着m增大而没有显著变化, Weibull计算的重现期波高H100随m增大而趋向稳定。综上所述, 当重现期波高数据量m比较小时, Weibull概率函数不适用于重现期波高计算, 但当数据量足够大时(m≥200), 计算的重现期波高H100才趋近稳定, 重现期波高计算受形状参数计算精度的影响较显著。
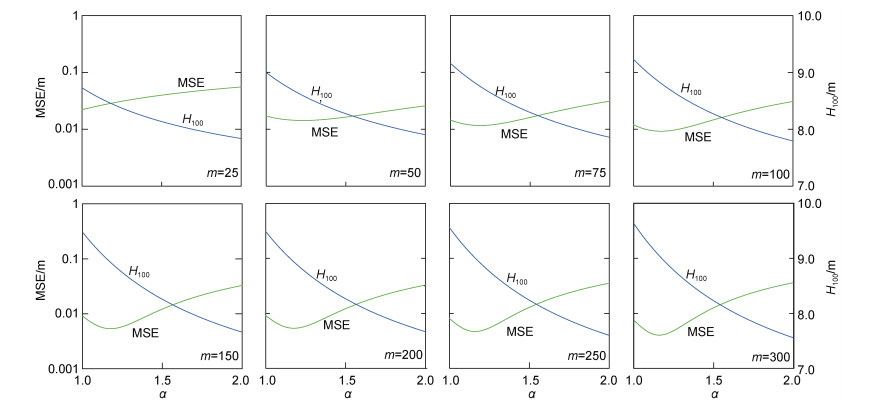 |
| 图 10 Weibull函数计算的MSE(α)收敛性与重现期波高H100数据随样本大小m的变化规律 Fig. 10 The variations of mean-squared error MSE(α) and 100-year return wave height, which are calculated by GPD-Ⅲ, with the sample size of extreme wave height data |
最后, 图 11给出了Pearson-Ⅲ和Gumbel(FT-Ⅰ)计算的重现期波高与年极值法分析的重现期波高数据的定量比较, 这两函数是《港口与航道水文规范》(JTS145-2015)推荐的极值波高数据分析法和候选极值分布函数。由图 7和图 11可见, 逐个风暴法(SBS)构建的重现期波高数据样本(m=285)远远大于由年极值法生成的极值波高数样本量(m=25); Pearson-Ⅲ基于年极值法计算的百年一遇重现期波高(H100=9.19 m)大于基于SBS法计算的重现期波高H100=8.63 m, 两者误差约6.5%。再比较图 8和图 11可知, Gumbel基于年极值法计算的百年一遇重现期波高(H100=8.94 m)略大于基于SBS法计算的重现期波高H100=8.78 m, 两者计算方法相差1.8%, 但较小于Pearson-Ⅲ推算的H100=9.19 m, 其中当α→∞时, 图 8中FT-Ⅱ计算的重现期波高等于FT-Ⅰ计算的。
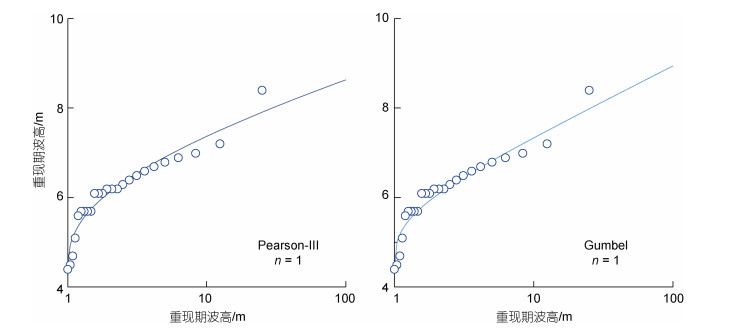 |
| 图 11 Pearson-Ⅲ和Gumbel (FT-Ⅰ)计算的重现期波高与年极大值法分析的重现期波高数据的比较 Fig. 11 Comparison of return wave heights with different return periods calculated by Pearson-Ⅲ and Gumbel (FT-Ⅰ) with the return wave height data analyzed by the annual maximum method 注: n表示年平均极值波高的数量 |
重现期波高是港口海岸及海洋工程设计中不可回避的一个重要设计参数, 但其计算方法至今缺乏统一性, 计算结果存在显著不确定性。该论文建立了一种误差小、应用方便、方法统一的重现期波高计算方法。本文研究发现: GPD-Ⅲ和Weibull是重现期波高计算的最佳候选推算函数, 新推导的它们形状参数计算公式较好提高重现期波高的计算精度, 极值波高数据的样本量和分析方法是影响重现期波高计算精度的2个重要因素。基于上述的研究发现, 我国《港口与航道水文规范》(JTS 145—2015)建议采用的年极值法和Pearson-Ⅲ极值分布函数有可能高估推算的重现期波高, 但需要中国沿海长期且高质量现场波浪数据进一步验证。逐个风暴的极值波高数据分析法与广义帕累托函数GPG-Ⅱ和Weibull建议应用于涉海工程的重现期波高计算。
尤再进, 2016. 中国海岸带淹没和侵蚀重大灾害及减灾策略. 中国科学院院刊, 31(10): 1190-1196 |
尹宝树, 何宜军, 侯一筠, 等, 2002. 推算波浪多年一遇波高的新方法. 海洋与湖沼, 33(1): 30-35 DOI:10.3321/j.issn:0029-814X.2002.01.005 |
陈子燊, 2011. 波高与风速联合概率分布研究. 海洋通报, 30(2): 158-163 DOI:10.3969/j.issn.1001-6392.2011.02.006 |
曹兵, 王义刚, YOU Z J, 2006. 三种设计波高计算方法比较. 海洋工程, 24(4): 75-80 DOI:10.3969/j.issn.1005-9865.2006.04.013 |
曹兵, 王义刚, YOU Z J, 2007. 设计波高分布函数比较. 海洋湖沼通报, (4): 1-9 DOI:10.3969/j.issn.1003-6482.2007.04.001 |
CEM, 2002. Hydrodynamic Analysis and Design Conditions[M]. U. S Army Corps of Engineers, Coastal and Hydraulics Laboratory.
|
GODA Y, 1988. On the methodology of selecting design wave height[C]//Proceedings of the 21st International Conference on Coastal Engineering. Costa del Sol-Malaga: ASCE: 899-913.
|
HOSKING J R M, WALLIS J R, 1987. Parameter and quantile estimation for the generalized Pareto distribution. Technometrics, 29(3): 339-349 DOI:10.1080/00401706.1987.10488243 |
ISAACSON M S Q, MACKENZIE N G, 1981. Long-term distributions of ocean waves: a review. Journal of the Waterway, Port, Coastal and Ocean Division, 107(2): 93-109 DOI:10.1061/JWPCDX.0000257 |
LIANG B C, SHAO Z X, LI H J, et al, 2019. An automated threshold selection method based on the characteristic of extrapolated significant wave heights. Coastal Engineering, 144: 22-32 DOI:10.1016/j.coastaleng.2018.12.001 |
LIU G L, CUI K, JIANG S, et al, 2021. A new empirical distribution for the design wave heights under the impact of typhoons. Applied Ocean Research, 111: 102679 DOI:10.1016/j.apor.2021.102679 |
MAZAS F, HAMM L, 2011. A multi-distribution approach to POT methods for determining extreme wave heights. Coastal Engineering, 58(5): 385-394 DOI:10.1016/j.coastaleng.2010.12.003 |
SARTINI L, MENTASCHI L, BESIO G, 2015. Comparing different extreme wave analysis models for wave climate assessment along the Italian coast. Coastal Engineering, 100: 37-47 DOI:10.1016/j.coastaleng.2015.03.006 |
SOBEY R J, ORLOFF L S, 1995. Triple annual maximum series in wave climate analyses. Coastal Engineering, 26(3/4): 135-151 |
YOU Z J, 2011. Extrapolation of historical coastal storm wave data with best-fit distribution function. Australian Journal of Civil Engineering, 9(1): 73-82 DOI:10.1080/14488353.2011.11463965 |
YOU Z J, 2012. Discussion of "a multi-distribution approach to POT methods for determining extreme wave heights" by Mazas and Hamm, [coastal engineering, 58:385-394]. Coastal Engineering, 61: 49-52 DOI:10.1016/j.coastaleng.2011.11.004 |
YOU Z J, LORD D, 2008. Influence of the El Niño-southern oscillation on NSW coastal storm severity. Journal of Coastal Research, 24(sp2): 203-207 |
YOU Z J, YIN B S, 2006. Estimation of extreme coastal wave heights from time series of wave data. China Ocean Engineering, 20(2): 225-241 |
YOU Z J, YIN B S, JI Z Z, et al, 2015. Minimisation of the uncertainty in estimation of extreme coastal wave heights. Journal of Coastal Research, 75(sp1): 1277-1281 |
 2022, Vol. 53
2022, Vol. 53

