中国海洋湖沼学会主办。
文章信息
- 何群, 高艳秋, 唐佑民, 张继才. 2022.
- HE Qun, GAO Yan-Qiu, TANG You-Min, ZHANG Ji-Cai. 2022.
- 一种新的模式倾向误差估计算法及其在ENSO模拟中的应用
- A NEW ALGORITHM OF ESTIMATION FOR MODEL TENDENCY ERRORS AND THE APPLICATION IN ENSO SIMULATION
- 海洋与湖沼, 53(5): 1067-1078
- Oceanologia et Limnologia Sinica, 53(5): 1067-1078.
- http://dx.doi.org/10.11693/hyhz20220100009
文章历史
-
收稿日期:2022-01-12
收修改稿日期:2022-03-10
2. 自然资源部第二海洋研究所卫星海洋环境动力学国家重点实验室 浙江杭州 310012;
3. 南方海洋科学与工程广东省实验室(珠海) 广东珠海 519082;
4. 河海大学海洋学院 江苏南京 210098
2. State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography, Ministry of Natural Resources, Hangzhou 310012, China;
3. Southern Marine Science and Engineering Guangdong Laboratory, Zhuhai 519082, China;
4. College of Oceanography, Hohai University, Nanjing 210098, China
厄尔尼诺-南方涛动(El Niño-Southern Oscillation, ENSO)是短期气候年际变化的最强信号之一(连涛等, 2017), 主要表现为热带太平洋海表面温度每隔2~7 a的大范围变暖或变冷, 其中暖事件称为厄尔尼诺(El Niño), 冷事件称为拉尼娜(La Niña)。ENSO影响着全球的温度和降水, 它的发生往往会在全球多地造成严重的自然灾害, 如El Niño期间澳大利亚、印度尼西亚等地的炎热干旱, 南美太平洋沿岸国家的暴雨洪涝, 以及我国的南涝北旱。而La Niña与El Niño作用相反, 当La Niña事件发生时, 南美洲地区旱情严重, 东南亚、澳大利亚等地区会出现暴雨, 甚至出现洪涝灾害(夏咏华, 2001; 王琳等, 2019)。因此, ENSO研究一直是大气海洋领域的热点和焦点。
近几十年里, ENSO的观测、模拟和预报研究取得了长足进展, 目前国际上已有20多个模式提供6~12个月的ENSO预报(https://iri.columbia.edu/our-expertise/climate/forecasts/enso/current/), 但它们普遍存在一定的预报误差, 特别是对历史上几次El Niño事件的错误预报严重制约了ENSO的实际预报技巧(穆穆等, 2017)。此外, 近些年来中部型El Niño事件频发(Yeh et al, 2009), 给模式的模拟和预报带来了新的挑战。因此, 如何减小模式误差, 提高模式对ENSO的模拟、预报能力, 是一项十分重要且前沿的工作。
影响ENSO预报技巧的因素主要分为初始误差和模式误差两种。与初始误差相关的研究十分丰富且成熟: 一方面, 可通过数据同化方法优化模式预报的初始条件(Chen et al, 1997, 1998), 另一方面, 可通过加强对重点区域的观测, 获取更有效的观测资料, 优化模式初始场(Mu et al, 2015; Hu et al, 2016)。除初始误差外, 越来越多的研究开始关注模式误差的影响(Qi et al, 2017), 且有研究表明, 对初始误差的改进仅能在提前几个月的预报中体现, 而对模式误差的改进能提高长期预报的技巧(Zheng et al, 2009)。
模式误差主要来源于物理内核不匹配、物理方案近似和参数误差三个方面(Wu et al, 2016)。鉴于改进前两个方面的难度, 许多学者通过改进参数误差来降低模式误差。然而, 针对模式参数的优化通常只能优化特定的参数。因此, Roads (1987)提出在状态趋势方程中添加一个常数项F, 称为恒定倾向误差, 用于表示多种来源模式误差的综合效应, 并利用观测信息估计恒定倾向误差。依据这一思想, Moore等(1999)在随机动力系统的框架下, 把倾向误差视为随机误差, 并利用随机最优理论来定量计算增长最快的随机误差, 即最优强迫向量。这种最优强迫向量能刻画ENSO预报的最大不确定性, 被广泛应用在集合预报中。但Barkmeijer等(2003)认为这种最优强迫向量的计算量巨大, 不适用于现实中的高维非线性数值模式。为了解决这一限制, 他们提出了线性强迫奇异向量(forcing singular vector, FSV)方法, 通过求解线性最优问题得到一个不随时间变化的倾向误差。在此基础上, Duan等(2013)将FSV方法进行扩展, 发展出非线性强迫奇异向量(non-linear forcing singular vector, NFSV)方法, 基于变分思想计算得到随时间和空间变化的最优倾向误差。他们(Duan et al, 2014)将NFSV方法应用于著名的Zebiak-Cane (ZC)模式, 对1980~2004年间三次典型的东部(Eastern-Pacific, EP)型El Niño事件和三次典型的中部(Central-Pacific, CP)型El Niño事件进行模拟, 结果表明, 使用NFSV方法校正的ZC模式, 不仅能够重现EP型El Niño事件, 并且很好地再现了三次CP型El Niño事件。基于此, Tao等(2019)进一步建立了NFSV型倾向误差预报模式, 将预报模式与中间型海洋—大气耦合模式(Intermediate Complex Model, ICM)耦合, 构建了ENSO的NFSV-ICM预报模式, 并对1997~2016年间的ENSO事件进行预报实验。与ICM模式相比, NFSV-ICM具有更高的预报技巧, 有效预报时效从6个月提高至12个月。
如果视每个模式格点的倾向误差是一个参数, 那么倾向误差估计实质等价于资料同化中的参数估计。因此, 除了变分方法外, 目前常用于资料同化的集合卡尔曼滤波器及其变种在理论上都可以应用于倾向误差估计(吴新荣, 2013)。此外, 与四维变分方法相比, 卡尔曼滤波器无需发展伴随模式, 计算较为简单, 同时考虑了预报误差的动力演变, 可以显式地提供预报的初始扰动(沈浙奇等, 2016)。基于此, 本研究拟发展一种基于集合卡尔曼滤波器的模式倾向误差估计算法, 通过同化海表面温度异常(sea surface temperature anomaly, SSTA)数据来计算模式倾向误差, 并考察其对ENSO模拟的影响。
本文分为三个部分。第一部分介绍了研究所用的模式、观测资料和模式倾向误差估计算法的具体内容。第二部分为模式倾向误差的估计及其在ENSO模拟中的应用。最后一部分是总结和讨论。
1 模式与方法 1.1 Zebiak-Cane模式ZC模式(Cane et al, 1985, 1986; Zebiak et al, 1987)是拉蒙特-多尔蒂地球观测站(Lamont-Doherty Earth Observatory, LDEO)的业务化预报模式, 显式地描写了Bjerknes-Wyrtki理论的物理本质(徐辉, 2006), 因成功预报出了1986~1987年的El Niño事件而著名, 被广泛地应用于ENSO研究(Chen et al, 1995, 2004, 2008; Gao et al, 2020)。
ZC模式由海洋斜压模式、海洋表层模式和大气模式耦合而成, 其中海洋斜压模式决定海洋对风强迫的响应, 海洋表层模式用于计算SSTA, 而大气模式用来模拟风对SSTA的响应(Perigaud et al, 1996; 岳彩军等, 2004)。海洋模式中, SSTA的发展方程(徐辉, 2006)为
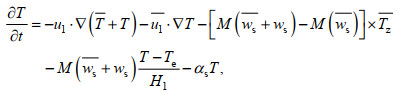 (1)
(1)式中, T为海表面温度距平; u1为表面流水平流速距平; T为月平均海表温度; u1为气候平均的水平流速; 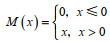
我们在ZC模式的SSTA订正方程中引入代表模式倾向误差项的参数F(i, j, t):
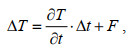 (2)
(2)式中, Δt为模式积分步长, 为10 d。
1.2 观测资料观测资料采用的是美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA) ERSST v5数据集内的月平均SSTA数据, 数据分辨率为2°×2°, 区域范围选取101.25°E~73.125°W, 29°S~29°N, 与ZC模式区域一致, 时间长度选取1950年1月至2020年12月, 共852个月。需要对选取的SSTA数据进行预处理: 为了与ZC模式网格分辨率一致, 将数据插值到5.625°×2.000°的网格分辨率, 然后使用100个符合均值为0, 方差为0.1 ℃ (Huang et al, 2016)的高斯分布的随机数对其进行扰动。
1.3 LETKF框架下的倾向误差估计算法当集合卡尔曼滤波器(ensemble Kalman filter, EnKF)同化技术被用于多维海气模式时, 使用有限的集合样本来估计背景误差协方差矩阵会经常导致伪相关问题(Tang et al, 2016), 而局地集合变换卡尔曼滤波器(local ensemble transform Kalman filter, LETKF)同化技术(Hunt et al, 2007)能克服远距离虚假相关这一缺点, 在海洋和气象领域有着广泛的应用。例如, Ruckstuhl等(2020)采用LETKF技术估计了COSMO-DE模式中的二维粗糙长度参数, 改进了模式对降水和云的预报。Gao等(2021)基于LETKF技术建立了ZC模式的同化系统, 对模式的关键参数进行估计, 发现参数估计降低了模式误差, 提高了模式对ENSO的预报效果。因此, 本文选取LETKF同化技术作为估计模式倾向误差参数的方法。
由于现实中没有参数的直接观测, 所以参数的估计是通过状态向量附加技术(state vector augmentation technique, SVAT)实现的, 具体来说, 就是把参数视作状态向量的一部分, 在进行参数估计时使用状态向量的观测算子(吴新荣, 2013)。计算步骤如下:
(1) 首先假定状态向量有N个集合成员xnb (n=1, 2, …, N), 集合平均为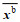
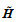
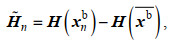 (3)
(3)其中, H表示将模式格点的变量投影到观测空间上的线性观测算子, 插值过程基于双线性插值方法。
(2) 计算卡尔曼增益矩阵
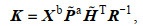 (4)
(4)式中, Xb是集合扰动矩阵, 其第n列元素为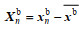
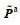
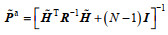
(3) 计算分析场的集合平均:
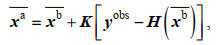 (5)
(5)其中, yobs代表状态向量的观测。
(4) 为了更新每个集合成员, LETKF还需计算分析集合扰动。通过一个变换矩阵, 可将背景场扰动Xb转换成分析场扰动Xa, 得到分析集合的扰动为
 (6)
(6)(5) 将分析集合扰动加到分析集合平均上, 可得更新的分析成员xa,
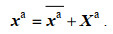 (7)
(7)基于以上计算步骤, 在给定待估参数F初始场的前提下, 可计算得到参数在每一步的分析值, 取集合均值为最终分析结果。如此, 得到倾向误差F在不同模式格点和时间点的估计值。
2 结果与分析 2.1 模式倾向误差的计算及分析 2.1.1 倾向误差估计初始场设计使用LETKF同化技术对参数进行估计时需要给出待估参数的初始值。由于参数F代表的是模式的倾向误差, 没有实际观测数据, 因此, 我们将ZC模式只进行状态估计(only state estimate, OSE)时同化输出的SSTA分析值与观测值的偏差(error)即模拟误差作为待估参数的初始场, 这种偏差一定程度上代表了模式误差, 并使用一组符合均值为0, 方差为0.1 ℃的高斯分布的随机数对其进行扰动, 生成100个数据集合, 作为参数F的初始集合。同样对初始时刻的SSTA进行扰动, 生成状态变量SSTA的初始集合。
图 1a展示了SSTA观测值和OSE实验分析值的Niño 3.4指数时间序列, 图 1b为观测值减去实验分析值所得的差值。可以看出, 运用LETKF同化技术得到的SSTA分析值和观测值具有很好的相关性, 如表 1所示, 相关系数高达0.97, 相比同化前0.86的相关系数有较大提高, 且平均绝对误差由同化前的0.32降低到了0.15, 这说明了LETKF同化技术的有效性。但从图 1b可见, 分析值和观测值之间仍存在一定的差异, 偏差多为负值, 表明模式常常高估于观测, 尤其是在冷事件的模拟上, 差值最大达到了0.8 ℃, 且冷事件模拟的偏差普遍高于暖事件的偏差。
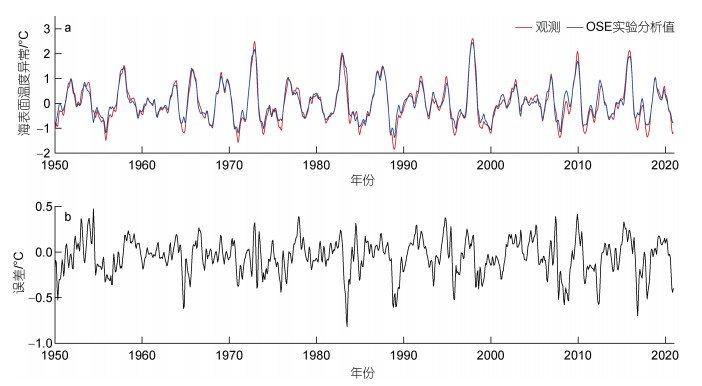 |
| 图 1 海表面温度异常(sea surface temperature anomaly, SSTA)观测值(红)与OSE实验分析值(蓝)的Niño 3.4指数时间序列(a)以及两者的差值(b) Fig. 1 The Niño 3.4 index time series of observed SSTA (red) and OSE SSTA (blue) (a) and the difference between them (b) 注: OSE: only state estimate, 仅进行状态估计实验 |
| 实验阶段 | 相关系数 | 平均绝对误差/℃ |
| 同化前 | 0.86 | 0.32 |
| 同化后 | 0.97 | 0.15 |
得到倾向误差估计所需的初始场之后, 使用LETKF同化技术对倾向误差进行估计。通常, 基于卡尔曼滤波器的同化实验是从一个初始时刻出发, 在模式的积分过程中将观测数据同化进模式, 对模拟结果进行校正, 以输出更为接近观测状态的分析值。同样, 在进行参数估计时, 也是从某一初始时刻起, 通过同化观测资料对参数进行调整。例如, 以1950年1月为起始月, 基于该月的初始场, 同化SSTA数据对模式倾向误差进行估计, 我们发现, 随着同化的进行, 参数分析值在经过一段时间(大约10 a)的调整后趋于稳定。为了进一步验证该结论, 基于1950年1月至2011年1月间共733个月的初始场, 计算对应的模式倾向误差。结果表明, 倾向误差估计值均经过约10 a的调整后趋于稳定, 且不同起始月份得到的稳定值不同。为了表述简洁, 图 2仅展示了1950年1月至1951年1月间不同起始月份对应的倾向误差估计值。因此, 我们可以认为, 模式倾向误差与起始月份所给定的参数初始场之间存在一定的相关关系。从式(5)和式(6)也可以看出, 参数的分析值会受到初始值的影响。我们将稳定后的估计值作为对应于不同起始月的模式倾向误差估计值, 并基于这些估计值展开分析。
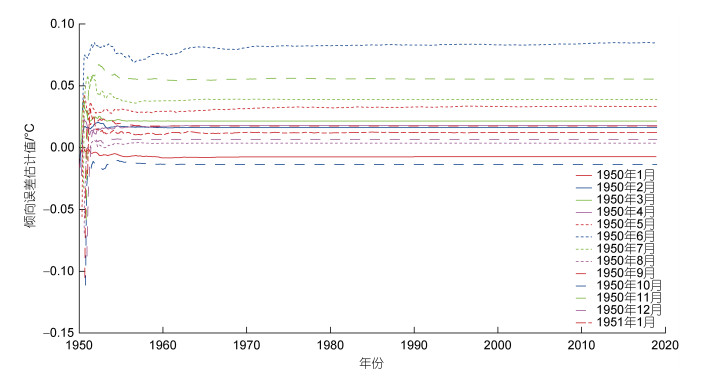 |
| 图 2 分别以不同起始月份为起点得出的模式倾向误差估计值在模式区域的平均 Fig. 2 The average estimates of model tendency error in model area obtained from different starting months 注: 图中所示起始月份为1950年1月至1951年1月 |
为了检验模式倾向误差估计实验中同化的有效性, 将同化得到的倾向误差估计值加入ZC模式, 重复OSE实验, 发现SSTA分析值和观测值的相关性较不含模式倾向误差项的OSE实验略有提高, 由0.970提高到了0.972, 且平均绝对误差进一步由0.15降低至0.13, 体现了LETKF同化技术在估计模式倾向误差上的有效作用。
2.1.3 倾向误差特征由于Niño3.4区域是表征ENSO特征的一个关键区域, 所以图 3展示了Niño 3.4区域平均的倾向误差估计值及其对应的误差(即观测值和OSE实验分析值的差值)。可以看到, 倾向误差估计值与误差相关较好, 两者的相关系数为0.71, 表明倾向误差估计值可以在一定程度上代表模式误差。
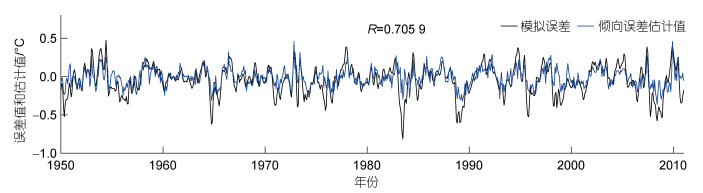 |
| 图 3 误差(黑)和模式倾向误差估计值(蓝)在Niño 3.4区域的平均 Fig. 3 The average of the error (black) and the model tendency error estimates (blue) in the Niño 3.4 area 注: R表示相关系数 |
为了进一步比较两者在赤道地区的演变特征, 图 4展示了误差(a)和倾向误差估计值(b)在5°S~5°N区域平均的时间—经度剖面图。可以看到, 在时间和空间上, 两场都有较好的对应关系。当误差场中出现一个正(负)差值时, 相应地, 在倾向误差场也会出现正(负)值, 两场的相关系数达到了0.63。
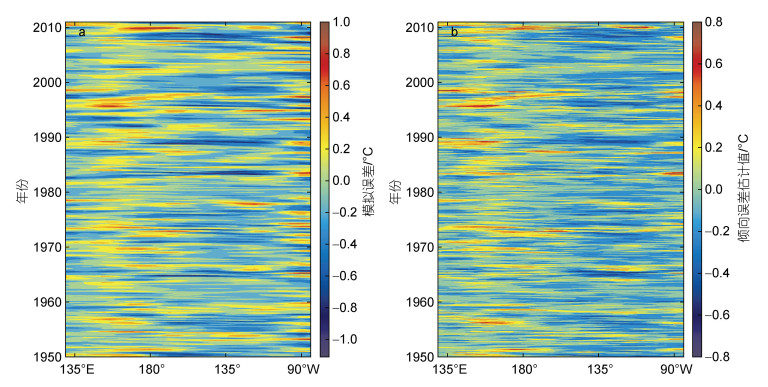 |
| 图 4 模拟误差(a)和模式倾向误差估计值(b)的时间-经度分布图 Fig. 4 Time-longitude distribution of the error (a) and the model tendency error estimates (b) |
对误差和模式倾向误差估计值进行经验正交函数(empirical orthogonal function, EOF)分解, 从而可以了解两场的时空演变特征。图 5为误差和模式倾向误差估计值EOF分解所得的4个主要特征模态的空间分布, 图 6则给出了对应的时间系数。从图 5a可以看出, 误差的第一特征模态呈东正西负的空间分布, 正值区主要出现在中部太平洋地区, 并逐渐向东、向赤道外扩散, 负值区在中、西部太平洋呈“马蹄形”环绕正值区。倾向误差估计值的第一特征模态(图 5e)也呈现了一个东正西负的分布, 正值主要集中在赤道附近的中、东部太平洋地区, 负值在北太平洋中部最大, 向西、向南逐渐减小, 整体呈现出一个类似El Niño事件分布的空间型, 与误差的第一特征模态具有相似的空间特征, 两场的相关系数达到了0.72。同样地, 从图 6a可见, 第一特征模态对应时间系数的相关高达0.87, 说明在时空两个维度, 两场的演变都是较为一致的。
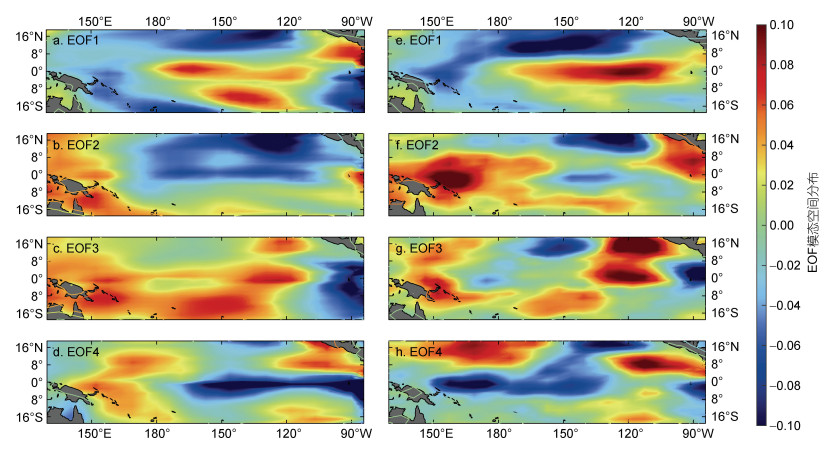 |
| 图 5 模拟误差(a, b, c, d)和倾向误差估计值(e, f, g, h) EOF分解所得的4个主要特征模态空间分布 Fig. 5 Spatial distribution of the four main EOF patterns of the error (a, b, c, d) and the tendency error estimates (e, f, g, h) 注:EOF1表示EOF分解的第一特征模态; EOF2表示EOF分解的第二特征模态; EOF3表示EOF分解的第三特征模态; EOF4表示EOF分解的第四特征模态 |
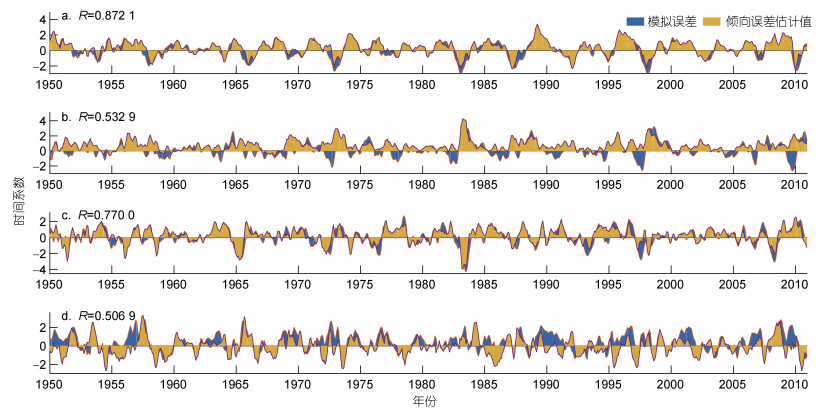 |
| 图 6 模拟误差和倾向误差估计值EOF分解所得的4个主要特征模态对应的时间系数 Fig. 6 The time coefficients corresponding to the four main EOF patterns of the error and the tendency error estimates 注: R表示相关系数 |
进一步比较第二、三、四特征模态, 可以看到, 误差的第二特征模态(图 5b)在西太平洋和北太平洋地区分别出现了较明显的正值和负值, 这些显著的特征在倾向误差估计值的第二特征模态(图 5f)也有所体现。此外, 两场的第三特征模态(图 5c和5g)空间分布高度相似, 自西向东依次呈现正、负、正、负的空间结构, 且两场的相关系数达到了0.58, 图 6c对应的时间序列相关为0.77。在第四特征模态(图 5d和5h)中, 误差场的负值集中在近赤道中、东部太平洋地区, 正值分布在西太平洋地区和赤道两侧, 呈现了类似La Niña事件的空间型, 而在估计值场中, 近赤道西太平洋地区出现了负值, 其他地区的空间分布均与误差场相似。总的来说, 四个特征模态的空间场和对应时间系数序列的相关均达到了0.5以上, 进一步论证了模式倾向误差估计值与误差之间的高度相关关系, 这体现了LETKF同化技术用于估计模式倾向误差的有效性。
2.2 考虑模式倾向误差的ENSO模拟上文分析了模式倾向误差估计值的时空特征, 揭示了其与模拟误差之间的高度相关关系。接下来, 展开ENSO模拟实验, 评估模式倾向误差估计在改善模式模拟效果方面的作用。将2.1.3中模式倾向误差EOF分解所得的4个主要空间模态, 在每一个时间步乘以一个随机的系数X[X~U(−1, 1)], 再进行加和, 将合成的空间场加入模式倾向方程。为了与ZC模式进行区分, 将带有模式倾向误差的ZC模式称为F-ZC模式。自由积分F-ZC模式150 a, 积分结果用来考察模式倾向误差估计对ENSO模拟的影响。
2.2.1 赤道地区海温距平场的时间–经度分布特征图 7为ZC模式和F-ZC模式自由积分的模拟结果沿赤道地区的时间-经度分布图。可以看出, ZC模式模拟的El Niño事件十分显著, 绝大多数事件的峰值高达4 ℃, 相对来说, 模拟的La Niña事件强度偏低, 出现不对称的振荡。F-ZC模式的模拟同样准确地模拟出了这种不对称性, 且第2.1.1节中提到, ZC模式在冷事件的模拟上常高于观测, 而F-ZC模式在一定程度上修正了这种高估, 其模拟的La Niña事件的强度和频率均有所增加。此外, ZC模式模拟的暖事件在空间形态分布上均呈现出EP型El Niño事件这一单一形态特征, 而F-ZC模式不仅模拟出了EP型El Niño事件, 也模拟出了类似于CP型El Niño事件的空间型, 如第14 a、第77 a和第98 a的三次模拟, 尽管强度较低, 但模拟结果呈现出多样性。
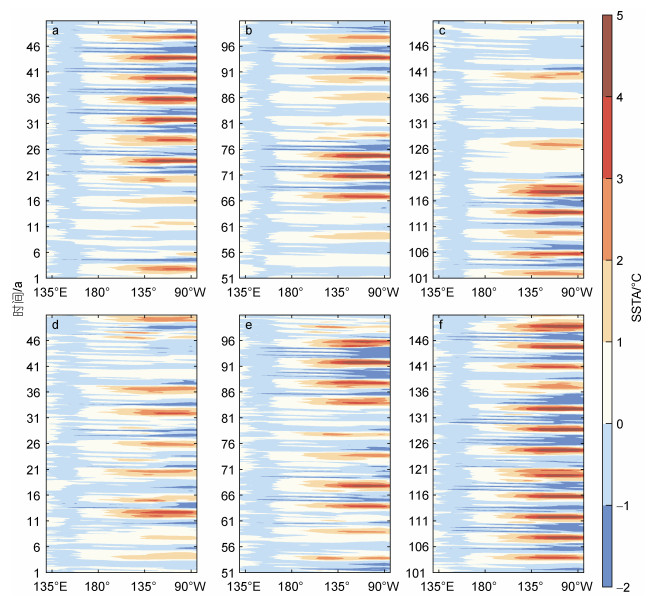 |
| 图 7 ZC模式(a, b, c)和F-ZC模式(d, e, f) 150 a自由积分模拟SSTA沿赤道纬圈的时间—经度分布图 Fig. 7 Time-longitude distribution along the equator of the 150-year free-integral simulated SSTA in ZC model (a, b, c) and F-ZC model (d, e, f) |
为了考察模式模拟ENSO周期的能力, 对Niño 3.4区SSTA时间序列进行功率谱分析, 并将其与观测进行对比。图 8a、8b、8c分别是SSTA观测值、ZC模式和F-ZC模式自由积分模拟结果的功率谱分析。整体上, 观测和两组模拟实验的周期均与通常所认为的ENSO 2~7 a的主要周期一致。具体地, 观测除存在3.63 a的显著周期外, 也显示了4.88 a的一个次要周期。而ZC模式和F-ZC模式的模拟结果都显示出一个明显的主周期, 分别为3.97和4.16 a, 在F-ZC模式中开展多次模拟实验, 模拟结果的主周期均稳定在4.16 a, 在观测所涵盖的范围内。且相比较之下, F-ZC模式模拟结果的主周期更加接近于观测的次要周期。
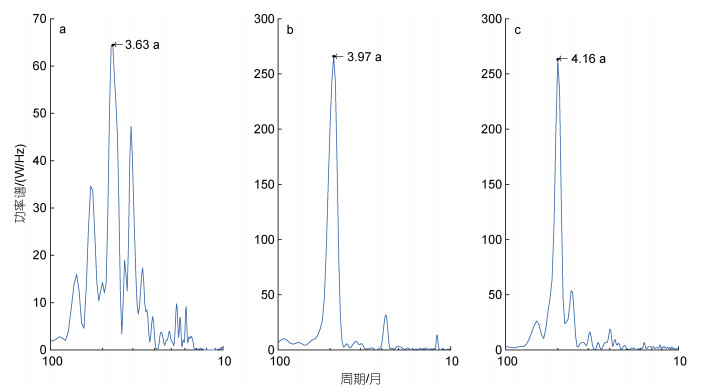 |
| 图 8 观测(a)、ZC模式(b)和F-ZC模式(c)模拟结果在Niño3.4区的SSTA时间序列功率谱 Fig. 8 The power spectrum of the SSTA time series in Niño3.4 zone of the observation (a), ZC model (b) and F-ZC model (c) |
除强度和周期外, ENSO的季节锁相也是衡量ENSO模拟效果的一个重要指标。尽管各个ENSO事件的振幅各不相同, 但ENSO相位非常相似, SSTA的峰值总是出现在冬季。为了更清楚地描述El Niño事件和La Niña事件的相位特征, 分别选取观测、ZC模式模拟和F-ZC模式模拟中显著的El Niño事件和La Niña事件进行合成(中华人民共和国国家质量监督检验检疫总局等, 2017)。
图 9a和9b分别绘制了暖事件和冷事件前后Niño3.4指数的时间演变, 其中, (0)年表示事件达到峰值的当年。从观测可以看到, 暖事件发生时, Niño3.4区域逐渐变暖, 从当年的春季开始进入El Niño事件, 在冬季12月份达到峰值, 之后逐渐减弱, 直至次年夏季事件结束。ZC模式模拟输出的El Niño事件峰值出现在当年的秋季9月份, 相比较之下, F-ZC模式模拟的El Niño事件峰值出现的时间更加接近于观测的峰值时间, 出现在冬季12月份。在事件强度方面, F-ZC模式模拟的事件强度整体上也是更接近于观测的, 尤其是在达到峰值前的事件发展期, ZC模式在当年年初就已经出现了一个中等强度的El Niño事件, F-ZC模式则表现更好。在冷事件的模拟上, 观测的峰值也出现在冬季12月份, 从当年年初开始变冷后, 在夏季发生La Niña事件, 逐步发展变强, 降至最低温之后开始升温, 直至次年夏季结束一次事件。但两个模式的模拟实验均未表现出明显的相位锁定, 均在当年的冬季和次年的夏季出现了两个不同的峰值, 且模拟的冷事件强度和持续时间都偏低。从整体趋势上看, F-ZC模式的模拟输出更接近于观测, 对次年夏季的第二次La Niña事件有一定程度的校正。重复开展多次模拟实验, 在季节锁相的模拟上, F-ZC模式表现均优于ZC模式。
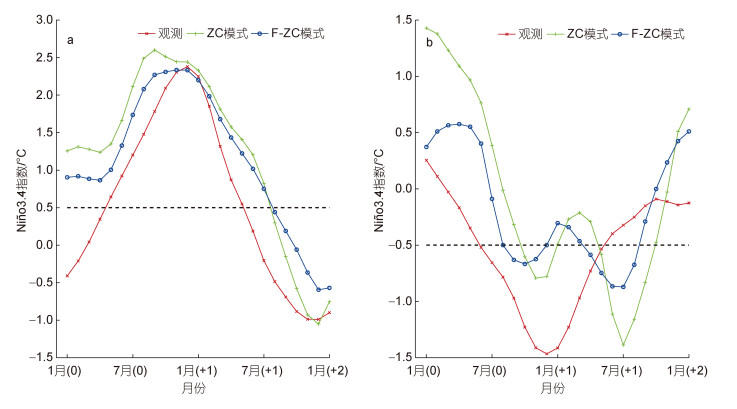 |
| 图 9 合成的El Niño事件(a)和La Niña事件(b)在Niño 3.4区的SSTA演变 Fig. 9 The evolution of SSTA in the Niño 3.4 region for composite El Niño events (a) and La Niña events (b) 注: (0)表示事件达到峰值的当年; (+1)表示次年; (+2)表示第三年 |
为了进一步比较模式对主要空间模态的模拟效果, 分别对观测的SSTA值、ZC模式和F-ZC模式模拟所得的SSTA分析值进行EOF分解, 图 10给出了观测及模式模拟的SSTA主要特征模态。由于自由积分模拟实验属于理想实验, 没有对应的真实时间, 因此, 这里仅比较主要空间模态的分布。
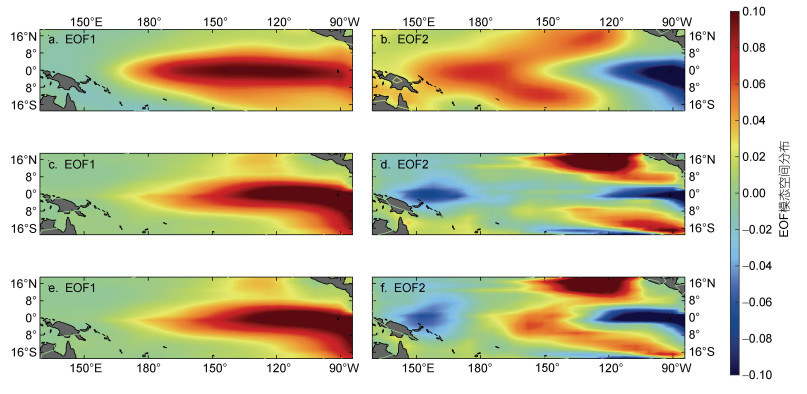 |
| 图 10 观测(a, b)、ZC模式(c, d)和F-ZC模式(e, f)模拟的SSTA值EOF分解的前两个主要特征模态空间分布 Fig. 10 The spatial distribution of the 1st and 2nd EOF patterns of the observed SSTA (a, b), the simulated SSTA in ZC model (c, d) and F-ZC model (e, f) 注: EOF1表示EOF分解的第一特征模态; EOF2表示EOF分解的第二特征模态 |
观测的SSTA第一特征向量(图 10a)呈东正西负的分布, 正值区从美洲西岸逐渐向西延伸到日界线附近, 而负值区则从西太平洋地区呈“C字型”向东北及东南延伸。这一模态与El Niño事件发生时的热带太平洋SSTA分布型相似, 可称为ENSO模态, 它可以解释SSTA总方差的72%。观测的第二特征模态(图 10b)与第一特征模态恰好相反, 是一个西部为正值而东部为负值的模态, 赤道西太平洋的正值最大并向东部延展, 赤道东太平洋的负值最大并向西部延展, 最终在中太地区相遇, 使从西太而来的正值扩散至南、北太平洋, 呈“树杈状”分布。
在模拟实验的SSTA场EOF分解中, ZC模式和F-ZC模式模拟的SSTA主要特征向量均与观测较为接近。可以看到, 两个模拟实验的第一特征模态(图 10c和10e)非常相似, 均为一个典型的中、东部型El Niño事件空间形态, 正值区从东南太平洋逐渐向西发展。同样, 和观测类似, 第一特征模态的贡献也是最大的, 分别达到了82%和78%, 这表明ZC模式能较好地模拟出ENSO事件最主要的形态特征, 同样加入了模式倾向误差参数的F-ZC模式仍保持住了这一优势。进一步比较第二特征模态(图 10d和10f), 发现ZC模式和F-ZC模式的模拟都表现出了从东太地区向西延展的负值, 与观测是一致的, 但两者均未模拟出从西太起逐步向东传播的正值。尽管如此, 与ZC模式相比, F-ZC模式弱化了在西太的负值, 强化了在中太的正值, 模拟出了更加接近观测的第二特征模态, 说明模式倾向误差的加入对ENSO模拟效果产生了正面影响。重复开展多次模拟实验, 实验结果稳定一致。
3 结论本研究基于ZC模式, 延续Roads等(Roads, 1987; Moore et al, 1999; Barkmeijer et al, 2003; Duan et al, 2013, 2014; Tao et al, 2019)将模式倾向误差视作模式参数的思想, 利用LETKF同化技术对模式倾向误差进行估计, 发展出一种新的模式倾向误差的计算方法。在这基础上, 基于1950~2020年的SSTA观测数据, 计算得到了对应于1950~2011年的模式倾向误差估计值。通过相关性分析和EOF分析发现, 模式倾向误差估计值和模拟误差之间具有高度相关关系。进一步地将倾向误差估计项加入ZC模式, 重复开展了多次ENSO模拟实验。通过与ZC模式的对比, 发现在150 a的自由积分实验中, 带有模式倾向误差的F-ZC模式均能进一步改善对ENSO事件的模拟效果, 在振幅、周期、相位锁定和主要空间形态等方面, 模拟与观测的相关性均有所提高。
本研究提出的这种新的估计模式倾向误差的方法, 计算简便高效, 可便捷地应用于其他模式中, 具有较高的推广应用价值。但不同模式中存在的倾向误差也是不同的, 尽管本方法在ZC模式中得到了较好的应用, 但在其他更为复杂的耦合模式中的应用效果如何, 仍需要进一步的工作来验证, 这也是本研究接下来的一个主要工作方向。而模式倾向误差估计方法存在的一些不足也有待改进, 比如参数估计中常常遇到的滤波发散问题。此外, 模拟的最终目的仍是为了提高预报效果, 该方法是否能用于提高ENSO的预报技巧, 仍有待检验。
王琳, 张灿影, 於维樱, 等, 2019. 厄尔尼诺-南方涛动(ENSO)研究的战略部署与研究热点. 世界科技研究与发展, 41(1): 32-43 |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会, 2017. 厄尔尼诺/拉尼娜事件判别方法: GB/T 33666-2017[S]. 北京: 中国标准出版社: 3.
|
连涛, 陈大可, 唐佑民, 2017. 2014~2016厄尔尼诺事件的机制分析. 中国科学: 地球科学, 47(9): 1014-1026 |
吴新荣, 2013. 耦合气候模式中的参数估计研究[D]. 广州: 中国科学院大学(南海海洋研究所): 7-12.
|
沈浙奇, 唐佑民, 高艳秋, 2016. 集合资料同化方法的理论框架及其在海洋资料同化的研究展望. 海洋学报, 38(3): 1-14 |
岳彩军, 陆维松, 李清泉, 等, 2004. Zebiak-Cane海气耦合模式研究进展. 热带气象学报, 20(6): 723-730 |
夏咏华, 2001. "厄尔尼诺"事件及其对气候和航海活动的影响[D]. 大连: 大连海事大学: 10-13.
|
徐辉, 2006. Zebiak-Cane ENSO预报模式的可预报性问题研究[D]. 北京: 中国科学院研究生院(大气物理研究所): 10-13.
|
穆穆, 任宏利, 2017. 2014~2016年超强厄尔尼诺事件研究及其预测给予我们的启示. 中国科学: 地球科学, 47(9): 993-995 |
BARKMEIJER J, IVERSEN T, PALMER T N, 2003. Forcing singular vectors and other sensitive model structures. Quarterly Journal of the Royal Meteorological Society, 129(592): 2401-2423 DOI:10.1256/qj.02.126 |
CANE M A, ZEBIAK S E, 1985. A theory for El Niño and the southern oscillation. Science, 228(4073): 1085-1087 |
CANE M A, ZEBIAK S E, DOLAN S C, 1986. Experimental forecasts of El Niño. Nature, 321(6073): 827-832 DOI:10.1038/321827a0 |
CHEN D K, CANE M A, 2008. El Niño prediction and predictability. Journal of Computational Physics, 227(7): 3625-3640 DOI:10.1016/j.jcp.2007.05.014 |
CHEN D K, CANE M A, KAPLAN A, et al, 2004. Predictability of El Niño over the past 148 years. Nature, 428(6984): 733-736 DOI:10.1038/nature02439 |
CHEN D K, CANE M A, ZEBIAK S E, et al, 1998. The impact of sea level data assimilation on the Lamont model prediction of the 1997/98 El Niño. Geophysical Research Letters, 25(15): 2837-2840 DOI:10.1029/98GL52186 |
CHEN D K, ZEBIAK S E, BUSALACCHI A J, et al, 1995. An improved procedure for EI Niño forecasting: implications for predictability. Science, 269(5231): 1699-1702 DOI:10.1126/science.269.5231.1699 |
CHEN D K, ZEBIAK S E, CANE M A, et al, 1997. Initialization and predictability of a coupled ENSO forecast model. Monthly Weather Review, 125(5): 773-788 DOI:10.1175/1520-0493(1997)125<0773:IAPOAC>2.0.CO;2 |
DUAN W S, TIAN B, XU H, 2014. Simulations of two types of El Niño events by an optimal forcing vector approach. Climate Dynamics, 43(5): 1677-1692 |
DUAN W S, ZHOU F F, 2013. Non-linear forcing singular vector of a two-dimensional quasi-geostrophic model. Tellus A: Dynamic Meteorology and Oceanography, 65(1): 18452 DOI:10.3402/tellusa.v65i0.18452 |
GAO Y Q, LIU T, SONG X S, et al, 2020. An extension of LDEO5 model for ENSO ensemble predictions. Climate Dynamics, 55(11/12): 2979-2991 |
GAO Y Q, TANG Y M, SONG X S, et al, 2021. Parameter estimation based on a local ensemble transform Kalman filter applied to El Niño–southern oscillation ensemble prediction. Remote Sensing, 13(19): 3923 DOI:10.3390/rs13193923 |
HU J Y, DUAN W S, 2016. Relationship between optimal precursory disturbances and optimally growing initial errors associated with ENSO events: implications to target observations for ENSO prediction. Journal of Geophysical Research: Oceans, 121(5): 2901-2917 DOI:10.1002/2015JC011386 |
HUANG B Y, THORNE P W, SMITH T M, et al, 2016. Further exploring and quantifying uncertainties for extended reconstructed sea surface temperature (ERSST) version 4 (v4). Journal of Climate, 29(9): 3119-3142 DOI:10.1175/JCLI-D-15-0430.1 |
HUNT B R, KOSTELICH E J, SZUNYOGH I, 2007. Efficient data assimilation for spatiotemporal chaos: a local ensemble transform Kalman filter. Physica D: Nonlinear Phenomena, 230(1/2): 112-126 |
MOORE A M, KLEEMAN R, 1999. Stochastic forcing of ENSO by the intraseasonal oscillation. Journal of Climate, 12(5): 1199-1220 DOI:10.1175/1520-0442(1999)012<1199:SFOEBT>2.0.CO;2 |
MU M, DUAN W S, CHEN D K, et al, 2015. Target observations for improving initialization of high-impact ocean-atmospheric environmental events forecasting. National Science Review, 2(2): 226-236 DOI:10.1093/nsr/nwv021 |
PERIGAUD C, DEWITTE B, 1996. El Niño-La Niña events simulated with Cane and Zebiak's model and observed with satellite or in situ data. Part I: model data comparison. Journal of Climate, 9(1): 66-84 DOI:10.1175/1520-0442(1996)009<0066:ENNESW>2.0.CO;2 |
QI Q Q, DUAN W S, ZHENG F, et al, 2017. On the "spring predictability barrier" for strong El Niño events as derived from an intermediate coupled model ensemble prediction system. Science China Earth Sciences, 60(9): 1614-1631 DOI:10.1007/s11430-017-9087-2 |
ROADS J O, 1987. Predictability in the extended range. Journal of the Atmospheric Sciences, 44(23): 3495-3527 DOI:10.1175/1520-0469(1987)044<3495:PITER>2.0.CO;2 |
RUCKSTUHL Y, JANJIĆ T, 2020. Combined state-parameter estimation with the LETKF for convective-scale weather forecasting. Monthly Weather Review, 148(4): 1607-1628 DOI:10.1175/MWR-D-19-0233.1 |
TANG Y M, SHEN Z Q, GAO Y Q, 2016. An introduction to ensemble-based data assimilation method in the earth sciences [M] // LEE D B, BURG T, VOLOS C. Nonlinear Systems: Design, Analysis, Estimation and Control. New York, USA: Intech: 153-187.
|
TAO L J, DUAN W S, 2019. Using a nonlinear forcing singular vector approach to reduce model error effects in ENSO forecasting. Weather and Forecasting, 34(5): 1321-1342 DOI:10.1175/WAF-D-19-0050.1 |
WU X R, HAN G J, ZHANG S Q, et al, 2016. A study of the impact of parameter optimization on ENSO predictability with an intermediate coupled model. Climate Dynamics, 46(3/4): 711-727 |
YEH S W, KUG J S, DEWITTE B, et al, 2009. El Niño in a changing climate. Nature, 461(7263): 511-514 DOI:10.1038/nature08316 |
ZEBIAK S E, CANE M A, 1987. A model El Niño–southern oscillation. Monthly Weather Review, 115(10): 2262-2278 DOI:10.1175/1520-0493(1987)115<2262:AMENO>2.0.CO;2 |
ZHENG F, WANG H, ZHU J, 2009. ENSO ensemble prediction: initial error perturbations vs. model error perturbations. Chinese Science Bulletin, 54(14): 2516-2523 DOI:10.1007/s11434-009-0179-2 |
 2022, Vol. 53
2022, Vol. 53


