中国海洋湖沼学会主办。
文章信息
- 张弼强, 陆化杰, 赵懋林, 孙天姿, 郭瑞玉. 2023.
- ZHANG Bi-Qiang, LU Hua-Jie, ZHAO Mao-Lin, SUN Tian-Zi, GUO Rui-Yu. 2023.
- 基于GAM模型西北印度洋鸢乌贼CPUE标准化
- STANDARDIZATION OF CATCH PER UNIT EFFORT (CPUE) IN NORTHWEST INDIAN OCEAN STHENOTEUTHIS OUALANIENSIS BASED ON GENERALIZED ADDITIVE MODEL
- 海洋与湖沼, 54(1): 259-265
- Oceanologia et Limnologia Sinica, 54(1): 259-265.
- http://dx.doi.org/10.11693/hyhz20220400112
文章历史
-
收稿日期:2022-04-27
收修改稿日期:2022-07-06
2. 自然资源部海洋生态监测与修复技术重点实验室 上海 201306;
3. 国家远洋渔业工程技术研究中心 上海海洋大学 上海 201306;
4. 农业农村部大洋渔业资源环境科学观测实验站 上海海洋大学 上海 201306
2. Key Laboratory of Marine Ecological Monitoring and Restoration Technologies, MNR, Shanghai 201306, China;
3. National Distant-water Fisheries Engineering Research Center, Shanghai Ocean University, Shanghai 201306, China;
4. Key Laboratory of Oceanic Fisheries Exploration, Ministry of Agriculture and Rural Affairs, Shanghai Ocean University, Shanghai 201306, China
鸢乌贼(Sthenoteuthis oualaniensis)属枪形目(Teuthoidea)、柔鱼科(Ommastrephidae)、鸢乌贼属(Sthenoteuthis), 为一种暖水性的大洋性头足类, 主要分布于太平洋的赤道、印度洋和亚热带海域(董正之等, 1988; 赵荣兴, 1992; 杨德康, 2002)。鸢乌贼的经济捕捞价值较高, 是灯光罩网渔业重要的捕捞对象(陆化杰等, 2014), 其中在西北印度洋和我国南海资源量较为丰富(陈新军等, 2005; 范江涛等, 2022)。CPUE是指单位捕捞努力量渔获量(Catch Per Unit Effort, CPUE), 是进行渔业资源评估的重要因子(Hilborn et al, 1992; 何珊等, 2018), 广泛应用于渔业资源评估与管理中(Ault, 2000)。在实际应用中, 名义CPUE (未进行标准化的CPUE)受到捕捞时间、捕捞方式、渔船的参数、时空因子和海洋环境因子等多种因素的影响(Harley et al, 2001; Maunder et al, 2003), 难以保证其能够准确反映资源量(Ye et al, 2009)。鉴于此, 为了科学利用CPUE数据, 准确进行资源评估, 去除相关因素的影响, 常常需要对名义CPUE进行标准化(官文江等, 2014a)。
目前, 广义线性模型、广义加性模型、回归树模型、神经网络模型和栖息地模型等都是CPUE标准化的常用方法(Venables et al, 2004; 官文江等, 2014b)。广义可加模型(generalized additive model, GAM)作为广义线性模型(generalized linear model, GLM)的拓展, 可以利用样条平滑函数增加更多泰勒级数项(即多项式项), 使得模型成为非线性模型, 从而可以处理响应变量与多个解释变量之间的非线性关系, 目前在渔业资源等方面的研究中得到了广泛应用(陆化杰等, 2013a; 徐洁等, 2015)。本研究根据中国罩网渔船于2016~2020年西北印度洋鸢乌贼生产数据, 利用GAM模型对西北印度洋鸢乌贼渔业CPUE标准化进行研究, 旨在为后续资源评估和渔情预报等提供科学依据。
1 材料与方法 1.1 数据来源本研究中渔业数据来源于2016~2020年上海海洋大学鱿钓技术组, 调查范围为55°~70°E, 10°~22°N海域, 渔业数据包括作业渔船名、渔船作业时间、渔船作业经纬度、渔获产量等信息。针对渔业数据进行整体评估、分析, 选取月份为时间分辨率, 按照渔船实际作业区域划分渔区, 0.5°×0.5° (即一个渔区)为空间分辨率。
研究中涉及的环境因子主要包括海表盐度(sea surface salinity, SSS)、海表叶绿素a浓度(chl a)、海面高度(sea surface height, SSH)和海表面温度(sea surface temperature, SST), 这些环境因子与鸢乌贼CPUE变化密切相关。环境数据来源于ERDDAP-Home Page (hawaii.edu)以及https://oceandata.sci.gsfc.nasa.gov, 时间分辨率为月, 空间分辨率0.1°×0.1°。
1.2 数据处理由于渔业数据与环境数据的空间分辨率不同, 所以通过数理统计方法对环境数据与渔业数据按渔区进行统计(0.5°×0.5°), 计算每个渔区的月平均值, 对二者的空间分辨率进行转化, 确保渔业数据和环境数据在空间分辨率上的一致。
本文将CPUE的定义为每艘船每次作业的捕捞产量, CPUEy, m, k, l表示第y年、m月、k经度、l纬度(分辨率为0.5°×0.5°) CPUE的平均值:
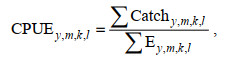 (1)
(1)式中, ∑Catchy, m, k, l为第y年、m月、k经度、l纬度所有渔船的总渔获量(kg), ∑Ey, m, k, l为对应作业区域的总作业天数(单位: d)(田思泉等, 2010)。
海表面温度计算公式如下:
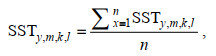 (2)
(2)式中, ∑SSTy, m, k, l为第y年、m月、k经度、l纬度(0.5°×0.5°)内SST的平均值, 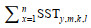
海表叶绿素a浓度计算公式如下:
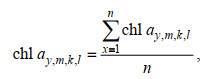 (3)
(3)式中, chl ay, m, k, l为第y年、m月、k经度、l纬度(0.5°×0.5°)内chl a浓度的平均值; 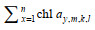
海表面盐度计算公式如下:
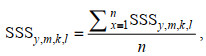 (4)
(4)式中, SSSy, m, k, l为第y年、m月、k经度、l纬度渔区(0.5°×0.5°)内SSS的平均值, 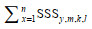
海面高度计算公式如下:
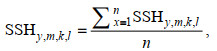 (5)
(5)式中, SSHy, m, k, l为第y年、m月、k经度、l纬度(0.5°×0.5°)内SSH的平均值, 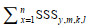
对于处理好的CPUE数据以及环境数据, 利用EXCEL软件和R语言软件按照相同的时空分辨率对二者进行匹配。当环境数据缺失时, 舍弃当天对应区域的生产数据。
1.3 分析方法在本研究中采用GAM模型对印度洋鸢乌贼CPUE进行标准化处理, 以CPUE作为响应变量, 而月份、作业经度、作业纬度、海表温度、叶绿素a浓度、海表盐度、海面高度作为其解释变量建立GAM模型, 对所有的名义CPUE值加上常数“1”后进行对数化处理, 防止CPUE为0的情况出现(陆化杰等, 2013b), 其表达式为:
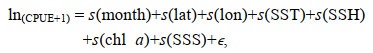 (6)
(6)式中, s为自然样条平滑函数, lat表示纬度, lon表示经度, month表示月份, SST表示海表温度, chl a表示叶绿素a浓度, ϵ表示随机变量。
对于模型的检验, 则是可以利用赤池信息准则(Akaike information criterion, AIC)检验加入因子后模型的拟合程度, AIC值越小, 模型的拟合程度越高。
其次, 利用F值、P值检验因子在模型中的显著与否(Akaike, 1974; 宋利明等, 2013)。
2 结果 2.1 因子的显著性检验利用GAM模型对各因子进行显著性检验, 结果表明, 月份、经度、纬度、SST、SSH对CPUE的影响显著(P < 0.05), 为显著性变量, SSS及chl a对CPUE的影响不显著(P > 0.05)。从表 2来看, 将经度、纬度、月份、SST以及SSH加入模型后, 模型的偏差解释率得到明显提升, 而当模型中加入chl a以及SSS时, 模型的偏差解释率并没有显著性增加, 甚至有所降低, 而且其AIC值增加, R2值减小, 所以将经度、纬度、月份、SST及SSH这5个因子保留, 剔除SSS和chl a这两个因子。最终优化模型为
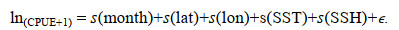 (7)
(7)| 因子 | F | P |
| s(lon) | 12.535 | < 2e-16*** |
| s(lat) | 4.381 | 1.45e-05*** |
| s(month) | 6.585 | < 2e-16*** |
| s(SST) | 4.019 | 1.64e-05*** |
| s(chl a) | 0.931 | 0.346 1 |
| s(SSS) | 0.487 | 0.705 7 |
| s(SSH) | 1.867 | 0.049 2* |
| 注: ***表示P < 0.001; *表示P < 0.05 | ||
| 模型公式 | AIC | 累计解释偏差 | 决定系数R2 |
| ln(CPUE+1)=s(lon) | 2 044.611 | 24.7% | 0.235 |
| ln(CPUE+1)=s(lon)+s(lat) | 2 020.813 | 28.4% | 0.267 |
| ln(CPUE+1)=s(lon)+s(lat)+s(month) | 1 982.103 | 33.9% | 0.317 |
| ln(CPUE+1)=s(lon)+s(lat)+s(month)+s(SST) | 1 955.292 | 39.0% | 0.357 |
| ln(CPUE+1)=s(lon)+s(lat)+s(month)+s(SST)+s(SSH) | 1 948.895 | 40.3% | 0.367 |
| ln(CPUE+1)=s(lon)+s(lat)+s(month)+s(SST)+s(SSH)+s(SSS) | 1 950.587 | 40.4% | 0.366 |
| ln(CPUE+1)=s(lon)+s(lat)+s(month)+s(SST)+s(SSH)+s(chl a) | 1 950.325 | 40.2% | 0.366 |
| ln(CPUE+1)=s(lon)+s(lat)+s(month)+s(SST)+s(SSH)+s(chl a)+s(SSS) | 1 952.15 | 40.3% | 0.365 |
最终优化模型对CPUE总偏差解释率为40.3%, 在构成模型的因子中经度对CPUE的影响最大, 其解释偏差率最高为24.7%, 其次分别为月份(5.5%)、SST (5.1%)、纬度(3.7%)和SSH (1.3%)。
2.2 空间因子对于CPUE的影响在所有因子中, 经度的方差解释率最高, 为24.7%。从图 1中可知, 在60°E以西, 随着经度的逐步增加, 西北印度洋海域鸢乌贼CPUE呈现出逐步增长的趋势。随后在60°~65°E, CPUE变化不明显, 在65°E以东, CPUE又呈现出随经度的增加而降低的趋势。纬度的方差解释率为3.7%, 从图 2中可以看到, 在10°~14°N随着纬度向北逐渐增加, CPUE总体上逐步减少。但在14°~16°N, 伴随着纬度的增加, CPUE随之缓慢增加。随后在16°~19°N范围内, CPUE随着纬度的增加有缓慢减小的趋势。在19°N以北范围内, 随着纬度的增大, CPUE呈增大的趋势。结合图 1以及图 2来看, 在经度上, 58°E以西范围和66°E以东范围内的数据量较小, 其置信区间范围较大; 在纬度上, 12°E以南范围和20°N以北范围内的置信区间范围较大, 其可信度相对较低, 鉴于此, 高CPUE的空间分布海域范围为14°~19°N、60°~65°E。
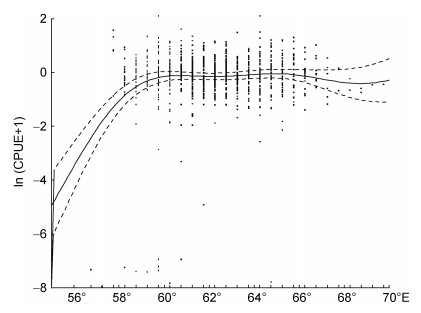 |
| 图 1 GAM模型中经度对鸢乌贼CPUE的影响 Fig. 1 Effect of longitude on CPUE of S. oualaniensis in GAM model |
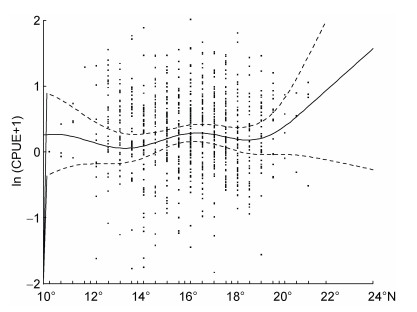 |
| 图 2 GAM模型中经度对鸢乌贼CPUE的影响 Fig. 2 Effect of longitude on CPUE of S. oualaniensis in GAM model |
在所有模型因子中, 月份的方差解释率位居第二, 为5.5%。从图 3中可以看出, 1~3月、5~10月的范围内, 随着时间的增加, CPUE呈逐步增长趋势。而在3~5月、10~12月的范围内, 随着时间的增加, CPUE呈递减趋势。在所有月份中, 10月份的CPUE最高。
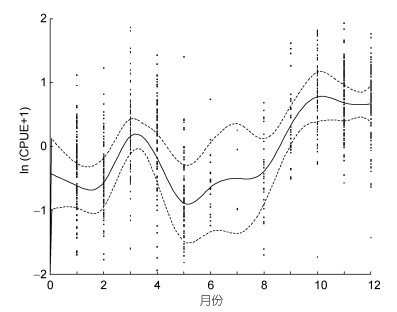 |
| 图 3 GAM模型中月份对鸢乌贼CPUE的影响 Fig. 3 Effect of month on CPUE of S. oualaniensis in GAM model |
海表温度和海面高度的方差解释率分别为5.1%和1.3%。西北印度洋鸢乌贼作业海域的海表温度范围为24.0~30.5 ℃。从图 4可知, 当SST在24~25 ℃之间时, CPUE随SST的增加呈上升趋势, 在25 ℃时CPUE最大。而SST在25~28 ℃范围内时, 随着SST的增加CPUE呈现递减的趋势, 28 ℃时CPUE最小。SST在28~30.5 ℃范围内时, 随着SST的增加, CPUE也逐步增加。在西北印度洋鸢乌贼作业海域, 海面高度的范围为0.15~0.67 m。由图 5可知, 当SSH在0.15~0.30 m范围内时, CPUE随着SSH的增加而逐步减少。当SSH在0.30~0.67 m范围时, CPUE随着SSH的增加呈现先增加后减少的趋势, 在SSH等于0.4 m时, CPUE上升到顶点。SSH在0.5~0.67 m的范围内, 数据量较为少, 置信区间较大, 所以其可信度相对而言较低。
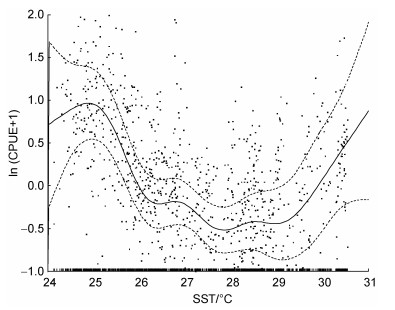 |
| 图 4 GAM模型中SST对鸢乌贼CPUE的影响 Fig. 4 Effect of SST on CPUE of S. oualaniensis in GAM model |
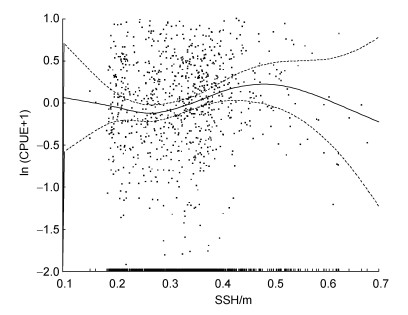 |
| 图 5 GAM模型中SSH对鸢乌贼CPUE的影响 Fig. 5 The effect of SSH on CPUE of S. oualaniensis in GAM model |
从图 6可知, 2016~2020年的9月到翌年3月期间, 名义CPUE与标准化后CPUE均维持在较高水平, 2020年4~8月期间, 名义CPUE与标准化CPUE均呈现下降趋势。从整体上来看, 除部分年间的月份外, 名义CPUE均高于标准化CPUE。尽管在各个月份之间, CPUE均有一定变化, 但相较而言标准化后CPUE变化波动较小, 而名义CPUE的变化波动较大, 各个月份的名义CPUE与标准化后的CPUE变化趋势基本一致。
 |
| 图 6 2016~2020年西北印度洋鸢乌贼月平均名义CPUE与标准化CPUE的关系 Fig. 6 Relationship between monthly average nominal CPUE and standardized CPUE of S. oualaniensis in the northwest Indian Ocean from 2016 to 2020 |
时空因子(经度、纬度等)和环境因子(SST、SSH等)的变化都会影响到西北印度洋鸢乌贼资源的分布(陈新军等, 2005)。在本研究中, GAM模型由纬度、经度、月份、SST、SSH这几个因子构成。陆化杰等(2013c)在基于GAM模型对西南大西洋的阿根廷滑柔鱼CPUE标准化研究中, 对CPUE总偏差的解释为49.20%, 许骆良等(2015)基于GAM模型分析了秘鲁外海茎柔鱼的资源丰度变化时对CPUE进行标准化, 其方差解释率为42.3%, 其他学者(陆化杰等, 2013c; 谢恩阁等, 2020)利用GAM模型进行CPUE标准化的总偏差解释率范围为30%~70%。本文采用GAM模型对CPUE进行标准化, 其总偏差解释率为40.3%, 相对可信度较高。
3.1 时空因子对CPUE的影响本研究结果表明经度、纬度、月份对CPUE解释的总偏差解释率为33.9%。从空间因子来看, 在经度方面, 伴随着经度的增加, CPUE整体上呈现出递增趋势, 在纬度方面, 随着纬度的增加, CPUE的值也不断增大。通过排除可信度较低的部分, 将二者结合显示, 在16°~19°N、60°~65°E的海域, 西北鸢乌贼的CPUE相对较大。这与陈新军等(2006)通过分析CPUE的空间分布与环境之间的关系, 判断西北印度洋海域鸢乌贼高产渔场的分布范围位于16°~19°N, 60°~63°E海域的结论基本上一致。从时间因子(月份)的变化情况来看, 上半年鸢乌贼的CPUE低于下半年, 其中CPUE最低的季度是第3季度(7~9月), CPUE最高的季度是第4季度(10~12月)。产生这种情况的原因有很多, 其中包括不同季度环境因子的变化等(周天军等, 2004)。CPUE最高的月份为10月份, 最低月份为7月份, 除此之外可以看到9月~翌年3月份西北印度洋海域鸢乌贼的产量以及CPUE均维持在较高水平, 本文研究认为9月至翌年3月为西北印度洋海域鸢乌贼的生产鱼汛。林东明等(2006)认为西北印度洋海域的鸢乌贼生产渔汛为9月至翌年的4月, 杨德康(2002)则是根据渔船生产的经验, 认为位于亚丁湾的鸢乌贼渔场其渔汛期为10月至翌年的2月份。与本文研究结果并不完全相同, 原因主要是渔业生产作业的海域不同, 林东明等(2006)研究针对的海域范围为10.5°~22.5°N、54.5°~67.5°E, 而杨德康(2002)研究的作业海域为近海, 本文研究的海域范围为55°~70°E、10°~22°N。
3.2 环境因子对CPUE的影响在本研究中, 环境因子中海表温度以及海面高度对西北印度洋鸢乌贼CPUE呈显著性影响。SST作为影响鸢乌贼CPUE的最大环境因素, 许多学者研究证实了SST对于头足类渔场分布有着重要的影响作用(温健等, 2019; 李杰等, 2020)。本研究结果表明, 西北印度洋鸢乌贼的适宜SST为25~29 ℃, 其中主要分布在SST为25~28 ℃范围内的海域, 在这个海域内鸢乌贼的产量和CPUE均较高。林东明等(2006)调查表明鸢乌贼渔场最适SST为25~26 ℃以及27~28 ℃的海域, 余为等(2012)认为鸢乌贼渔场最适SST范围27~29 ℃, 这与本文结论有部分差异, 范江涛等(2015)同样认为不同季节, 鸢乌贼分布的最适SST不同, 这可能主要是由于所调查的作业渔场经纬度范围以及作业时间(月份)的不同导致的。
相关学者研究认为, 海面高度与水文特征、营养物质、饵料等息息相关, 对中上层鱼类的生长、繁殖以及空间分布等存在一定影响(邵锋等, 2008)。在GAM模型结果中, SSH因子对于CPUE呈显著性影响, 本次研究得到西北印度洋鸢乌贼渔场的最适SSH范围为0.2~0.4 m, 谢恩阁等(2020)通过对于南海鸢乌贼灯光罩网CPUE标准化研究, 分析认为其最适海面高度为0.60~0.75 m, 余为等(2012)认为的印度洋鸢乌贼渔场适宜的SSH为0.23~0.32 m, 本研究与余为等(2012)的研究结果更加接近, 究其原因还是研究海域的不同引起的, 余为等(2012)研究的海域主要位于2°~24°N、57°~69°E, 本文研究的海域范围为55°~70°E、10°~22°N, 也可能还是由于数据的时空尺度以及地理范围上存在差异引起的。
3.3 名义CPUE与标准化CPUE的比较本研究表明, 西北印度洋鸢乌贼名义CPUE大部分要高于标准化CPUE, 这一点与其他学者(田思泉等, 2010; 陆化杰等, 2013c)利用GAM模型处理CPUE标准化的结果基本一致。虽然二者总体上的变化趋势大体相同, 但标准化CPUE相较名义CPUE变化幅度较小, 名义CPUE的变化起伏较大, 即利用GAM模型处理后的标准化CPUE, 在一定程度上能够排除模型中时空因子和环境因子对于名义CPUE的影响, 对于之后的资源评估和渔情预报等提供更加准确的科学依据(官文江等, 2014a; 马亚宸等, 2021)。陆化杰等(2013c)利用GAM模型对西南大西洋阿根廷滑柔鱼CPUE标准化中, 就月平均CPUE而言, 名义CPUE与标准化CPUE变化趋势更加吻合。究其原因, 其GAM模型中环境因子以及时空因子更多, 这也是和所研究物种和地域的不同有关。章贤成等(2022)利用BP神经网络对西南大西洋阿根廷滑柔鱼资源CPUE标准化研究中, 名义CPUE与标准化CPUE存在一定的差别, 在变化趋势上二者呈现出一致性, 这与模型的选择有很大的关系。
4 结论本文通过GAM模型对影响CPUE的相关因子进行筛选, 确认模型中的显著变量, 对CPUE进行标准化处理。分析了各个因子与CPUE以及渔获量之间的关系, 研究结果认为在9月至翌年3月, 经纬度为16°~19°N、60°~65°E, SST为25~28 ℃、SSH为0.2~0.4 m的海域为高渔获量、高CPUE海域。标准化CPUE始终低于名义CPUE, 但二者的分布趋势基本一致。在GAM模型的基础上, 针对西北印度洋鸢乌贼的CPUE标准化, 相对能够更加准确地反映了西北印度洋鸢乌贼资源的变化情况, 为后续的资源评估和渔情预报提供了科学依据。
马亚宸, 徐宾铎, 张崇良, 等, 2021. 黄渤海蓝点马鲛双船拖网渔业CPUE时空变化及其标准化. 中国水产科学, 28(4): 493-502 |
田思泉, 陈新军, 2010. 不同名义CPUE计算法对CPUE标准化的影响. 上海海洋大学学报, 19(2): 240-245 |
许骆良, 陈新军, 汪金涛, 2015. 2003-2012年秘鲁外海茎柔鱼资源丰度年间变化分析. 上海海洋大学学报, 24(2): 280-286 |
李纲, 陈新军, 田思泉, 2009. 我国东、黄海鲐鱼灯光围网渔业CPUE标准化研究. 水产学报, 33(6): 1050-1059 |
李杰, 张鹏, 晏磊, 等, 2020. 南海中南部海域鸢乌贼CPUE影响因素的GAM分析. 中国水产科学, 27(8): 906-915 |
杨德康, 2002. 两种鱿鱼资源和其开发利用. 上海水产大学学报, 11(2): 176-179 |
何珊, 王学昉, 戴黎斌, 等, 2018. 人工集鱼装置禁渔期措施对中国大陆金枪鱼围网船队捕捞努力量特征的影响. 大连海洋大学学报, 33(1): 102-107 |
余为, 陈新军, 2012. 印度洋西北海域鸢乌贼9-10月栖息地适宜指数研究. 广东海洋大学学报, 32(6): 74-80 DOI:10.3969/j.issn.1673-9159.2012.06.014 |
宋利明, 武亚苹, 2013. 基于GAM的吉尔伯特群岛海域黄鳍金枪鱼栖息地综合指数. 水产学报, 37(8): 1250-1261 |
陆化杰, 王从军, 陈新军, 2014. 4-6月东太平洋赤道公海鸢乌贼生物学特性初步研究. 上海海洋大学学报, 23(3): 441-447 |
陆化杰, 陈新军, 方舟, 2013a. 西南大西洋阿根廷滑柔鱼渔场时空变化及其与表温的关系. 海洋渔业, 35(4): 382-388 |
陆化杰, 陈新军, 曹杰, 2013b. 基于GLBM模型的中国大陆阿根廷滑柔鱼鱿钓渔业CPUE标准化. 生态学报, 33(17): 5375-5384 |
陆化杰, 陈新军, 曹杰, 等, 2013c. 中国大陆阿根廷滑柔鱼鱿钓渔业CPUE标准化. 水产学报, 37(6): 951-960 |
陈新军, 叶旭昌, 2005. 印度洋西北部海域鸢乌贼渔场与海洋环境因子关系的初步分析. 上海水产大学学报, 14(1): 55-60 |
陈新军, 邵锋, 2006. 印度洋西北部公海鸢乌贼资源特征及其与海况的关系. 中国海洋大学学报, 36(4): 611-616 |
邵锋, 陈新军, 2008. 印度洋西北海域鸢乌贼渔场分布与海面高度的关系. 海洋科学, 32(11): 88-92 |
范江涛, 余为, 马胜伟, 等, 2022. 春季南海鸢乌贼栖息地时空分布及其年际差异分析. 南方水产科学, 18(1): 1-9 |
范江涛, 张俊, 冯雪, 等, 2015. 基于栖息地模型的南沙海域鸢乌贼渔情预报研究. 南方水产科学, 11(5): 20-26 |
林东明, 陈新军, 2006. 印度洋西北部海域鸢乌贼渔场分布及其与海面温度的关系. 海洋科学进展, 24(4): 546-551 |
周天军, 俞永强, 宇如聪, 等, 2004. 印度洋对ENSO事件的响应: 观测与模拟. 大气科学, 28(3): 357-373 |
官文江, 田思泉, 王学昉, 等, 2014a. CPUE标准化方法与模型选择的回顾与展望. 中国水产科学, 21(4): 852-862 |
官文江, 陈新军, 高峰, 等, 2014b. GLM模型和回归树模型在CPUE标准化中的比较分析. 上海海洋大学学报, 23(1): 123-130 |
赵荣兴, 1992. 印度洋可开发的外洋性头足类. 现代渔业信息, 7(8): 25-26 |
徐洁, 官文江, 陈新军, 2015. 基于空间相关性的西北太平洋柔鱼CPUE标准化研究. 水产学报, 39(5): 754-760 |
章贤成, 汪金涛, 陈新军, 2022. 基于BP神经网络的阿根廷滑柔鱼资源CPUE标准化研究. 渔业科学进展, 43(2): 11-20 |
董正之, 郑元甲, 朱善央, 1988. 东海南部的头足类稚仔. 水产学报, 12(1): 51-55 |
温健, 陆鑫一, 陈新军, 等, 2019. 基于海表温度和光合有效辐射的西北太平洋柔鱼冬春生群体栖息地热点预测. 上海海洋大学学报, 28(3): 456-463 |
谢恩阁, 周艳波, 冯菲, 等, 2020. 中国南海外海鸢乌贼灯光罩网渔业CPUE标准化研究. 大连海洋大学学报, 35(3): 439-446 |
AKAIKE H T, 1974. A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19(6): 716-723 |
AULT J S, 2000. Quantitative fish dynamics. Terrance J. Quinn Ⅱ, Richard B. Deriso. Quarterly Review of Biology, 75(3): 336 |
HARLEY S J, MYERS R A, DUNN A, 2001. Is catch-per-unit-effort proportional to abundance?. Canadian Journal of Fisheries and Aquatic Sciences, 58(9): 1760-1772 |
HILBORN R, WALTERS C J, 1992. Quantitative fisheries stock assessment: choice, dynamics and uncertainty. Reviews in Fish Biology and Fisheries, 2(2): 177-178 |
MAUNDER M N, STARR P J, 2003. Fitting fisheries models to standardised CPUE abundance indices. Fisheries Research, 63(1): 43-50 |
VENABLES W N, DICHMONT C M, 2004. GLMs, GAMs and GLMMs: an overview of theory for applications in fisheries research. Fisheries Research, 70(2/3): 319-337 |
YE Y M, DENNIS D, 2009. How reliable are the abundance indices derived from commercial catch-effort standardization?. Canadian Journal of Fisheries and Aquatic Sciences, 66(7): 1169-1178 |
 2023, Vol. 54
2023, Vol. 54


