
中国海洋湖沼学会主办。
文章信息
- 李博, 蔡华阳, 杨昊, 王博芝, 刘锋, 魏稳, 欧素英. 2023.
- LI Bo, CAI Hua-Yang, YANG Hao, WANG Bo-Zhi, LIU Feng, WEI Wen, OU Su-Ying. 2023.
- 珠江河网横向汊道水位演变特性及原因探究
- MECHANISM AND EVOLUTION OF WATER LEVEL CHANGES IN THE TRANSVERSE CHANNEL SYSTEM IN THE ZHUJIANG (PEARL) RIVER CHANNEL NETWORKS
- 海洋与湖沼, 54(2): 313-330
- Oceanologia et Limnologia Sinica, 54(2): 313-330.
- http://dx.doi.org/10.11693/hyhz20220600164
文章历史
-
收稿日期:2022-06-22
收修改稿日期:2022-08-25
2. 河口水利技术国家地方联合工程实验室 广东广州 510275;
3. 广东省海岸与岛礁工程技术研究中心 广东广州 510275;
4. 南方海洋科学与工程广东省实验室(珠海) 广东珠海 519000
2. State and Local Joint Engineering Laboratory of Estuarine Hydraulic Technology, Guangzhou 510275, China;
3. Guangdong Provincial Engineering Research Center of Coasts, Islands and Reefs, Guangzhou 510275, China;
4. Southern Laboratory of Ocean Science and Engineering (Zhuhai), Zhuhai 519000, China
河网区河道纵横交错, 主干道常分离出次级支流形成横向汊道, 常见于河口三角洲及其附近的冲积平原。在珠江三角洲, 由于其横向连结河控型“河道”和潮控型“潮道”, 因此, 形成独特的地貌和径潮耦合动力结构。独特的地貌动力结构决定其独特的动力功能, 如泄洪纳潮、潮能耗散、径潮动力耦合与转换功能。横向汊道体系对于保持河网的径潮动力平衡具有重要作用, 洪季该体系通过排泄洪流、缩短洪水位集中期, 减轻主河道的泄洪压力, 而枯季则通过增大河网区的纳潮量, 使潮能快速耗散, 并保证通航水深(何为, 2012)。横向汊道日均水位作为指示该地貌结构径潮动力格局的重要参数, 对其时空变化过程及主控影响因子的辨识, 不仅是河口动力学研究的重要内容, 亦是探讨横向汊道体系动态平衡及演变趋势的重要科学问题。
河口日均水位变化受到流量、地形、海平面变化和人类活动等多种驱动力影响, 导致其时空演变错综复杂。由于河口日均水位与径潮相互作用密切相关, 其时空演变对盐淡水混合、泥沙输运、地形地貌、生态系统等均有直接而显著的影响。以余水位及其梯度为切入点探讨横向汊道径潮动力变化特征及其独特的动力功能, 已有丰硕研究成果(Buschman et al, 2009; Cai et al, 2014; Alebregtse et al, 2016)。在复杂河网中, 纵向河道与横向汊道的余水位及其梯度将直接影响分汊口处的流量和潮能分配(刘俊勇, 2014), 作为连接河控型主干道和潮汐通道的过渡地带, 横向汊道余水位及其梯度的多时空尺度变化是影响感潮河段径潮动力结构的重要因素(Hoitink et al, 2017)。对河口地形进行概化并考虑下泄径流影响, 采用一维潮波传播解析模型可通过余水位梯度等参数揭示潮波传播的时空变化特征及其动力学机制(Cai et al, 2016)。当河口动力以径流作用为主时, 传统潮汐调和分析(Pawlowicz et al, 2002)的水位预报误差明显增大。针对流量影响下河口余水位时空演变的非平稳和非线性问题, 对水位或流量序列采用连续小波变换(Guo et al, 2015; Moftakhari et al, 2016)、经验模态分解(Pan et al, 2018a)、经验正交函数(Pan et al, 2019)、非平稳潮汐调和分析(Matte et al, 2013, 2014; Pan et al, 2018b)、傅里叶变换等处理方法探讨流量、地形、海平面等对余水位及其梯度的形成演变过程及机制取得较好效果。
强人类活动驱动下珠江三角洲的动力平衡与演变趋势是河口治理与调控的关键, 亦是保障粤港澳大湾区水安全的核心。对于珠江三角洲这一特殊“网-湾”结构的径潮相互作用的研究表明, 受大规模高强度人类活动干预(如水库建设、口门围垦、无序采砂、航道疏浚等)影响, 河口的自适应调整功能及原有均衡态的正常维持均受到不同程度的干扰, 甚至导致河口的“动力-沉积-地貌”系统的格局及演变模式发生异变(吴超羽, 2018)。位于我国粤港澳大湾区国家战略核心经济圈的珠江三角洲是全球受人类活动改造强度最大的区域之一。自20世纪80年代以来, 珠江三角洲河网地形变化显著改变河网的径潮动力格局(Zhang et al, 2015), 由于河床的不均匀下切导致不同河段的过水能力发生异变, 河网区上游分汊节点的分流分沙比均发生显著变化。1993年后, 西江通过思贤滘水道流入北江河网的分流比增加约8.8%, 造成汇入河网东四口门进入伶仃洋的分流比增加约7.7% (Luo et al, 2007)。人类活动干预后, 西江干流磨刀门水道的潮波传播过程与上下游动力边界(即流量和口门潮差)的关系发生异变, 针对水位异变的成因机制, 采用双因子回归模型、数据驱动模型等方法对水位进行分解均取得丰硕成果(杨昊等, 2020; 张先毅等, 2020; 李博等, 2022; 马玉婷等, 2022)。对于伶仃洋河口湾, 由于航道疏浚和土地围垦等原因, 潮波振幅和传播速度均有增大趋势(谢梅芳等, 2021; Zhang et al, 2021a, 2021b)。而河网区横向汊道起沟通与连结作用, 使整个“网-湾”系统在径潮动力耦合作用下趋于动态平衡。采用余水位沿河道方向的一阶(即余水位梯度)和二阶(即余水位曲率)导数研究珠江河网横向汊道体系水面线演变, 结果表明, 受关键节点分流比异变影响, 位于珠江河网上游的典型横向汊道体系“东平水道”水面线由下凹转为上凸, “容桂-凫洲水道”中上游水面线由下凹转为上凸, 中下游则下凹程度增大(王博芝等, 2021, 2022)。因此, 该区域的两条横向汊道作为维系珠江三角洲“网-湾”独特结构稳定的特殊而关键的地貌单元, 探讨其泄洪纳潮、潮能耗散、径潮动力耦合与转换等动力功能, 以及动力功能的自适应调整过程及其稳态机制是河口地貌动力研究亟需解决的重要基础和前沿科学问题, 对河网的泄洪、供水和航运策略的制定和调整均有重要影响。综上所述, 对于横向汊道径潮动力时空演变等科学问题的研究已经取得不少成果, 但关于横向汊道水位变化的影响因子辨识及其对强人类活动的响应仍是有待进一步深入探讨的重要科学问题。
1 研究区域概况本文的研究区域如图 1所示, 主要聚焦珠江河网两条典型的横向汊道体系: (1) “南沙-南华”河段(简称“容桂-凫洲水道”体系, 即自西向东分别由容桂水道、桂州水道、洪奇门水道、上横沥水道、下横沥水道、蕉门水道、凫洲水道组成的体系); (2) “黄埔-紫洞”河段(简称“潭洲-前航道”体系, 即自西向东分别由潭洲水道、平洲水道、后航道、前航道组成的体系)。珠江河网是珠江干流入海河段的特殊形态, 经多次分汊形成复杂的网状结构, 为典型的河网型水道。该类型水道由河间地分隔, 具有比降较小、中等弯曲、相互连通的特点, 是几个单一河道连通组成稳定的多河道体系。其中, “容桂-凫洲水道”体系和“潭洲-前航道”体系河段分别长约61和62 km。根据1960~2016年珠江河网水文控制站, 即马口和三水站的月均流量统计数据, 两站多年平均流量之和为8 616 m3/s, 最大月均流量达21 880 m3/s, 最小月均流量为3 988 m3/s, 具有明显的季节性差异。在洪季常出现洪潮相叠、水位涨势迅猛现象, 而枯季常出现咸潮上溯、航道淤积现象(易小兵等, 2008)。潮汐为不规则半日潮, 口门南沙站1960~2016年多年年均潮差约为1.3 m, 属弱潮河口。“容桂-凫洲水道”体系中, 容桂水道受天河、南华二级分流节点影响, 为径流主导区域; 桂州水道、上横沥水道、下横沥水道为洪潮区, 其上下游边界分别约为枯、洪季的潮区界; 凫洲水道主要受潮汐动力控制(何为, 2012)。“潭洲-前航道”体系中, “澜石-紫洞”河段为北江河网一级汊道, 同时受到径流、潮汐动力的双重影响; “黄埔-澜石”河段主要受潮汐动力影响, 水道狭窄蜿蜒, 深切发育(王博芝等, 2021)。
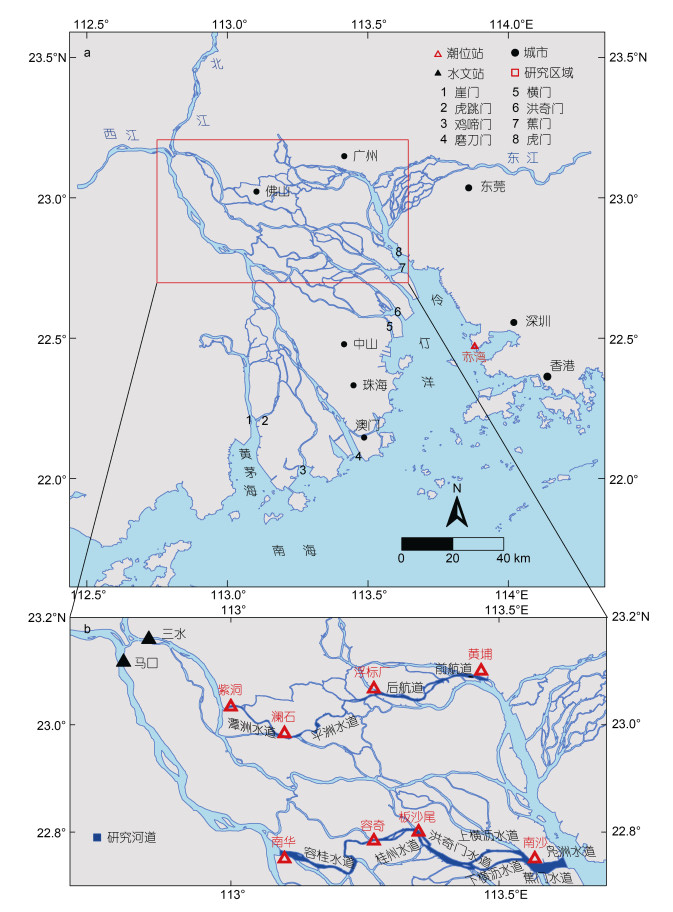 |
| 图 1 珠江河网(a)及所用潮位站和水文站位置(b) Fig. 1 The Zhujiang (Pearl) River Channel Networks (a) and tidal observational stations and hydrological gauge stations (b) |
本文所用数据取自《广东省水文年鉴》第八卷和广东省水文局, 潮位原始数据高程为冻结基面, 已统一校准至珠江基面。用于趋势分析和突变点检验的数据包括珠江河网“容桂-凫洲水道”体系4个潮位站(南沙、板沙尾、容奇、南华站)和“潭洲-前航道”体系沿程4个潮位站(黄埔、浮标厂、澜石、紫洞站) 1966~ 2016年的实测月均水位数据。用于流量驱动下潮汐调和分析的数据包括上述8个潮位站同时段的实测逐日高、低潮位数据和相应时段马口、三水水文站实测日均流量数据。采用分段三次Hermite多项式插值方法对上述高、低潮位序列和逐日流量进行插值, 获得逐时的潮位、流量数据和对应时间序列。另外, 采用伶仃洋河口湾东岸赤湾潮位站的日均水位指示海平面变化。
2.2 径潮动力特征参数的计算方法径潮动力的阶段性演变可通过水位梯度(S)来表述。基于水位(Z), 水位梯度的计算公式为
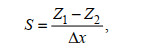 (1)
(1)式中, Z1、Z2分别为上、下游站点的水位, Δx为潮位站之间的距离。
2.3 距平曲线方法本文引入距平曲线方法来衡量年均水位的阶段性演变特征。对研究时段内的年均水位梯度进行距平, 可得距平序列, 即:
 (2)
(2)式中, si为第i年的距平值, Si为第i年的年均水位梯度, S为研究时段内年均水位梯度的均值。为消除量纲影响, 年均水位梯度作标准化处理, 即:
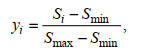 (3)
(3)式中, Smin和Smax分别为年均水位梯度的最小值和最大值, y为标准化的年均水位梯度值, 数值均在0~1之间。
2.4 R_TIDE数据驱动模型本文采用流量驱动下径潮耦合的数据驱动模型(river-driven tide harmonic analysis, R_TIDE)对逐时潮位数据进行调和分析(欧素英等, 2017; 李博等, 2022), 模型可输出重构的逐时水位、特定分潮的振幅和迟角等。在径流动力占主导的河口, 潮波上溯的非线性变化主要由上游径流动力驱动。由于传统的潮汐调和分析模型不具备分离径潮信号的功能, 因此其对受径流动力季节性变化影响强烈的河口区潮波特征的分析和预报误差较大。R_TIDE模型基于Matte等(2013, 2014)提出的非平稳调和分析(nonstationary tidal harmonic analysis, NS_TIDE)思路, 但仅由上游流量进行驱动, 而非上游流量和下游潮差。该模型假设河口任意位置的潮波振幅和迟角主要受上游流量的非线性调制影响, 在此基础上, 进一步假定分析时段河口地形边界不变, 将信号分成由流量Q引起的水位变化和潮流引起的水位变化, 基于信号分离的结果, 定量辨识感潮河段的径潮动力相互作用。
不考虑流量调制影响时, 对于月球和太阳引起的周期性潮汐现象可看作许多假想天体引起的潮汐简谐波动的总和(Pawlowicz et al, 2002)。潮位可表达成以下多个余弦函数的叠加形式:
 (4)
(4)式中, z(t)为站点的实测潮位; t为时间; z0为平均海面高度; N为分潮个数; fi为分潮振幅的订正因子, 为时间的函数, 常取一年的中值; Hi为分潮平均振幅; σi为分潮角频率, 为一定值; Vi为分潮初相角; ui为天文相角的交角订正角, gi为由于河床摩擦、水体惯性等引起的迟角。其中, Hi和gi合称为分潮调和常数。经典的潮汐调和分析可根据逐时潮位序列长度, 选择所有分潮或多个主要分潮, 采用最小二乘法求解各分潮的调和常数, 并以此预报任意时刻的潮水位(Pawlowicz et al, 2002), 因此, 式(4)可表达为
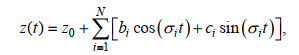 (5)
(5)式中, bi和ci为待定参数。
基于上述分析时段河口地形边界不变的假定, 采用R_TIDE数据驱动模型可率定出模型所需参数以辨识研究区域内径潮相互作用过程及机制, 因此, 基于一维圣维南方程组可得河口三角洲内任意位置x的潮波振幅变化(Kukulka et al, 2003):
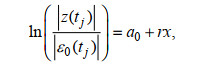 (6)
(6)式中, j=1, 2, 3, …, m, m为逐时序列的数据个数, r为衰减系数, ε0(tj)为河口口门位置x=0处的潮波振幅, a0为常数。衰减系数r随潮波传播速度、底床高程、流量和河道摩擦系数等变化(Jay et al, 1997)。采用曼宁公式计算摩擦系数, 由于摩擦系数与潮波传播速度均为底床高程的函数, 则衰减系数r可简写为底床高程h(tj)和流量Q(tj)的函数, 如式(7)所示:
 (7)
(7)或以式(8)的形式表达:
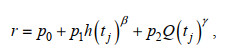 (8)
(8)式中, h(tj)和Q(tj)表示随时间变化的水深和流量(隐含有位置x的信息), p0、p1、p2、β、γ均为待定参数。与Matte等(2013, 2014)提出的NS_TIDE模型的不同的是, 式(8)未考虑外海潮汐边界的驱动影响。假定河道底床高程恒定, 则式(7)中底床高程项可归到常数项, 衰减系数r可简写为
 (9)
(9)即河口潮汐受流量驱动呈现非线性变化。结合式(5)、式(6)、式(9)可得流量影响下任意位置x的潮位变化:
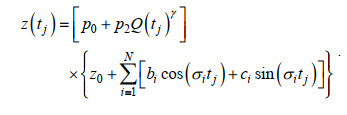 (10)
(10)通过粒子群优化算法(Kennedy et al, 1995)或求解带约束的非线性多变量方程组来确定式(10)的待定系数γ。由于不同分潮对流量的敏感程度存在差异(Cai et al, 2012; Guo et al, 2015), 如在流量影响下, 半日分潮的衰减效应大于全日分潮。因此, 采用不同的待定系数描述流量对各分潮族的调制影响, 则式(10)可表示为
 (11)
(11)将式(10)右边第一项整体与第二项内各子项相乘, 即可对应式(11)右边两项。为方便表示, 将两常数的乘积定义为一个新的变量(如下式中的d0、d1、v0, i、v1, i、r0, i、r1, i), 即可得以下两个式子:
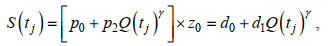 (12)
(12)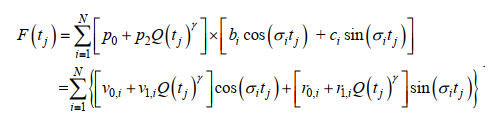 (13)
(13)式(11)即为流量驱动下的R_TIDE模型, S(tj)为底床高程、海平面、流量等变化引起的平均水面变化, 称为余水位项; F(tj)为潮流引起的水位变化, 称为潮流项。通过粒子群优化算法或求解带约束的非线性多变量方程组来确定模型的待定参数d0、d1、v0、v1、r0、r1。由于横向汊道体系上游受到径流动力强, 潮波传播过程中的非线性作用明显, 流量较大时, 三角洲上段由径流动力主导, 无潮汐波动。因此, 在R_TIDE模型中引入临界流量QC, 当连续两天潮差趋于某个值(如0.001 m)时所对应的最小流量即为临界流量, 当流量大于QC时不存在潮汐信号。
假设在河口三角洲任意位置, 时间间隔为Δt的观测潮位为y(tj)(j=1, 2, 3, …, m), 根据实测资料序列长度mΔt、分潮频率差和Rayleigh准则判据Δσ=max [(mΔt)–1, σi-σj], 选择用于调和分析的分潮, 将参数tj、σj、Q(tj)代入式(10), 并使模型计算的重构水位z(tj)和实测水位y(tj)的误差平方和ε2达到最小, 即:
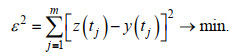 (14)
(14)选择对应资料长度的全日分潮、半日分潮等分潮族, 对实测水位进行回归拟合, 回归模型效果以均方根误差ERMS和相关系数R2描述, 表达式见式(15)~(16)。
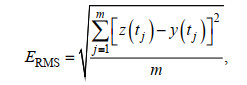 (15)
(15)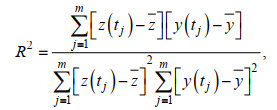 (16)
(16)式中,z和y分别表示实测水位和模拟水位时间序列的平均值。
2.5 日均水位影响因子的定量辨识方法日均水位的阶段性演变受流量、地形、海平面等多因素及其耦合效应的影响, 对日均水位受到某单一因素影响程度的定量辨识可采用R_TIDE数据驱动模型来实现。通过距平曲线方法对珠江河网横向汊道体系动力格局长周期时空演变过程进行辨识, 可划分出平衡期、异变期、调整期三个阶段(见章节3.1)。将平衡期(此时河口未出现异变)日均水位的实测值记为Zobs, pre, 调整期(此时河口已发生异变且趋于稳定)日均水位的实测值记为Zobs, post, 基于R_TIDE数据模型对平衡期逐时流量和水位实测值率定出的参数重构出的逐时水位记为Zsim, pre, 采用平衡期率定参数并以调整期日均流量进行驱动得到的调整期计算值记为Zsim, post。
为定量辨识不同因子对珠江河网横向汊道体系日均水位的影响, 引入总变化值(∆ZTOT)、上游流量驱动下的变化值(∆ZDIS)以及地形和海平面共同驱动下的变化值(∆ZGEO_MSL)。总变化值为调整期的实测值减去平衡期的实测值, 反映两个阶段日均水位的实际变化量; 上游流量驱动下的变化值∆ZDIS为调整期计算值减去平衡期的实测值, 反映上游动力边界的影响, 即上游流量, 其变化主要受控于上游水库调蓄; 地形和海平面共同驱动下的变化值∆ZGEO_MSL为调整期的实测值减去调整期的计算值, 反映除流量影响外, 地形边界和外海边界的影响, 即采砂、围垦以及水库建设等活动导致地形的变化及海平面变化的影响。基于上述假设和定义, 日均水位阶段性演变的影响因子计算方法为(杨昊等, 2020):
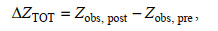 (17)
(17)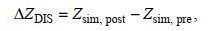 (18)
(18) (19)
(19)模型的误差δ定义为平衡期的计算水位与实测水位之差, 即:
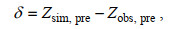 (20)
(20)因此, 日均水位的阶段性变化值主要由流量驱动、地形和海平面共同影响以及模型误差三部分组成, 结合式(17)~式(20), 可得
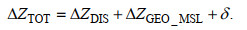 (21)
(21)为定量辨识R_TIDE模型中余水位项S(t)和潮流项F(t)对水位的贡献率, 引入方差贡献率(variance contribution rate, VCR)分析水位序列的主导因子演变, 其方差贡献率分别为
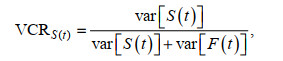 (22)
(22)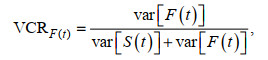 (23)
(23)式中, 符号var表示计算时间序列的方差, VCRS(t)和VCRF(t)分别表示模型中余水位项S(t)和潮流项F(t)的水位方差贡献率。
3 结果分析 3.1 径潮动力的阶段性演变以珠江河网“容桂-凫洲水道”体系和“潭洲-前航道”体系的年均水位梯度为切入点, 通过距平曲线方法探究该体系径潮动力格局的阶段性异变过程及特征。根据图 2所示的距平曲线可知, 在1988年以前, 曲线位于代表距平值为0的实线上方, 表明此阶段为正距平; 1989~1998年, 该阶段“容桂-凫洲水道”和“潭洲-前航道”体系的距平曲线在0附近波动, 无量纲年均水位梯度方差分别仅为0.02和0.04, 正负距平交替; 1999年以后, 距平值均小于0 (即负距平)。根据距平曲线划分出的阶段, 1966~1988年, “容桂-凫洲水道”体系和“潭洲-前航道”体系的年均水位梯度均值分别为1.69×10–5和1.58×10–5; 1999~2016年均值分别降为8.54×10–6和9.96×10–6, 两阶段相比分别减小49%和58%。因此, 可将珠江河网横向汊道体系径潮动力格局的演变分为三个阶段: 1988年前为自然演变和人类活动共同作用的阶段, 但此阶段人类活动尚未对横向汊道体系的径潮动力格局产生明显影响, 河网以自然演变为主, 称为“平衡期”; 1998年后, 河道中下游采砂活动基本已停止, 滩涂围垦面积锐减, 河网在人类活动影响下已发生径潮动力格局稳态转换, 两条横向汊道水位梯度距平曲线的变化基本重合, 表明河网横向汊道体系的径潮动力变化趋于同步, 动力结构趋于稳定, 为强人类活动干预后河网的自适应调整阶段, 称为“调整期”; 1988~1998年为人类活动影响最强烈的时期, 河网从自然演变为主的平衡态向强人类活动干预后的平衡态转变, 为两个平衡态的过渡阶段, 称为“异变期”(张先毅等, 2020)。
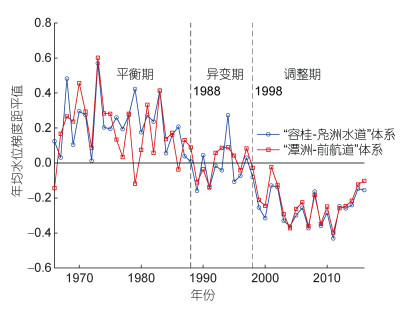 |
| 图 2 珠江河网横向汊道体系年均水位梯度距平曲线及阶段性划分 Fig. 2 Accumulated anomaly curve of yearly averaged water level slope in transverse channel system in the Zhujiang (Pearl) River Channel Networks |
水位梯度的变化主要是水位的时空不均匀性引起。根据距平曲线划分的横向汊道体系径潮格局的阶段性演变, 平衡期和调整期的多年日均水位过程线如图 3所示。图 3a~3d为“容桂-凫洲水道”体系沿程4个站点的日均水位变化。从年内分布来看, 洪季阶段水位高, 枯季水位低, 洪峰从平衡期的7月前移至调整期的6月; 从阶段性差异来看, 除南沙站的水位有所抬升(约0.10 m)外, 板沙尾、容奇、南华3个站点的水位均有不同程度的下降, 且具有从口门向上游累积的效应, 水位分别下降约0.09、0.10、0.41 m, 仅冬季水位略有抬升, 而夏季(6月份除外)和秋季水位大幅下降。图 3e~3f为“潭洲-前航道”体系沿程4个站点的日均水位变化。类似地, 沿程站点的水位在洪季阶段高, 枯季阶段低。从阶段性差异来看, 除黄埔站水位抬升0.07 m外, 其余3个站点的水位均有不同程度的下降, 且同样具有从口门向上游累积的效应, 水位分别下降约0.06、0.16、0.42 m。浮标厂站全年的水位均有小幅度下降, 夏季较明显; 澜石、紫洞站的水位变化则表现为冬季略有抬升, 夏季(6月份除外)、秋季大幅下降。
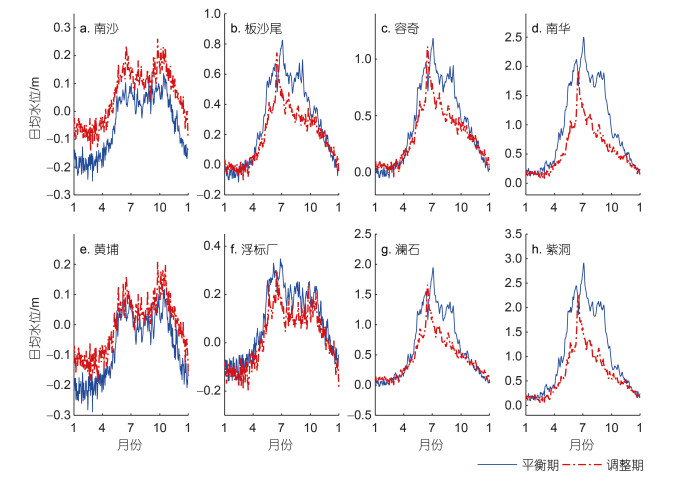 |
| 图 3 强人类活动前后珠江河网横向汊道体系日均水位过程线 Fig. 3 Daily averaged water level in transverse channel system in the Zhujiang (Pearl) River Channel Networks in pre- and post-human period |
为验证R_TIDE数据驱动模型的效果, 采用平衡期前2/3的数据(1966~1982年)用于率定, 并应用于后1/3的数据(1983~1988年)作为验证。由于“容桂-凫洲水道”体系是连接西北江中下游河网的重要通道, 因此, 其输入的流量边界为马口与三水流量之和; “潭洲-前航道”体系位于北江干流且其上边界即为三水水文站, 因此, 其输入的流量边界为三水流量。绘制实测水位与模型重构水位的散点图, 如图 4所示, 其中黑色虚线表示实测与重构水位相等的等值线。当流量大于临界流量QC时潮波基本消失(仅南华、澜石、紫洞的潮波信号受流量影响较大, 其QC分别为29 800、7 600和3 400 m3/s), 率定验证过程中流量超过QC时所对应的潮波信号为虚假信号, 结果分析部分已剔除这部分信息。
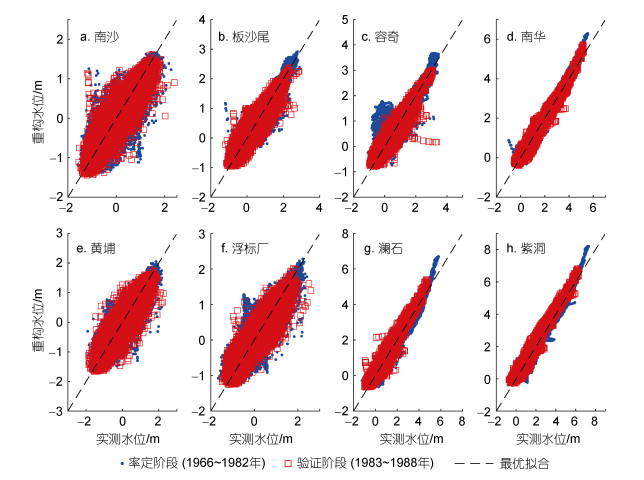 |
| 图 4 R_TIDE数据驱动模型率定验证效果 Fig. 4 Performance of R_TIDE data-driven model verification |
为评价R_TIDE数据驱动模型对径潮信号分离的效果, 采用公式(15)~(16)计算实测与重构水位的ERMS和R2并统计于表 1。由表 1可见, 越往下游, ERMS值越大, 表明模型对潮流优势区域水位的重构效果略低于上游区域, 但其R2均大于0.83, 模型计算结果与实测值吻合良好。验证阶段的ERMS比率定阶段普遍增大, R2则减小, 表明验证阶段横向汊道体系的日均水位已经受到少量人类活动的干扰, 但是其R2均大于0.82。因此, R_TIDE模型重构的水位序列可用于后续的分析预报。
| 站点 | ERMS/m | R2 | |||
| 率定阶段 | 验证阶段 | 率定阶段 | 验证阶段 | ||
| 南沙 | 0.25 | 0.26 | 0.83 | 0.82 | |
| 板沙尾 | 0.22 | 0.23 | 0.90 | 0.87 | |
| 容奇 | 0.22 | 0.22 | 0.92 | 0.89 | |
| 南华 | 0.17 | 0.18 | 0.99 | 0.97 | |
| 黄埔 | 0.27 | 0.26 | 0.85 | 0.85 | |
| 浮标厂 | 0.25 | 0.23 | 0.83 | 0.83 | |
| 澜石 | 0.22 | 0.22 | 0.97 | 0.95 | |
| 紫洞 | 0.19 | 0.22 | 0.99 | 0.98 | |
日均水位作为指示径潮动力变化的重要参数, 其阶段性变化受到流量、地形、海平面等多种因素及其耦合作用影响。采用公式(17)~(20)可定量辨识珠江河网横向汊道日均水位阶段性异变的影响因子。图 5为本文所用8个站点的ΔZDIS (上游流量驱动下的变化值)和ΔZGEO_MSL (地形和海平面共同驱动下的变化值)的日均过程线, 它们的季节差异和年均变化统计于表 2。
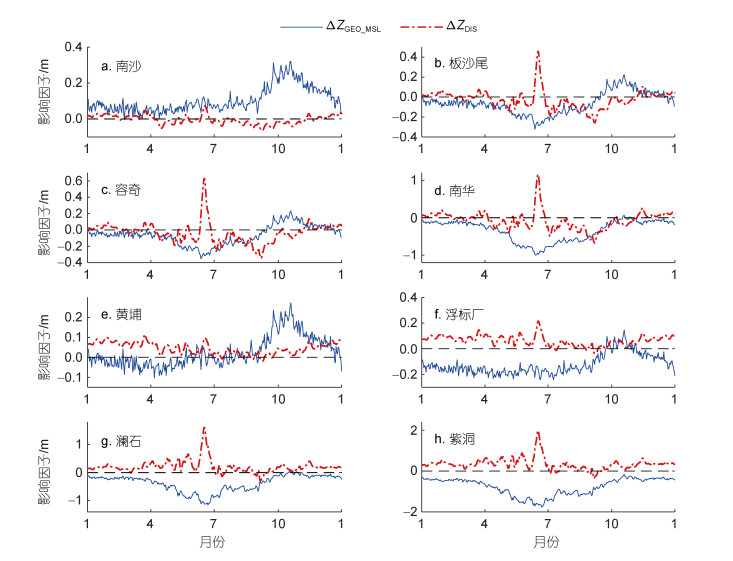 |
| 图 5 珠江河网横向汊道体系ΔZDIS和ΔZGEO_MSL的日均过程线 Fig. 5 Daily averaged ΔZDIS and ΔZGEO_MSL in transverse channel system in the Zhujiang (Pearl) River Channel Networks 注: ΔZDIS表示上游流量驱动下的水位变化值, ΔZGEO_MSL表示地形和海平面共同驱动下的水位变化值 |
| 站点 | 季节 | 参数 | |
| ΔZDIS/m | ΔZGEO_MSL/m | ||
| 南沙 | 春 | 0.00 | 0.05 |
| 夏 | 0.01 | 0.08 | |
| 秋 | −0.02 | 0.20 | |
| 冬 | 0.02 | 0.08 | |
| 年均 | 0.00 | 0.11 | |
| 板沙尾 | 春 | −0.03 | −0.11 |
| 夏 | −0.04 | −0.17 | |
| 秋 | −0.05 | 0.07 | |
| 冬 | 0.02 | −0.03 | |
| 年均 | −0.03 | −0.06 | |
| 容奇 | 春 | −0.04 | −0.10 |
| 夏 | −0.06 | −0.19 | |
| 秋 | −0.07 | 0.08 | |
| 冬 | 0.03 | −0.03 | |
| 年均 | −0.03 | −0.06 | |
| 南华 | 春 | −0.07 | −0.38 |
| 夏 | −0.12 | −0.71 | |
| 秋 | −0.15 | −0.16 | |
| 冬 | 0.07 | −0.12 | |
| 年均 | −0.07 | −0.34 | |
| 黄埔 | 春 | 0.05 | −0.04 |
| 夏 | 0.02 | 0.00 | |
| 秋 | 0.03 | 0.13 | |
| 冬 | 0.07 | 0.00 | |
| 年均 | 0.05 | 0.02 | |
| 浮标厂 | 春 | 0.08 | −0.18 |
| 夏 | 0.05 | −0.17 | |
| 秋 | 0.04 | −0.01 | |
| 冬 | 0.09 | −0.13 | |
| 年均 | 0.06 | −0.12 | |
| 澜石 | 春 | 0.28 | −0.46 |
| 夏 | 0.26 | −0.72 | |
| 秋 | 0.13 | −0.14 | |
| 冬 | 0.18 | −0.17 | |
| 年均 | 0.21 | −0.37 | |
| 紫洞 | 春 | 0.44 | −0.90 |
| 夏 | 0.36 | −1.26 | |
| 秋 | 0.22 | −0.50 | |
| 冬 | 0.35 | −0.41 | |
| 年均 | 0.34 | −0.77 | |
| 注: ΔZDIS表示上游流量驱动下的水位变化值, ΔZGEO_MSL表示地形和海平面共同驱动下的水位变化值 | |||
从年内分布来看, 南沙站由流量驱动引起的水位变化ΔZDIS基本在0附近波动, 表明其水位受上游流量的影响较小; 板沙尾、容奇、南华站的ΔZDIS在冬季为正值, 其余三季为负值, 主要反映水库的调蓄作用(即洪季蓄水、枯季放水)。值得注意的是, 在6月份ΔZDIS有明显的抬升, 其量值甚至大于最小值的绝对值, 且越往上游, 其最大值越大(“南沙-南华”河段ΔZDIS最大值分别为0.07、0.46、0.64、1.16 m), 反映水库调蓄引起的流量年内分配变化(即调整期阶段流量最大值从7月前移至6月), 虽然夏季部分时段的ΔZDIS为正值, 但是在“容桂-凫洲水道”体系, 该值仍小于0。在“潭洲-前航道”体系, 由于在20世纪90年代后西北江的流量分配发生显著变化, 流入三水站的流量增多(调整期平均增大435 m3/s), 因此, ΔZDIS在“潭洲-前航道”体系基本为正值, 其中春、冬两季较小, 夏季较大, 该现象出现同样是由于受到洪峰移动的影响, 且其受到的影响程度大于“南沙-南华”河段, “黄埔-紫洞”河段ΔZDIS最大值分别为0.12、0.22、1.62、2.00 m。受到流量年内重新分配影响, 夏季部分时段的ΔZDIS为负值且ΔZDIS小于春季, 澜石、紫洞的春季和夏季之差分别为0.02、0.08 m (表 2)。
另一方面, 日均水位变化受到地形和海平面共同驱动的影响。由地形和海平面共同驱动引起的水位变化ΔZGEO_MSL在南沙站基本为正值, 表明其受到口门围垦以及相对海平面上升的影响, 其中ΔZGEO_MSL在秋季量值较大, 其他几个站点也有类似现象, 反映海平面的重要影响(即海平面高程在秋季最大, 为0.14 m); 板沙尾、容奇、南华三个站点ΔZGEO_MSL在其他三季均为负值, 表明航道疏浚、人为采砂等强人类活动影响导致的河床下切引起的水位下降效应明显大于海平面上升的影响, 特别是在流量较大的夏季, 水位下降尤为明显。在“潭洲-前航道”体系, 所有站点的ΔZGEO_MSL均为负值, 表明在北江干流河道进行的疏浚、采砂等人类活动导致底床高程下降, 水位为适应地形变化也有相应的下降。位于横向汊道体系上游的南华、紫洞站的ΔZGEO_MSL在夏季最小, 冬季最大, 表明地形下切的影响在大流量条件下更明显, 该现象出现在径流控制河段。
3.5 日均水位梯度的变化图 6为珠江河网横向汊道体系日均水位梯度的年内分布, 其中图 6a为“南沙-南华”河段日均水位梯度的变化, 图 6b~6d为相邻站点间日均水位梯度的变化, 灰色阴影部分表示地形叠加海平面的影响, 蓝色阴影部分表示流量驱动的影响。由于洪峰前移, 导致日均水位梯度的最大值从7月前移至6月。各河段日均水位的变化主要受地形下切的影响, 由于河网中上游地区底床高程降低, 而下边界海平面上升, 水面线为适应地形变化导致水位梯度变缓; 另一方面, 由于水库调蓄的影响, 冬季的ΔSDIS为正, 表明流量增加导致水位梯度变陡, 其余三季的ΔSDIS为负。值得注意的是, “板沙尾-容奇”河段的水位梯度变化基本不受地形影响(即蓝色实线与红色虚线几乎重合), 而主要受到流量变化影响, 但是其变化规律与其他河段基本一致。其中图 6e为“潭洲-前航道”体系中“黄埔-紫洞”河段日均水位梯度的变化, 图 6f~6h为相邻站点间日均水位梯度的变化。与“容桂-凫洲水道”体系不同, “潭洲-前航道”体系的水位梯度全年均受流量增加的影响而变陡, 亦受到地形下切的影响而变缓, 两种效应相互抵消, 最终使“潭洲-前航道”体系的水位梯度变缓。
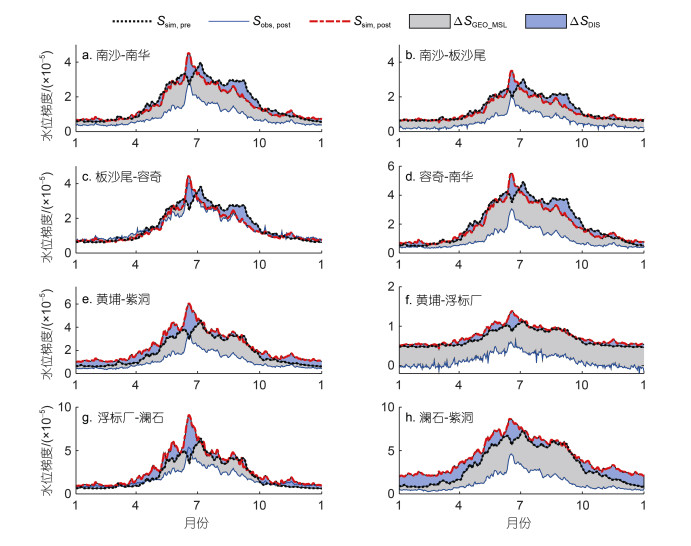 |
| 图 6 强人类活动前后珠江河网“容桂-凫洲水道”和“潭洲-前航道”体系日均水位梯度的年内分布 Fig. 6 Daily averaged water level slope of "Ronggui-Fuzhou Channel" and "Tanzhou-Front Channel" system in Pre- and post-human period in different sections 注: Ssim, pre表示采用平衡期率定参数并以平衡期日均流量进行驱动得到的平衡期水位梯度计算值, Sobs, post表示调整期阶段水位梯度的实测值, Ssim, post表示采用平衡期率定参数并以调整期日均流量进行驱动得到的调整期水位梯度计算值, ΔSDIS表示上游流量驱动下的水位梯度变化值, ΔSGEO_MSL表示地形和海平面共同驱动下的水位梯度变化值 |
表 3统计了日均水位梯度异变影响因子的季节和年均差异。在“容桂-凫洲水道”体系, ΔSTOT的变化以夏季最大, 冬季最小(“板沙尾-容奇”河段除外, 为春季最小, 约为3.79×10−7), 且差异呈现先减小后增大的趋势(“南沙-板沙尾”河段夏、冬两季差异为7.80×10−6, “容奇-南华”河段减小为6.51×10−6, “容奇-南华”河段则增大为1.82×10−5)。在“潭洲-前航道”体系的规律类似, 但是越往上游, 季节差异越大(“黄埔-浮标厂”河段夏、冬两季差异为9.84×10−7, “澜石-紫洞”河段则为2.82×10−5), 反映了水位梯度变化的空间不均匀性。ΔSDIS的变化揭示了水库调蓄的作用, 在“容桂-凫洲水道”体系, 冬季的ΔSDIS为正值, 表明冬季流量增加使得水位梯度变陡, 其余季节由于流量减小, 水位梯度相应变缓; 在“潭洲-前航道”体系, ΔSDIS为正值, 表明北江流量增大后, “潭洲-前航道”体系的水位梯度变陡。ΔSGEO_MSL的变化与ΔSTOT的变化相同, 表明水位梯度主要受到地形下切的影响, 但是值得注意的是, 在“容桂-凫洲水道”体系中, 除冬季和“板沙尾-容奇”河段的春季, ΔSGEO_MSL的变化与ΔSDIS符号相同, 表明地形变化与流量变化均导致水位梯度变缓, 二者的效应相同; 在“潭洲-前航道”体系, 除“浮标厂-澜石”河段的冬季, ΔSGEO_MSL的变化与ΔSDIS符号相反, 表明一方面地形下切导致水位梯度变缓, 另一方面流量增加又导致水位梯度变陡, 二者的效应相互抵消, 但是综合而言, 流量增大的影响程度小于地形下切, 因此, “潭洲-前航道”体系的水位梯度在调整期变缓。
| 区域 | 季节 | 参数 | ||
| ΔSTOT | ΔSDIS | ΔSGEO_MSL | ||
| 南沙-南华 | 春 | −8.18×10−6 | −1.14×10−6 | −7.08×10−6 |
| 夏 | −1.47×10−5 | −1.80×10−6 | −1.29×10−5 | |
| 秋 | −7.84×10−6 | −2.08×10−6 | −5.90×10−6 | |
| 冬 | −2.56×10−6 | 9.08×10−7 | −3.28×10−6 | |
| 年均 | −8.34×10−6 | −1.03×10−6 | −7.31×10−6 | |
| 南沙-板沙尾 | 春 | −7.43×10−6 | −9.82×10−7 | −6.32×10−6 |
| 夏 | −1.13×10−5 | −1.41×10−6 | −1.02×10−5 | |
| 秋 | −7.37×10−6 | −1.23×10−6 | −5.15×10−6 | |
| 冬 | −3.53×10−6 | 2.78×10−7 | −4.70×10−6 | |
| 年均 | −7.43×10−6 | −8.36×10−7 | −6.59×10−6 | |
| 板沙尾-容奇 | 春 | 3.79×10−7 | −1.14×10−6 | 3.74×10−7 |
| 夏 | −4.73×10−6 | −1.79×10−6 | −2.16×10−6 | |
| 秋 | −2.10×10−6 | −1.79×10−6 | 3.36×10−7 | |
| 冬 | 1.78×10−6 | 6.97×10−7 | 8.09×10−7 | |
| 年均 | −1.17×10−6 | −1.01×10−6 | −1.65×10−7 | |
| 容奇-南华 | 春 | −1.18×10−5 | −1.30×10−6 | −1.03×10−5 |
| 夏 | −2.13×10−5 | −2.17×10−6 | −1.92×10−5 | |
| 秋 | −1.02×10−5 | −2.98×10−6 | −8.73×10−6 | |
| 冬 | −3.11×10−6 | 1.57×10−6 | −3.33×10−6 | |
| 年均 | −1.16×10−5 | −1.22×10−6 | −1.04×10−5 | |
| 黄埔-紫洞 | 春 | −7.74×10−6 | 6.26×10−6 | −1.38×10−5 |
| 夏 | −1.51×10−5 | 5.37×10−6 | −2.03×10−5 | |
| 秋 | −6.88×10−6 | 3.06×10−6 | −1.01×10−5 | |
| 冬 | −2.01×10−6 | 4.40×10−6 | −6.62×10−6 | |
| 年均 | −7.95×10−6 | 4.78×10−6 | −1.27×10−5 | |
| 黄埔-浮标厂 | 春 | −5.60×10−6 | 1.04×10−6 | −6.03×10−6 |
| 夏 | −5.92×10−6 | 9.31×10−7 | −7.11×10−6 | |
| 秋 | −5.35×10−6 | 5.41×10−7 | −6.03×10−6 | |
| 冬 | −4.94×10−6 | 5.12×10−7 | −5.68×10−6 | |
| 年均 | −5.46×10−6 | 7.57×10−7 | −6.21×10−6 | |
| 浮标厂-澜石 | 春 | −3.03×10−6 | 7.85×10−6 | −1.12×10−5 |
| 夏 | −1.37×10−5 | 8.40×10−6 | −2.18×10−5 | |
| 秋 | −2.50×10−6 | 3.32×10−6 | −5.00×10−6 | |
| 冬 | 2.84×10−6 | 3.62×10−6 | −1.54×10−6 | |
| 年均 | −4.13×10−6 | 5.81×10−6 | −9.94×10−6 | |
| 澜石-紫洞 | 春 | −2.06×10−5 | 1.26×10−5 | −3.27×10−5 |
| 夏 | −3.42×10−5 | 7.56×10−6 | −4.09×10−5 | |
| 秋 | −1.80×10−5 | 7.11×10−6 | −2.73×10−5 | |
| 冬 | −6.02×10−6 | 1.29×10−5 | −1.80×10−5 | |
| 年均 | −1.97×10−5 | 1.00×10−5 | −2.98×10−5 | |
| 注: ΔSTOT表示调整期和平衡期之间的水位梯度变化值, ΔSDIS表示上游流量驱动下的水位梯度变化值, ΔSGEO_MSL表示地形和海平面共同驱动下的水位梯度变化值 | ||||
为揭示珠江河网横向汊道体系日均水位阶段性变化的原因, 分析其上下游动力边界的阶段性异变, 探究“容桂-凫洲水道”体系上游流量边界(即马口与三水流量之和)、“潭洲-前航道”体系上游流量边界(即三水流量)以及下游海平面边界(即赤湾水位)的阶段性变化, 如图 7所示。流量的阶段性变化是导致水位发生下降的重要原因之一。由图 7a可见, 马口与三水流量之和在冬季略有增大(约为585 m3/s), 在春、夏和秋三季均有明显减小(分别减小约584、971和1 194 m3/s), 因此, 正如3.2部分图 3所示, 在“容桂-凫洲水道”体系中, 各站点实测水位在秋季亦有明显下降, 其中ΔZDIS在冬季大于0, 在秋季达到最小值。由图 7b可见, 三水流量在全年均有增大(7~9月部分时段除外), 因此“潭洲-前航道”体系中各站点的ΔZDIS均大于0。由于在秋季, 三水流量在部分时段减小, 引起水位下降, 所以ΔZDIS在秋季最小, 但仍大于0; 流量在春季增加幅度最大(571 m3/s), 其次为夏季(509 m3/s), 因此, 澜石、紫洞站ΔZDIS在春季达到最大。
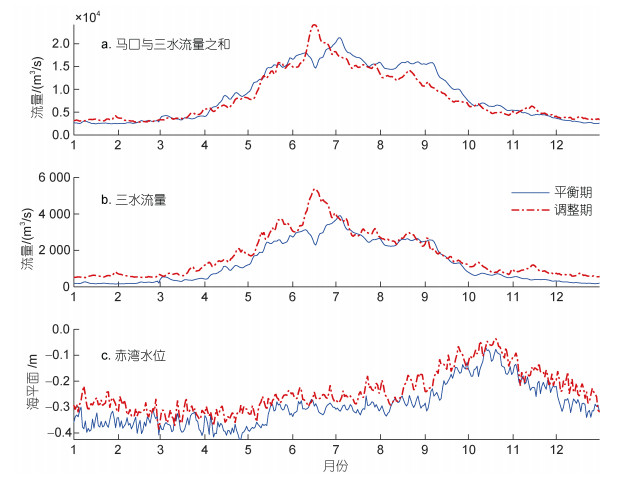 |
| 图 7 强人类活动前后珠江河网横向汊道体系上下游动力边界的变化 Fig. 7 Changes of upstream and downstream dynamic boundary conditions in transverse channel system in the Zhujiang (Pearl) River Channel Networksin pre- and post-human period |
对于下游海平面边界, 以伶仃洋东岸的赤湾验潮站日均水位作为指示变量。由图 7c可见, 红色虚线普遍位于蓝色实线上方, 表明调整期阶段, 相对海平面明显上升(上升约0.05 m)。从年内分布来看, 赤湾水位在秋季达到最大(平衡期、调整期分别为−0.18和−0.13 m), 在春季达到最小(平衡期、调整期分别为−0.36和−0.31 m), 上述现象亦导致口门两个站点(南沙、黄埔站)的ΔZTOT、ΔZDIS和ΔZGEO_MSL均为正, 表明各因子均导致水位抬升。而在“容桂-凫洲水道”体系中, 板沙尾、容奇站的ΔZGEO_MSL在秋季大于0, 表明秋季海平面上升的影响大于河床下切的影响, 导致日均水位抬升。
对于地貌边界异变的影响研究, 以围垦、采砂、疏浚导致的地形变化为切入点进行探讨。大规模的围垦易导致河道变窄, 口门潮位抬升, 影响潮能耗散。自20世纪90年代初, “容桂-凫洲水道”体系经历强烈的采砂活动和航道疏浚, 在1984~1999年间, 西北江河网区主要河道年均采砂量4.6~5.3×107 m3, 远大于其年均淤积量(黄镇国等, 2004); 1996~2006年间, 马口-天河的疏浚量超过1.27×107 m3 (刘宏霄等, 2019)。上述人类活动导致“容桂-凫洲水道”体系平均水深增加1.11 m, 水面均宽减小约34 m (郑国栋, 2005)。根据对1990~1992和2015年洪季南华、容奇、板沙尾、南沙的基本水尺断面分析, 2015年基本水位较1993年前分别下降1.18、−0.38、0.81、0.79 m, 除板沙尾横断面水位略有上升外, 其余站点的断面水位均有较明显下降(王博芝等, 2022)。对于“潭洲-前航道”体系, 受到强人类活动影响, 平均水深增加0.93 m, 水面均宽减小约72 m (王博芝等, 2021)。因此, 即便是流量略有增大, 但是为适应地形窄深化的影响, 相同流量条件下, 珠江河网横向汊道体系的水位出现相应下降。
4.2 径潮动力贡献率的变化针对横向汊道体系径潮动力及泄洪纳潮功能的演变, 基于R_TIDE模型水位的组成部分, 探究余水位项S(t) (主要代表河流动力)和潮流项F(t) (主要代表海洋动力)的时空演变特征。图 8为横向汊道体系S(t)和F(t)在夏季和冬季的方差贡献率。由图 8a和8b可知, 在夏季, “容桂-凫洲水道”口门处南沙站的S(t)贡献率在调整期阶段有所增加, 但是量值较小(仅增大1%), 表明南沙站水位变化主要由海洋动力驱动。板沙尾及其上游站点的S(t)贡献率明显下降, 其中板沙尾站水位S(t)贡献率由54%减小至38%, 表明该站点水位的主控影响因子由平衡期的径流驱动逐渐转换为调整期的潮流驱动; 容奇、南华站S(t)贡献率分别减小10%和5%。在夏季, “潭洲-前航道”横向汊道体系下游黄埔、浮标厂站的水位主要由海洋动力控制, 平衡期和调整期的F(t)方差贡献率均超过91%; 位于中上游的澜石、紫洞站的S(t)贡献率分别减小9%和4%, 表明水位对流量的响应有所减弱。综上可知, 在调整期阶段的夏季时期, 由于水库调蓄作用, 流入“容桂-凫洲水道”的流量减小, 流入“潭洲-前航道”体系的流量增加, 但由于地形下切效应, 流量的贡献率普遍减小, 表明横向汊道体系的泄洪压力相对减小, 纳潮能力相应增大。
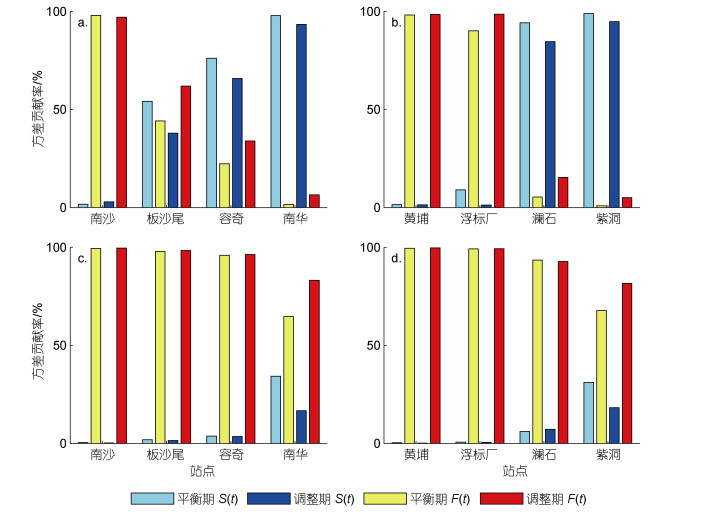 |
| 图 8 珠江河网横向汊道体系S(t)和F(t)贡献率的对比 Fig. 8 Variance contribution rates of S(t) and F(t) in transverse channel system in the Zhujiang (Pearl) River Channel Networks 注: a. 夏季, “容桂-凫洲水道”体系; b. 夏季, “潭洲-前航道”体系; c. 冬季, “容桂-凫洲水道”体系; d. 冬季, “潭洲-前航道”体系; S(t)和F(t)分别表示R_TIDE模型中的余水位项和潮流项 |
在冬季, 位于口门的南沙、黄埔站的S(t)贡献率均小于1%, 板沙尾、浮标厂的S(t)贡献率小于2%, 基本由潮动力控制。位于两条横向汊道体系中部的容奇、澜石站S(t)贡献率基本不变。上游南华、紫洞站的S(t)贡献率分别减小17%和13%, 表明虽然流量增大, 但由于潮动力增强(冬季潮差分别增大0.10、0.15 m), S(t)贡献率仍减小。因此, 与之对应的是F(t)贡献率的增加, 表明冬季纳潮能力增大, 咸潮上溯的风险有所加剧。
4.3 横向汊道体系中纵横水道的径潮动力特征对比基于上述分析可得“容桂-凫洲水道”和“潭洲-前航道”两个典型横向汊道体系的径潮动力时空演变特征, 但作为连通上述两个横向汊道体系的纵向水道, 即“容奇-紫洞”和“板沙尾-澜石”河段与横向汊道水位演变的差异性仍是有待深入探究的问题。针对单个站点的径潮动力特征分析已在章节3.4和4.2中提及, 因此, 本节以两条纵向水道的水位梯度异变影响因子为切入点, 探究复杂河网纵横水道径潮动力时空演变特征的异同。
从水位梯度异变影响因子的季节和年均差异来看(表 4), 两条横向汊道的水位梯度总变化值(ΔSTOT)均大于纵向水道(表 3和表 4), 其中, “南沙-南华”与“黄埔-紫洞”两条横向汊道ΔSTOT的年均值分别为−8.34×10−6和−7.95×10−6, 略大于“容奇-紫洞”河段(约为−6.50×10−6), 明显大于“板沙尾-澜石”河段(约为−2.12×10−6)。从季节差异来看, 该现象在夏季尤为明显(上述四个河段夏季的极差值为8.38×10−6), 冬季则相差较小(极差值为3.66×10−6), 表明在该体系中水位的横比降变化对径潮动力格局异变的响应更为明显。两条纵向水道在上游流量驱动下的水位梯度变化值ΔSDIS均为正值, 表明纵向水道的水位梯度受北江流量增大的影响, 导致水位梯度变陡, 且年均绝对值均大于两个横向汊道体系(表 3和表 4)。从季节变化来看, 不同于“南沙-南华”河段秋季ΔSDIS绝对值最大而冬季绝对值最小的现象, 其余各河段均是春季最大, 但“容奇-紫洞”河段的最小值出现在秋季, 与“澜石-紫洞”河段现象相似。两条纵向水道在地形和海平面共同驱动下的变化值ΔSGEO_MSL均为负值, 表明以河道下切为主的影响因子导致水位梯度变缓。对于上游的“容奇-紫洞”河段, 其年均值均大于两条横向汊道, 表明地形和海平面的变化对水位梯度的影响在上游的纵向水道更为明显。对于中下游的“板沙尾-澜石”河段, 虽然影响效应相同, 但是量值介于两条横向汊道之间, 接近于“浮标厂-澜石”和“板沙尾-南沙”河段ΔSGEO_MSL的平均值(约为−8.27×10−6), 由此可见, 该河段地形和海平面对水位梯度的影响介于两条横向汊道之间; 从季节变化来看, 该现象在冬季最显著, 表现为“板沙尾-澜石”河段冬季的ΔSGEO_MSL最接近于“浮标厂-澜石”和“板沙尾-南沙”河段的平均值(差值仅为5.66×10−7), 其次为秋季、春季和夏季(与“浮标厂-澜石”和“容奇-南华”河段的平均值差值为1.16×10−6)。上述结果表明, 作为沟通北江干流水道和西江二级分流节点的两条纵向水道, 其水位梯度变化的两个影响因子作用相反, 一方面受到北江流量增大的影响, 水位梯度变陡; 另一方面则受到海平面和地形变化影响而变缓。值得注意的是, 下游“板沙尾-澜石”河段的水位梯度对地形和海平面变化的响应对其上下端相连的两个横向汊道体系径潮动力格局的动态平衡起着关键作用。因此, 未来宜将河网区视为有机联系的整体, 进一步深入探讨该体系中纵横水道之间径潮动力的耦合和协同效应。
| 纵向河道 | 季节 | 参数 | ||
| ΔSTOT | ΔSDIS | ΔSGEO_MSL | ||
| 容奇-紫洞 | 春 | −6.63×10−6 | 9.54×10−6 | −1.57×10−5 |
| 夏 | −1.30×10−5 | 8.32×10−6 | −2.11×10−5 | |
| 秋 | −4.82×10−6 | 5.74×10−6 | −1.14×10−5 | |
| 冬 | −1.50×10−6 | 6.30×10−6 | −7.55×10−6 | |
| 年均 | −6.50×10−6 | 7.48×10−6 | −1.40×10−5 | |
| 板沙尾-澜石 | 春 | −1.59×10−6 | 8.30×10−6 | −9.71×10−6 |
| 夏 | −6.72×10−6 | 8.27×10−6 | −1.48×10−5 | |
| 秋 | −6.48×10−7 | 4.88×10−6 | −5.82×10−6 | |
| 冬 | 5.48×10−7 | 4.18×10−6 | −3.69×10−6 | |
| 年均 | −2.12×10−6 | 6.42×10−6 | −8.53×10−6 | |
| 注: ΔSTOT表示调整期和平衡期之间的水位梯度变化值, ΔSDIS表示上游流量驱动下的水位梯度变化值, ΔSGEO_MSL表示地形和海平面共同驱动下的水位梯度变化值 | ||||
(1) 采用R_TIDE数据驱动模型辨识横向汊道水位异变的影响因子, 日均水位的变化可分解为由流量驱动引起的变化和由地形和海平面共同驱动引起的变化。结果表明, 由流量驱动引起的水位变化(ΔZDIS)在冬季大于0, 反映流量年内分配变化引起的水位变化。在“南沙-南华”河段, 四个季节的ΔZDIS均小于0 (分别为−0.02、−0.05、−0.07、−0.15 m), 且在秋季最小, 该现象是由于洪峰前移导致。在“黄埔-紫洞”河段, 该值均大于0, 反映北江流量增大引起的水位抬升现象。由地形和海平面共同驱动引起的水位变化(ΔZGEO_MSL)除在南沙、黄埔、板沙尾和容奇站的秋季大于0外, 其余均小于0, 表明在这些站点水位主要受到围垦和海平面上升的影响; 其余站点则主要受到地形下切的影响, 水位为适应底床高程变化而下降。
(2) 与日均水位的变化类似, 可对水位梯度进行分解进一步探讨水位异变成因机制。结果表明, “南沙-南华”河段的ΔSDIS在冬季均大于0, 表明冬季流量增大导致水位梯度变陡, 其余季节(除“板沙尾-容奇”河段)均小于0。“黄埔-紫洞”河段由于北江流量增大, 其ΔSDIS均大于0; 除部分河段的春、冬两季外, ΔSGEO_MSL均小于0, 表明地形下切与海平面上升的综合影响导致水位梯度变缓, 且ΔSGEO_MSL在夏季最小, 冬季最大, 表明在径流动力强的情况下其影响强度增大。
(3) 针对横向汊道泄洪纳潮功能演变问题, 由S(t)和F(t)贡献率的分析可知, “容桂-凫洲水道”作为蕉门河口的上游, 夏季S(t)贡献率明显下降(平均为10%), 与ΔZDIS减小对应, 泄洪压力减小, 且板沙尾站的主控影响因子由平衡期的径流驱动逐渐转换为调整期的潮流驱动, 冬季纳潮能力增大。“潭洲-前航道”作为连接虎门河口和西江主干道上游的纽带, 中下游浮标厂以下河段主要受控于潮流, 虽然北江流量增大且ΔZDIS增大, 但由于虎门河口的潮动力增强, 上游“澜石-紫洞”河段的S(t)贡献率明显减小(平均为15%), 因此调整期阶段该体系的纳潮能力亦有所增强。
马玉婷, 蔡华阳, 杨昊, 等, 2022. 珠江磨刀门河口水位分布演变特征及其对人类活动的响应. 热带海洋学报, 41(2): 52-64 |
王博芝, 李博, 魏稳, 等, 2022. 珠江河网典型横向汊道水面线演变及成因. 浙江大学学报(工学版), 56(7): 1375-1384 |
王博芝, 杨昊, 欧素英, 等, 2021. 珠江河网横向汊道水面线演变过程及原因探讨——以东平水道为例. 热带地理, 41(2): 410-422 |
刘宏霄, 罗敬思, 徐治中, 2019. 西江下游航道整治工程效益分析. 珠江水运, (14): 61-62 DOI:10.14125/j.cnki.zjsy.2019.14.022 |
刘俊勇, 2014. 珠江三角洲河网主要节点分类与作用分析. 人民珠江, 35(6): 48-54 DOI:10.3969/j.issn.1001-9235.2014.06.015 |
李博, 杨昊, 欧素英, 等, 2022. 珠江磨刀门河口潮波振幅梯度与上下游动力边界的关系异变研究. 海洋与湖沼, 53(3): 513-527 |
杨昊, 欧素英, 傅林曦, 等, 2020. 珠江磨刀门河口日均水位变化及影响因子辨识. 水利学报, 51(7): 869-881 |
吴超羽, 2018. 珠江三角洲千年尺度演变的动态平衡及其唯象判据探讨. 海洋学报, 40(7): 22-37 |
何为, 2012. 珠江河口分汊机制及其对排洪和咸潮上溯的影响[D]. 上海: 华东师范大学: 15.
|
张先毅, 杨昊, 黄竞争, 等, 2020. 强人类活动驱动下珠江磨刀门河口径潮动力的季节性异变特征. 海洋与湖沼, 51(5): 1043-1054 |
欧素英, 杨清书, 杨昊, 等, 2017. 河口三角洲径流和潮汐相互作用模型及应用. 热带海洋学报, 36(5): 1-8 |
易小兵, 王世俊, 李春初, 2008. 珠江河口界面特征与河口管理理念. 海洋学研究, 26(4): 86-92 |
郑国栋, 2005. 人类活动对珠江三角洲水动力环境影响研究[D]. 武汉: 武汉大学: 50-51.
|
黄镇国, 张伟强, 2004. 人为因素对珠江三角洲近30年地貌演变的影响. 第四纪研究, (4): 394-401 |
谢梅芳, 张萍, 杨昊, 等, 2021. 珠江"伶仃洋河口湾-虎门-潮汐通道"的潮波传播特征. 热带海洋学报, 40(4): 1-13 |
ALEBREGTSE N C, DE SWART H E, 2016. Effect of river discharge and geometry on tides and net water transport in an estuarine network, an idealized model applied to the Yangtze Estuary. Continental Shelf Research, 123: 29-49 |
BUSCHMAN F A, HOITINK A J F, VAN DER VEGT M, et al, 2009. Subtidal water level variation controlled by river flow and tides. Water Resources Research, 45(10): W10420 |
CAI H Y, SAVENIJE H H G, JIANG C J, et al, 2016. Analytical approach for determining the mean water level profile in an estuary with substantial fresh water discharge. Hydrology and Earth System Sciences, 20(3): 1177-1195 |
CAI H, SAVENIJE H H G, TOFFOLON M, 2014. Linking the river to the estuary: influence of river discharge on tidal damping. Hydrology and Earth System Sciences, 18(1): 287-304 |
CAI H Y, SAVENIJE H H G, YANG Q S, et al, 2012. Influence of river discharge and dredging on tidal wave propagation: modaomen estuary case. Journal of Hydraulic Engineering, 138(10): 885-896 |
GUO L C, VAN DER WEGEN M, JAY D A, et al, 2015. River-tide dynamics: Exploration of nonstationary and nonlinear tidal behavior in the Yangtze River estuary. Journal of Geophysical Research: Oceans, 120(5): 3499-3521 |
HOITINK A J F, WANG Z B, VERMEULEN B, et al, 2017. Tidal controls on river delta morphology. Nature Geoscience, 10(9): 637-645 |
JAY D A, FLINCHEM E P, 1997. Interaction of fluctuating river flow with a barotropic tide: a demonstration of wavelet tidal analysis methods. Journal of Geophysical Research: Oceans, 102(C3): 5705-5720 |
KENNEDY J, EBERHART R, 1995. Particle swarm optimization [C] // Proceedings of ICNN'95 - International Conference on Neural Networks. Perth, WA, Australia: IEEE: 1942-1948.
|
KUKULKA T, JAY D A, 2003. Impacts of Columbia River discharge on salmonid habitat: 1. A nonstationary fluvial tide model. Journal of Geophysical Research: Atmospheres, 108(C9): 3293 |
LUO X L, ZENG E Y, JI R Y, et al, 2007. Effects of in-channel sand excavation on the hydrology of the Pearl River Delta, China. Journal of Hydrology, 343(3/4): 230-239 |
MATTE P, JAY D A, ZARON E D, 2013. Adaptation of classical tidal harmonic analysis to nonstationary tides, with application to River Tides. Journal of Atmospheric and Oceanic Technology, 30(3): 569-589 |
MATTE P, SECRETAN Y, MORIN J, 2014. Temporal and spatial variability of tidal-fluvial dynamics in the St. Lawrence fluvial estuary: an application of nonstationary tidal harmonic analysis. Journal of Geophysical Research: Oceans, 119(9): 5724-5744 |
MOFTAKHARI H R, JAY D A, TALKE S A, 2016. Estimating river discharge using multiple tide gauges distributed along a channel. Journal of Geophysical Research: Oceans, 121(4): 2078-2097 |
PAN H D, GUO Z, WANG Y Y, et al, 2018a. Application of the EMD method to river tides. Journal of Atmospheric and Oceanic Technology, 35(4): 809-819 |
PAN H D, LV X Q, 2019. Reconstruction of spatially continuous water levels in the Columbia River Estuary: The method of Empirical Orthogonal Function revisited. Estuarine, Coastal and Shelf Science, 222: 81-90 |
PAN H D, LV X Q, WANG Y Y, et al, 2018b. Exploration of tidal-fluvial interaction in the Columbia River Estuary Using S_TIDE. Journal of Geophysical Research: Oceans, 123(9): 6598-6619 |
PAWLOWICZ R, BEARDSLEY B, LENTZ S, 2002. Classical tidal harmonic analysis including error estimates in MATLAB using T_TIDE. Computers & Geosciences, 28(8): 929-937 |
ZHANG P, YANG Q S, PAN H D, et al, 2021b. Impacts of human interventions on the seasonal and nodal dynamics of the M2 and K1 tidal constituents in Lingdingyang Bay of the Zhujiang River Delta, China. Acta Oceanologica Sinica, 40(10): 49-64 |
ZHANG P, YANG Q S, WANG H, et al, 2021a. Stepwise alterations in tidal hydrodynamics in a highly human-modified estuary: the roles of channel deepening and narrowing. Journal of Hydrology, 597: 126153 |
ZHANG W, XU Y, HOITINK A J F, et al, 2015. Morphological change in the Pearl River Delta, China. Marine Geology, 363: 202-219 |
 2023, Vol. 54
2023, Vol. 54


