
中国海洋湖沼学会主办。
文章信息
- 何英, 汪嘉宁, 王凡. 2023.
- HE Ying, WANG Jia-Ning, WANG Fan. 2023.
- 基于数值模式评估细尺度参数化方案在南大洋背风波生成源地的适用性
- NUMERICAL MODEL-BASED ASSESSMENT ON APPLICABILITY OF FINE-SCALE PARAMETERIZATION AT GENERATION SITE OF INTERNAL LEE WAVES IN THE SOUTHERN OCEAN IN NUMERICAL MODEL
- 海洋与湖沼, 54(3): 679-688
- Oceanologia et Limnologia Sinica, 54(3): 679-688.
- http://dx.doi.org/10.11693/hyhz20221000263
文章历史
-
收稿日期:2022-10-17
收修改稿日期:2022-12-29
2. 中国科学院海洋环流与波动重点实验室 山东青岛 266071;
3. 中国科学院大学 北京 100049;
4. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室 山东青岛 266237
2. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Laboratory for Ocean Dynamics and Climate, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China)
经圈翻转环流在世界各大洋盆之间传输热量和溶解物质, 因此在全球气候系统中扮演着极其重要的角色。目前普遍认为经圈翻转环流的上翻分支主要受跨等密度面湍流混合(在下文中简记为“湍流混合”)的控制, 湍流混合为热量的向下扩散作出了突出贡献, 使得底层水密度减小, 逐渐上升至海表面(Talley, 2013)。过去的观测研究发现湍流混合的强度在全球大洋中分布极不均匀(Polzin et al, 1997; Ledwell et al, 2000)。同时, 前人的数值模拟研究表明湍流混合的空间分布显著影响着经圈翻转环流的强度和结构(Jayne, 2009; Oka et al, 2013)。因此, 为了更准确地预测全球气候变化, 探索大洋中湍流混合的空间分布情况是亟不可待的。目前, 对湍流混合强度最为精确的测量方法是使用微尺度垂直剖面仪获取微尺度的流速剪切数据, 再对微尺度数据进行处理得到湍流动能耗散率(在下文中简记为“耗散率”), 此观测手段通常被称为混合直接观测。然而, 微尺度垂直剖面仪的价格十分昂贵, 而且其布放依赖于科考航次, 因此通过直接观测了解到的湍流混合分布只是冰山一角。
大洋中的湍流混合主要来自海洋内波的破碎(MacKinnon et al, 2017)。得益于GM (Garrett-Munk)大洋内波普适谱的发展(Garrett et al, 1972, 1975), 一系列用于估算湍流混合强度的细尺度参数化方案逐渐得到发展。首先, Henyey等(1986)假设耗散率等同于内波谱跨越截止垂直波数的净能量通量, 提出了HWF (Henyey-Wright-Flatte)模型。根据HWF模型, 耗散率可以利用尺度为O (10~100 m)的表征内波活动的细尺度剪切或应变的谱级与对应的GM谱级的比值来估算。随后, Gregg(1989)和Wijesekera等(1993)根据HWF模型分别提出了基于细尺度剪切数据的G89 (Gregg 1989)方案和基于细尺度应变数据的W93 (Wijesekera 1993)方案。在HWF模型中, 局地内波谱的形状被假定为与GM谱一致。然而在深海的强内波生成源地附近, 实测内波场常常与GM谱相比发生了变形, 能量可能会向生成内波的频率处集中(Pollmann, 2020; Takahashi et al, 2021)。考虑到这一点, Polzin等(1995)引入剪切应变方差比Rω对HWF模型应用了频率矫正, 提出了GHP (Gregg-Henyey-Polzin)方案。最近, Ijichi等(2015)发现GHP方案不恰当地对宽频段的内波谱应用了单波近似, 也因此当内波谱存在突出的近惯性峰值时(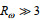
在南大洋, 南极绕极流的强底部流速会与粗糙海底地形相互作用生成大量背风波(Cusack et al, 2017)。前人基于细尺度参数化方案证实了南大洋的粗糙海底上方存在背风波破碎导致的增强混合(Garabato et al, 2004; Sloyan, 2005; Wu et al, 2011)。近年来, 有研究通过将GHP方案的结果与混合直接观测结果进行比对, 发现GHP方案明显高估了南大洋中背风波生成源地处的实际混合强度, 最大误差可达一个量级, 然而导致这种误差的原因仍不明确(Sheen et al, 2013; Waterman et al, 2014)。
目前的大多数混合间接观测研究是从波波相互作用机制的角度来判断细尺度参数化方案在不同海域的适用性, 认为单一种类的方案不适用于某海域即说明细尺度参数化方案的基本原理在该海域不成立, 忽略了不同种类的细尺度参数化方案之间的性能差别。在本文中, 我们采用包含背景GM内波场的高分辨率数值模式来模拟背风波的生成、背风波与背景GM内波场的非线性相互作用以及背风波的破碎过程, 然后根据模式结果验证四种细尺度参数化方案在南大洋的背风波生成源地的适用性, 最后重点探讨了导致GHP方案和IH方案在南大洋的背风波生成源地存在显著性能差别的原因。
1 研究方法 1.1 模式设置本研究中我们使用的是麻省理工学院开发的具有非静力近似能力的大气海洋环流模式MITgcm (Massachusetts Institute of Technology General Circulation Model)(Marshall et al, 2012)。模型的初始扰动流速场和扰动密度场为背景GM内波场。为了尽可能地允许不同尺度的内波进行非线性相互作用, 我们采用了垂直二维数值模式, 其水平分辨率Δx为50 m, 垂直分辨率Δz为5 m。模型的高度设置为南大洋的平均深度4 km, 而模型的宽度设置为90 km, 以保证能在模型中引入背景GM内波场的近惯性分量。我们在模型的侧边界使用了循环边界条件, 在底边界使用了无摩擦边界条件。在模型中, 我们将局地惯性频率f和背景浮性频率N设置为南大洋深海的典型值1.26×10–4 rad/s和1.14×10–3 rad/s (Sheen et al, 2013)。为了模拟背风波的生成, 我们在模式中加入了无垂直剪切的纬向稳定流和高度呈单色正弦曲线分布的海底地形。根据南大洋中的背风波主要生成源地——德雷克海峡处的典型值, 底部流速U0、海底地形高度hT和海底地形波长λH分别被设置为0.2 m/s、80 m和2 km (Sheen et al, 2013)。此外, 我们还在模型的经向动量方程中增加了一个体积力U0×f0, 用来充当与稳定流在所有深度上维持平衡所必需的正压梯度力。对于数值模式, 背景黏度系数和扩散系数的选取非常关键, 最理想的选择是满足模式稳定性要求的最小数值。在本研究中, 为了抑制网格状非光滑地形引起的网格噪声, 我们在垂直上使用Laplacian类型的背景黏度系数和扩散系数(AV=10−5 m2/s; KV=10−5 m2/s), 但在水平上使用MITgcm提供的Biharmonic类型的背景黏度系数和扩散系数(A4H=102 m4/s; K4H=102 m4/s)。需要注意的是模式中设置的背景扩散系数并不等同于与内波破碎相关的湍流扩散系数。模式的基本设置如图 1所示, 而模式中的参数值如表 1所示。
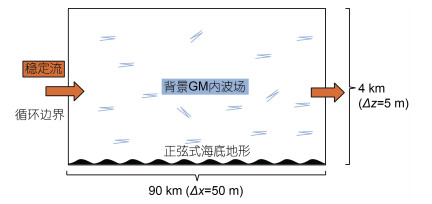 |
| 图 1 数值模式设置示意图 Fig. 1 Schematic of the model settings 注: 橘色箭头表示稳定流; 蓝色折线表示背景GM (Garret-Munk)内波场; 黑色填色表示高度呈正弦式分布的海底地形; Δx为水平分辨率; Δz为垂直分辨率 |
| 参数名称 | 参数符号 | 设定值 |
| 惯性频率 | f | 1.26×10–4 rad/s |
| 浮性频率 | N | 1.14×10–3 rad/s |
| 重力加速度 | g | 9.8 m/s2 |
| 参考水密度 | ρ0 | 1 000 kg/m3 |
| 水平黏性系数 | A4H | 102 m4/s |
| 垂直黏性系数 | AV | 10–5 m2/s |
| 水平扩散系数 | K4H | 102 m4/s |
| 垂直扩散系数 | KV | 10–5 m2/s |
| 稳定流流速 | U0 | 0.2 m/s |
| 海底地形高度 | hT | 80 m |
| 海底地形波长 | λH | 2 km |
由于GM谱的构建过程中引入了以下假设: (1) 观测所得脉动量的时间或空间序列是满足统计平稳性和水平各向同性的随机过程; (2) 观测所得脉动量的时间或空间序列是由众多具有不同频率、不同波数、不同振幅和相位随机的内进行波叠加而成的; (3) 内波场中向上传播和向下传播的内波能量通量相等(Garrett et al, 1972, 1975)。在MITgcm中引入二维GM内波场的流程为: 首先我们将内波场设定为是由一系列具有不同水平模态(n)和垂直模态(j)的具有随机相位的内波分量组成, 接着我们根据水平模态和垂直模态的大小, 将每个内波分量的能量密度设为GM79模型(Munk, 1981)的对应值。
GM79模型的表达式为
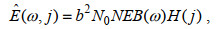 (1)
(1) (2)
(2)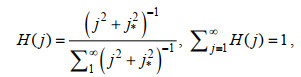 (3)
(3)其中, b=1 300 m, N0=5.24×10−3 rad/s, E=6.3×10−5, j*=3为常数, f表示惯性频率, N表示浮性频率, B(ω)和H(j)分别刻画了能量(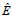
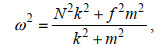 (4)
(4)我们可以作出如下变换
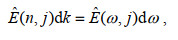 (5)
(5)由此得到
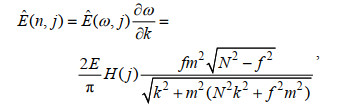 (6)
(6)其中,
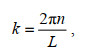 (7)
(7)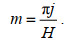 (8)
(8)接着, 我们将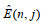
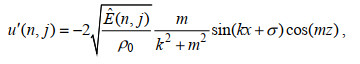 (9)
(9)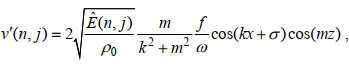 (10)
(10)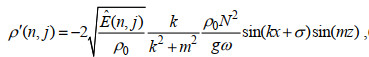 (11)
(11)其中ρ0为参考水体密度, g为重力加速度。GM内波场的水平扰动速度场的标准差大约为0.03 m/s (Munk, 1981)。需要注意的是每个内波分量的相位σ都是随机给定的。同时, 为了保证内波场满足水平各向同性, 参照Iwamae等(2009), 我们通过调节水平模态n的正负值, 令向左与向右传播的具有相同水平波数的内波数量相当。之后, 我们将所有内波分量的扰动量值进行累加, 便得到了GM内波场的扰动速度场和扰动密度场
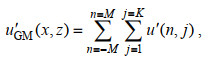 (12)
(12)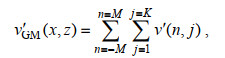 (13)
(13)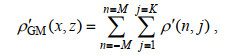 (14)
(14)其中, M和K分别为人为设定的水平模态和垂直模态的最大值。
为了在模式中加入准稳定的背景GM内波场, 按照Hibiya等(2002)的做法, 我们首先计算第0~900水平模态和第1~500垂直模态的具有随机相位的线性内波之间在10个惯性周期(注: 惯性周期在前人的研究中常被简称为Ti)内的非线性相互作用。在GM内波场达到准稳定后, 我们再利用一个惯性周期(t=10Ti ~11Ti)在整个模型域中逐渐建立起稳定流, 最后再将模型运行9个惯性周期(t=11Ti ~20Ti)。
1.3 根据细尺度参数化方案求耗散率在本文中, 我们分别验证了G89、W93、GHP和IH方案的适用性, 这四种细尺度参数化方案的表达式如下所示
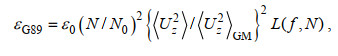 (15)
(15)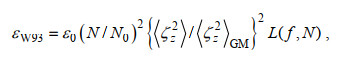 (16)
(16)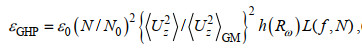 (17)
(17)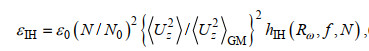 (18)
(18)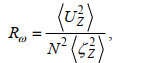 (19)
(19)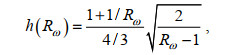 (20)
(20)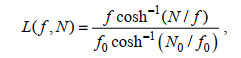 (21)
(21)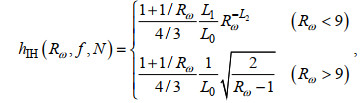 (22)
(22)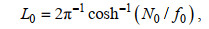 (23)
(23)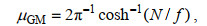 (24)
(24)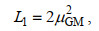 (25)
(25)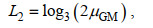 (26)
(26)其中, ε0为对应GM内波场的常数耗散率6.73×10−10 W/kg, f0为7.29×10−5 rad/s, 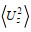
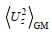
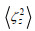
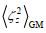
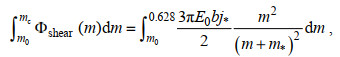 (27)
(27)其中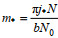
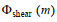
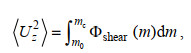 (28)
(28) (29)
(29)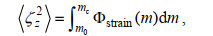 (30)
(30)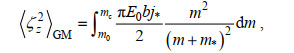 (31)
(31)其中, 
对于每一个数值实验, 我们使用模式的动能方程中的耗散项来估算第20个惯性周期时刻(t=20Ti)的耗散率ε。下列方程为动能方程的耗散项的表达式:
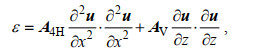 (32)
(32)其中, u是一个速度矢量, 包括经向、纬向和垂直流速分量。为了与细尺度参数化方案求得的耗散率进行对比, 对公式(32)求出的耗散率剖面也进行了每490 m深度范围内的垂直平均。在本研究中, 通过将来自参数化方案的结果与来自公式(32)的结果进行比较, 来评估各参数化方案的性能。需要注意的是, 由于模式的东西边界为循环边界, 因此下文中的耗散率剖面都是进行水平平均后再进行讨论。
2 结果与讨论 2.1 背风波与背景内波场之间的非线性相互作用图 2和图 3是用层结标准化后的剪切谱(又称弗劳德谱)的时间序列。每个弗劳德谱是在1 800个水平网格点上用从海面到海底的数据计算出的弗劳德谱的平均值。如图 2所示, 随着线性内波分量之间的非线性相互作用的开始, 弗劳德谱的结构开始被改变。在t=4Ti (注: Ti为惯性周期的简称, 在本研究中1Ti约等于50 400 s)。之后, 弗劳德谱变得准稳定, 并在垂直波数约0.063 rad/m处形成了谱斜率的“转降”, 这可能是强烈的非线性作用导致的(Gargett et al, 1981)。如图 3所示, 在t=10Ti之后, 模型中加载了稳定流, 可以发现, 当t=12Ti时, 一个谱峰出现在了垂直波数约0.005 rad/m的位置, 这恰好对应着海底产生的背风波的初始垂直波数。随着模式计算的进行, 谱级在整个垂直波数范围内都显著提高, 这可能是由背风波和背景GM内波场之间的非线性相互作用所引起的能量串级现象。同时, 随着谱级的提升, “转降”垂直波数转移到了较低的垂直波数0.025 rad/m上。
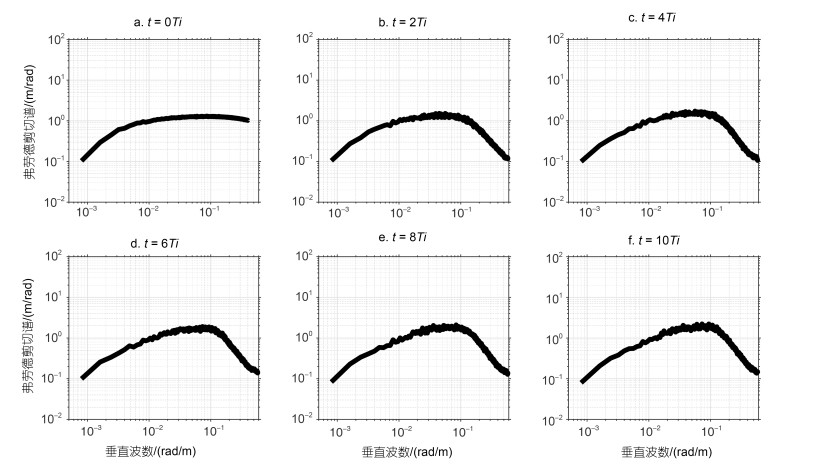 |
| 图 2 在数值模式中加入稳定流前(t=0Ti~10Ti), 垂直波数弗劳德谱随时间的变化 Fig. 2 Time variations of the vertical wave number Froude spectrum in numerical model before setup of the steady flow in the model (t=0Ti~10Ti) |
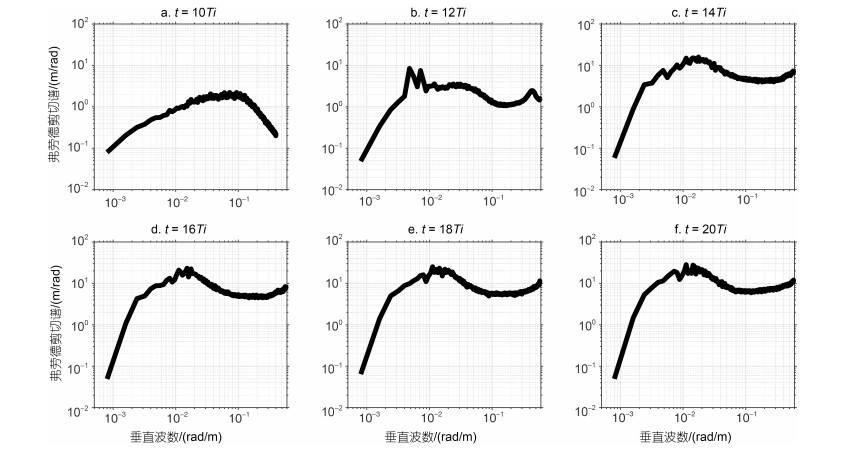 |
| 图 3 在数值模式中加入稳定流后(t=10Ti~20Ti), 垂直波数弗劳德谱随时间的变化 Fig. 3 Time variations of the vertical wave number Froude spectrum in numerical model after setup of the steady flow in the model (t=10Ti~20Ti) |
Nikurashin等(2010)的模拟研究曾显示背风波的生成和破碎伴随着海底上方近惯性内波的增强, 这是因为背风波在与近惯性内波发生相互作用时, 会传递一部分能量以加速近惯性内波。参考Nikurashin等(2010)的方法, 我们检查了纬向平均扰动流速的随时间的变化。如图 4所示, 纬向平均扰动流速的大小和符号呈近惯性周期变化, 这说明模式中存在近惯性内波。而且在背风波生成之后(t = 10Ti~11Ti), 海底上方出现近惯性内波的纬向振幅随时间增大的现象, 这与Nikurashin等(2010)的模拟结果相一致。为了更清楚地展示数值实验中的物理过程, 我们给出了纬向扰动流速场随时间的变化情况。当t=10Ti时, 模式域被准稳定的背景GM内波场所占据(图 5a)。当模型中加入水平稳定流后(t=12Ti), 可以看到背风波波束穿过背景GM内波场向上传播(图 5b)。随着时间的推移(t=17Ti), 距海底上方0~1 000 m的深度范围内出现了叠加在背风波波束上的强水平流动, 对应着强近惯性内波的纬向流速分量(图 5c)。此外, 我们还计算了t=20Ti时刻的理查森(Richardson)数(Ri=N2/S2, 其中S2=(∂u/∂z)2+(∂v/∂z)2是垂直流速剪切的平方)的空间分布情况。如图 5d所示, 模式域中零星出现了理查森数小于临界值0.25的区域, 尤其是在强近惯性内波存在的距海底上方0~1 000 m的深度范围内更为集中。这意味着海底生成的背风波在向上传播过程中, 因为与海底附近的近惯性内波发生相互作用, 而在海底上方很短的距离内就因为垂直剪切不稳定而发生破碎。
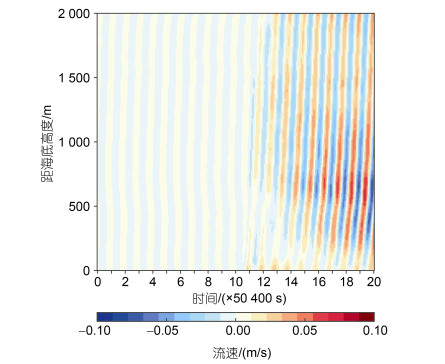 |
| 图 4 数值模式中纬向平均扰动流速随时间的演变 Fig. 4 Time evolution of zonal mean perturbation velocity in the numerical model 注: 1Ti约等于50 400 s |
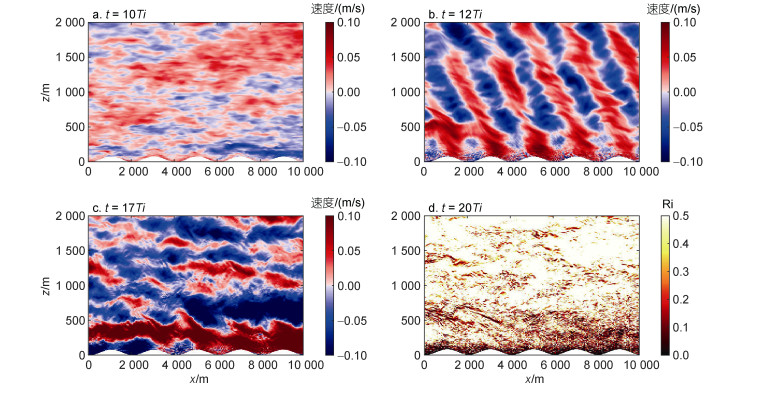 |
| 图 5 背风波的生成、传播与破碎 Fig. 5 The generation, propagation, and breaking of internal lee waves 注: Ri表示理查森(Richardson)数 |
我们首先讨论基于剪切的G89方案和基于应变的W93方案的性能。如图 6所示, G89方案在整个深度上都高估了耗散率, 尤其是在距海底0~490 m和2 990~3 490 m的深度范围内, 来自G89方案的结果与来自耗散项式(32)的结果差距能达到6倍。反之, W93方案在整个深度上都低估了耗散率, 但是整体上性能比G89方案要好很多, 即使是差距最大的距海底0~490 m深度范围内, 来自参数化方案的结果和来自耗散项的结果的差距也在3倍范围内。正如在引言中所介绍的, G89方案和W93方案都是假定内波谱的形状与GM谱一致, 所以图 6所示的误差可能是由于内波谱相对于GM谱发生变形所导致的。
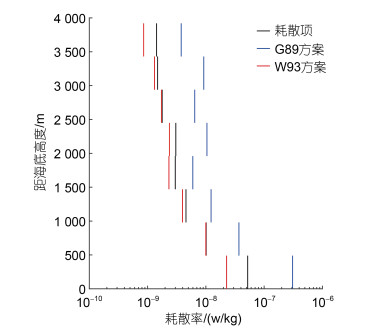 |
| 图 6 从耗散项(黑色)、基于剪切的G89参数化方案(蓝色)和基于应变的W93参数化方案(红色)得到的纬向平均耗散率垂直分布的差异 Fig. 6 Differences among the zonal-mean vertical distributions of dissipation rates obtained from the dissipation term (black), the shear-based G89 parameterization (blue), and the strain-based W93 parameterization (red) |
内波场能量在频域上的分布情况可以用剪切方差应变比Rω来衡量, 这是因为Rω也代表着内波场动能与势能的比值。对于GM谱, Rω为常数3, 这意味着, 当Rω偏离3时, 内波谱就相对GM谱发生了变形。前人在南大洋的观测研究显示Rω有着剧烈的空间变化, 而且在海底上方远大于3 (Sheen et al, 2013)。图 7则展示了我们的模式中Rω的垂直分布情况, 可以发现在整个深度范围内, Rω都大于3, 尤其是在距海底0~490 m的范围内, Rω高达11, 这是因为该深度存在强近惯性内波(图 5c)。这说明内波场相对于GM内波场向低频偏转, 内波场相对于GM内波场具有更大的动能比例。在这种情况下, 由于G89方案是通过流速剪切(动能)和常数Rω=3来评估内波场的总能量水平, 因此G89方案会高估内波场的总能量, 从而高估对应的耗散率。反之, 由于W93方案是通过应变(势能)和常数Rω=3来评估内波场的总能量水平, 因此W93方案会低估内波场的总能量, 从而低估对应的耗散率。这与图 6显示的G89方案和W93方案的误差一致。
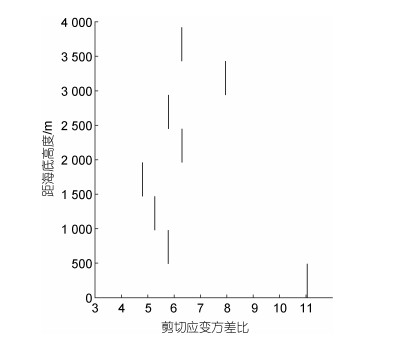 |
| 图 7 剪切方差应变比Rω的纬向平均垂直分布情况 Fig. 7 The zonal-mean vertical distribution of shear-strain variance ratio Rω |
接下来, 我们分析包含频率矫正项的GHP方案和IH方案的性能, GHP方案中的频率矫正项的表达式为公式(20), IH方案中的频率矫正项的表达式为公式(22)~(26)。如图 8所示, GHP方案虽然考虑了内波谱相对于GM谱的变形, 但在全水深范围内对耗散率有所高估, 与W93方案相比性能没有明显提升。相较于GHP方案, IH方案的性能要好很多, 与来自耗散项的结果的差距在两倍范围内。特别是在剪切方差应变比Rω较大的距海底0~490 m和2 990~3 490 m的深度范围内, IH方案比GHP方案明显更接近来自耗散项式(32)的结果。这表明, 尽管GHP方案是目前应用最为广泛的细尺度参数化方案, 但是对频率矫正项作出变换的IH方案对耗散率的估计会更准确一些。前人发现GHP方案明显高估了南大洋中背风波生成源地处的实际混合强度(Sheen et al, 2013; Waterman et al, 2014), 根据本研究, 我们推测使用IH参数化方案会在一定程度上缩小这种误差。
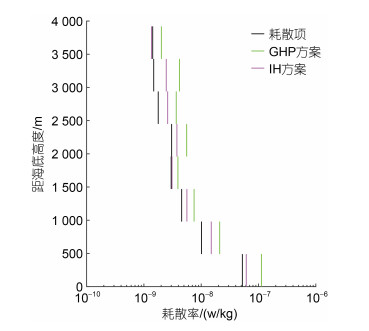 |
| 图 8 从耗散项(黑色)、GHP参数化方案(绿色)和IH参数化方案(玫红色)得到的耗散率纬向平均垂直分布的差异 Fig. 8 Differences among the zonal-mean vertical distributions of dissipation rates obtained from the dissipation term (black), the GHP parameterization (green), and the IH parameterization (magenta) |
湍流混合是控制经圈翻转环流的重要因子, 了解湍流混合在全球大洋的空间分布情况对预测气候变化来说至关重要。由于获取混合的直接观测数据难度较大, 前人发展了一系列基于GM大洋内波普适谱的细尺度参数化方案来估算混合强度。前人通过将细尺度参数化方案的结果与混合直接观测数据做比较, 验证了细尺度参数化方案在不同海域的适用性。本研究聚焦于细尺度参数化方案在南大洋背风波生成源地处的适用性, 创新性地使用高分辨率数值模式来模拟背风波与背景GM内波场的非线性相互作用过程, 并根据模式结果首先评估了没有考虑内波场相对于GM内波场的变形的G89方案和W93方案的性能, 然后评估了考虑了内波场相对于GM内波场的变形的GHP和IH方案的性能。
我们发现, 基于剪切的G89方案会明显高估耗散率, 而基于应变的W93方案会低估耗散率。这是因为, 背风波的生成伴随着海底上方近惯性内波的增强, 使得内波场相对于GM内波场向低频偏转, 剪切(动能)与应变(势能)的比值增大。在这种情况下, G89方案会高估内波场的总能量及其对应的耗散率。反之, 由于W93方案会低估内波场的总能量及其对应的耗散率。此外, 我们发现, 已经考虑了内波谱的变形GHP方案仍然会高估耗散率, 但对GHP方案中的频率矫正项作出变换的IH方案能很好评估耗散率值。基于本研究, 我们提出细尺度参数化方案的选取对于研究背风波生成源地处的混合强度来说非常关键。前人使用GHP方案明显高估了南大洋中背风波生成源地处的实际混合强度(Sheen et al, 2013; Waterman et al, 2014), 我们推测使用最新发展的IH参数化方案能有效缩小这种误差。
需要强调的是, 本研究仍然存在一些遗留问题需要进一步研究。第一, 鉴于在真实大洋中, 南极绕级流的垂直流速剪切与背景内波场相比较弱, 我们假设模型中的稳定流没有垂直流速剪切。考虑到波-流相互作用过程也会影响细尺度参数化方案的适用性(Waterman et al, 2014), 我们计划下一步在模式中加入平均流剪切来进一步讨论在不同的剪切强度的情况下, 细尺度参数化方案的适用性。第二, 由于受计算资源的限制, 本文的数值模拟局限在垂直二维空间。考虑到一些海流可能绕过而不是流过海底地形(Nikurashin et al, 2014), 以及一部分内波之间的相互作用可能是三维过程, 我们计划在未来将本研究内容拓展到三维空间。第三, 由于我们在模型中使用的是理想化的单色正弦地形以及循环东西边界, 本文中耗散率的量级并不能与真实南大洋中的耗散率量级相提并论。因此, 我们只能定性地考量而不能定量地评估各个参数化方案的性能。尽管本研究存在以上问题仍未解决, 但我们相信本研究为验证细尺度参数化方案的适用性提供了新的思路, 也就是不依赖于现场观测数据, 而是使用包含背景GM内波场的模式从理论角度评估混合参数化方案的适用性。而且本研究为背风波生成源地的混合研究提供了细尺度参数化方案的选择依据, 这对于湍流混合研究来说非常重要。
CUSACK J M, GARABATO A C N, SMEED D A, et al, 2017. Observation of a large lee wave in the Drake Passage. Journal of Physical Oceanography, 47(4): 793-810 DOI:10.1175/jpo-d-16-0153.1 |
GARABATO A C N, POLZIN K L, KING B A, et al, 2004. Widespread intense turbulent mixing in the Southern Ocean. Science, 303(5655): 210-213 DOI:10.1126/science.1090929 |
GARGETT A E, HENDRICKS P J, SANFORD T B, et al, 1981. A composite spectrum of vertical shear in the upper ocean. Journal of Physical Oceanography, 11(9): 1258-1271 DOI:10.1175/1520-0485(1981)011<1258:Acsovs>2.0.Co;2 |
GARRETT C, MUNK W, 1972. Space-time scales of internal waves. Geophysical Fluid Dynamics, 3(3): 225-264 DOI:10.1080/03091927208236082 |
GARRETT C, MUNK W, 1975. Space-time scales of internal waves: a progress report. Journal of Geophysical Research, 80(3): 291-297 DOI:10.1029/JC080i003p00291 |
GREGG M C, 1989. Scaling turbulent dissipation in the thermocline. Journal of Geophysical Research: Oceans, 94(C7): 9686-9698 DOI:10.1029/JC094iC07p09686 |
HIBIYA T, NAGASAWA M, NIWA Y, 2002. Nonlinear energy transfer within the oceanic internal wave spectrum at mid and high latitudes. Journal of Geophysical Research: Oceans, 107(C11): 3207 DOI:10.1029/2001jc001210 |
HENYEY F S, WRIGHT J, FLATTE S M, 1986. Energy and action flow through the internal wave field: An eikonal approach. Journal of Geophysical Research: Oceans, 91(C7): 8487-8495 DOI:10.1029/JC091iC07p08487 |
IJICHI T, HIBIYA T, 2015. Frequency-based correction of finescale parameterization of turbulent dissipation in the deep ocean. Journal of Atmospheric and Oceanic Technology, 32(8): 1526-1535 DOI:10.1175/jtech-d-15-0031.1 |
IWAMAE N, HIBIYA T, WATANABE M, 2009. Numerical study of the bottom-intensified tidal mixing using an "eikonal approach". Journal of Geophysical Research: Oceans, 114(D5): C05022 DOI:10.1029/2008jc005130 |
JAYNE S R, 2009. The impact of abyssal mixing parameterizations in an ocean general circulation model. Journal of Physical Oceanography, 39(7): 1756-1775 DOI:10.1175/2009jpo4085.1 |
JING Z, WU L X, LI L, et al, 2011. Turbulent diapycnal mixing in the subtropical northwestern Pacific: spatial-seasonal variations and role of eddies. Journal of Geophysical Research: Oceans, 116(C10): C10028 DOI:10.1029/2011jc007142 |
LEDWELL J R, MONTGOMERY E T, POLZIN K L, et al, 2000. Evidence for enhanced mixing over rough topography in the abyssal ocean. Nature, 403(6766): 179-182 DOI:10.1038/35003164 |
LI Y, XU Y S, 2014. Penetration depth of diapycnal mixing generated by wind stress and flow over topography in the northwestern Pacific. Journal of Geophysical Research: Oceans, 119(8): 5501-5514 DOI:10.1002/2013jc009681 |
MACKINNON J A, ZHAO Z X, WHALEN C B, et al, 2017. Climate process team on internal wave-driven ocean mixing. Bulletin of the American Meteorological Society, 98(11): 2429-2454 DOI:10.1175/bams-d-16-0030.1 |
MARSHALL J, SPEER K, 2012. Closure of the meridional overturning circulation through Southern Ocean upwelling. Nature Geoscience, 5(3): 171-180 DOI:10.1038/ngeo1391 |
Munk W H, 1981. Internal waves and small-scale processes[M]//Warren B A, Wunsch C. Evolution of Physical Oceanography. MIT Press: 264-291.
|
NIKURASHIN M, FERRARI R, 2010. Radiation and dissipation of internal waves generated by geostrophic motions impinging on small-scale topography: theory. Journal of Physical Oceanography, 40(5): 1055-1074 DOI:10.1175/2009jpo4199.1 |
NIKURASHIN M, FERRARI R, GRISOUARD N, et al, 2014. The impact of finite-amplitude bottom topography on internal wave generation in the Southern Ocean. Journal of Physical Oceanography, 44(11): 2938-2950 DOI:10.1175/Jpo-D-13-0201.1 |
OKA A, NIWA Y, 2013. Pacific deep circulation and ventilation controlled by tidal mixing away from the sea bottom. Nature Communications, 4: 2419 DOI:10.1038/ncomms3419 |
POLLMANN F, 2020. Global characterization of the ocean's internal wave spectrum. Journal of Physical Oceanography, 50(7): 1871-1891 DOI:10.1175/Jpo-D-19-0185.1 |
POLZIN K L, TOOLE J M, LEDWELL J R, et al, 1997. Spatial variability of turbulent mixing in the abyssal ocean. Science, 276(5309): 93-96 DOI:10.1126/science.276.5309.93 |
POLZIN K L, TOOLE J M, SCHMITT R W, 1995. Finescale parameterizations of turbulent dissipation. Journal of Physical Oceanography, 25(3): 306-328 DOI:10.1175/1520-0485(1995)025<0306:Fpotd>2.0.Co;2 |
SHEEN K L, BREARLEY J A, NAVEIRA GARABATO A C, et al, 2013. Rates and mechanisms of turbulent dissipation and mixing in the Southern Ocean: results from the Diapycnal and Isopycnal Mixing Experiment in the Southern Ocean (DIMES). Journal of Geophysical Research: Oceans, 118(6): 2774-2792 DOI:10.1002/jgrc.20217 |
SLOYAN B M, 2005. Spatial variability of mixing in the Southern Ocean. Geophysical Research Letter, 32(18): L18603 DOI:10.1029/2005gl023568 |
TAKAHASHI A, HIBIYA T, 2021. Influence of the distortion of vertical wavenumber spectra on estimates of turbulent dissipation using the finescale parameterization: observations in the Antarctic circumpolar current. Journal of Geophysical Research: Oceans, 126(6): e2020JC016613 DOI:10.1029/2020JC016613 |
TALLEY L D, 2013. Closure of the global overturning circulation through the Indian, Pacific, and Southern Oceans: schematics and transports. Oceanography, 26(1): 80-97 DOI:10.5670/oceanog.2013.07 |
WATERMAN S, POLZIN K L, GARABATO A C N, et al, 2014. Suppression of internal wave breaking in the Antarctic Circumpolar Current near topography. Journal of Physical Oceanography, 44(5): 1466-1492 DOI:10.1175/jpo-d-12-0154.1 |
WHALEN C B, MACKINNON J A, TALLEY L D, 2018. Large-scale impacts of the mesoscale environment on mixing from wind-driven internal waves. Nature Geoscience, 11(11): 842-847 DOI:10.1038/s41561-018-0213-6 |
WIJESEKERA H, PADMAN L, DILLON T, et al, 1993. The application of internal-wave dissipation models to a region of strong mixing. Journal of Physical Oceanography, 23(2): 269-286 DOI:10.1175/1520-0485(1993)023<0269:taoiwd>2.0.co;2 |
WU L X, JING Z, RISER S, et al, 2011. Seasonal and spatial variations of Southern Ocean diapycnal mixing from Argo profiling floats. Nature Geoscience, 4(6): 363-366 DOI:10.1038/Ngeo1156 |
 2023, Vol. 54
2023, Vol. 54


