
中国海洋湖沼学会主办。
文章信息
- 平洪领, 张涛, 史会来, 付铁中, 林慧, 杨淑越. 2023.
- PING Hong-Ling, ZHANG Tao, SHI Hui-Lai, FU Tie-Zhong, LIN Hui, YANG Shu-Yue. 2023.
- 浙江近海横带髭鲷(Hapalogenys mucronatus)表型性状与体重的通径分析及曲线拟合
- PATH ANALYSIS AND CURVE FITTING OF PHENOTYPIC TRAITS AND BODY WEIGHT OF HAPALOGENYS MUCRONATUS IN ZHEJIANG OFFSHORE
- 海洋与湖沼, 54(4): 1199-1206
- Oceanologia et Limnologia Sinica, 54(4): 1199-1206.
- http://dx.doi.org/10.11693/hyhz20221200329
文章历史
-
收稿日期:2022-12-15
收修改稿日期:2023-02-21
2. 浙江海洋大学海洋与渔业研究所 浙江舟山 316021
2. Zhejiang Ocean University, Zhejiang Marine Fisheries Research Institute, Zhoushan 316021, China
横带髭鲷(Hapalogenys mucronatus)隶属于鲈形目(Perciforms)、石鲈科(Pamadasyidae)、髭鲷属(Hapalogenys), 俗称十六枚。主要生活在多岩礁的海区, 是一种典型的近海岛礁性鱼类, 因具有味道鲜美、营养价值高及艳丽的体色等优点, 深受垂钓爱好者及消费者的青睐。目前关于横带髭鲷的研究主要集中在遗传多样性(王世锋等, 2008; 徐田军等, 2010; Zheng et al, 2020)、细胞遗传学(喻子牛等, 1994)、繁殖生物学(史海东等, 2004; 平洪领等, 2021)、营养品质评价(张涛等, 2020)等方面。然而, 由于其野生资源量匮乏, 无明显的盛渔期, 仅依靠野生资源量无法满足消费市场需求, 导致市场价格居高不下。
振兴种业是保障国家粮食安全的核心要素, 水产种业为渔业绿色高质量发展发挥着重要基础性作用, 水产遗传育种技术创新是水产种业发展的核心要素。截至2022年, 我国培育水产新品种266个, 其中152个为选育品种, 目前仍以群体选育、杂交等传统技术为主(胡红浪等, 2023)。2022年国家审定通过的26个水产新品种中有13个为鱼类新品种, 15个为选育新品种(中国人民共和国农业农村部, 2022)。选择育种技术在水产品种重要经济性状的遗传改良方面发挥着重要作用, 陈松林等(2008)利用选择育种和家系间杂交等技术, 培育了“鲆优1号”, 苗亮等(2014)采用群体选育技术, 培育大黄鱼“东海1号”。在鱼类生长性状的遗传育种过程中, 体重为最常用的遗传改良目标性状(楼允东, 1999)。但是在精确测量活体体重时有一定难度, 由于体表残留的水分、肠道内的饲料残渣和粪便都会对测量结果产生较大影响, 而表型性状则具有易于准确测量的特点。因此, 开展表型性状与体重的相关分析, 通过通径分析的手段, 筛选出影响体重的关键表型性状, 通过表型性状对体重的间接选择, 会获得较理想的选育效果(陈红林等, 2016)。该技术方法已在梭鱼(Liza haematocheila) (耿绪云等, 2011)、三疣梭子蟹(Portunus trituberculatus) (高保全等, 2008)、红鳍东方鲀(Takifugu rubripes) (王新安等, 2013)、真鲷(Pagrus major) (Kora et al, 2000)等水产动物中得到广泛应用。浙江省海洋水产研究所自2017年开展野生横带髭鲷亲鱼驯养及人工繁育研究工作, 已突破人工繁育技术。关于横带髭鲷表型性状与体重之间关系的研究尚未见报道。本研究精准测量了野生横带髭鲷的10个表型性状, 利用相关分析、通径分析、回归分析等方法探究了表型性状对体重的影响, 并建立多元回归方程, 分别以列入回归方程的4个表型性状为自变量, 体重为因变量进行曲线模型拟合, 筛选出最优拟合模型。开展横带髭鲷表型性状与体重的关系研究, 可为今后开展横带髭鲷选择育种和人工养殖工作提供理论指导。
1 材料与方法 1.1 实验材料2021年11月于舟山海域采用拖虾船采集野生横带髭鲷样本, 所采集的样本均为新鲜活体, 使用打包充氧袋运回实验室进行测量工作, 通过鳞片鉴定为同一年龄段的鱼群, 从中随机测量139尾。
1.2 实验方法参考刘贤德等(2008)对大黄鱼(Pseudosciaena crocea)的测量方法, 测量前停食24 h, 使用5 ℃冷水进行冷休克处理, 擦拭鱼体表海水, 用游标卡尺准确测量全长(X1)、体长(X2)、头长(X3)、躯干长(X4)、尾部长(X5)、眼径(X6)、体高(X7)、尾柄高(X8)、体宽(X9)、眼间距(X10)10个表型性状指标, 精确到0.01 mm, 用电子天平准确称量体重(Y), 精确到0.01 g。各表型性状测量方法如图 1所示。
 |
| 图 1 横带髭鲷表型性状测量方法 Fig. 1 Measurement of phenotypic traits of H. mucronatus |
使用SPSS 19.0软件对表型性状和体重数据进行描述性统计分析, 统计各性状的平均值、标准差及变异系数。运用Pearson法对各性状进行相关性分析; 以各表型性状数据为自变量, 体重为因变量, 运用逐步引入-剔除法进行回归分析, 进行表型性状对体重的通径分析, 计算通径系数、间接通径系数、决定系数。
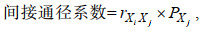 (1)
(1)式中, rXiXj为性状Xi和Xj之间的相关系数, PXj为性状Xj对体重的通径系数。
利用相关系数和通径系数, 计算决定系数:
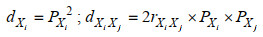 (2)
(2)式中, dXi为性状Xi对体重的决定系数, dXiXj为任意两个表型性状Xi和Xj对体重的共同决定系数, rXiXj为两个表型性状Xi和Xj之间的相关系数, PXi为性状Xi对体重的通径系数, PXj为性状Xj对体重的通径系数。
2 结果与分析 2.1 横带髭鲷表型性状分布特征横带髭鲷所有表型性状和体重数据统计值见表 1。由表 1可见, 体重的变异系数最大, 为32.42%, 而表型性状的变异系数则相对较小, 并且差异不大, 最大值为体宽14.60%, 最小值为眼径8.19%。说明对横带髭鲷来说选择潜力最大的性状是体重, 其次为体宽, 最小的为眼径。
| 参数 | 平均值 | 标准差(SD) | 变异系数(CV)/% |
| 体重/g | 30.56 | 9.91 | 32.42 |
| 全长/cm | 10.94 | 1.21 | 11.05 |
| 体长/cm | 9.11 | 1.00 | 10.98 |
| 头长/cm | 3.31 | 0.35 | 10.53 |
| 躯干长/cm | 2.65 | 0.34 | 12.82 |
| 尾部长/cm | 3.49 | 0.41 | 11.72 |
| 眼径/cm | 0.92 | 0.08 | 8.19 |
| 体高/cm | 4.39 | 0.52 | 11.91 |
| 尾柄高/cm | 0.97 | 0.11 | 11.78 |
| 体宽/cm | 1.68 | 0.25 | 14.60 |
| 眼间距/cm | 0.70 | 0.08 | 11.69 |
从表 2可知, 横带髭鲷各性状之间均呈现极显著正相关(P < 0.01), 从各表型性状之间的相关性来看, 全长与体长的相关系数(0.967)最大; 从表型性状与体重的相关性分析来看, 体高与体重的相关系数(0.958)最大; 从各性状之间的相关性角度来看, 尾柄高与眼径的相关系数(0.674)最小。
| 性状 | 体重 | 全长 | 体长 | 头长 | 躯干长 | 尾部长 | 眼径 | 体高 | 尾柄高 | 体宽 | 眼间距 |
| 体重 | 1 | ||||||||||
| 全长 | 0.936** | 1 | |||||||||
| 体长 | 0.945** | 0.967** | 1 | ||||||||
| 头长 | 0.920** | 0.921** | 0.936** | 1 | |||||||
| 躯干长 | 0.822** | 0.836** | 0.876** | 0.794** | 1 | ||||||
| 尾部长 | 0.881** | 0.907** | 0.918** | 0.870** | 0.739** | 1 | |||||
| 眼径 | 0.756** | 0.754** | 0.783** | 0.787** | 0.700** | 0.704** | 1 | ||||
| 体高 | 0.958** | 0.922** | 0.940** | 0.927** | 0.807** | 0.886** | 0.773** | 1 | |||
| 尾柄高 | 0.908** | 0.888** | 0.892** | 0.873** | 0.777** | 0.818** | 0.674** | 0.908** | 1 | ||
| 体宽 | 0.912** | 0.875** | 0.895** | 0.873** | 0.824** | 0.844** | 0.743** | 0.917** | 0.837** | 1 | |
| 眼间距 | 0.911** | 0.867** | 0.887** | 0.869** | 0.749** | 0.852** | 0.698** | 0.898** | 0.868** | 0.869** | 1 |
| 注: **表示变量之间存在极显著相关性(P < 0.01) | |||||||||||
通径分析结果见表 3。本研究共测量10个表型性状指标, 采用逐步引入-剔除自变量的方法进行回归分析, 剔除掉对体重影响不显著的6个表型性状, 保留了全长、体高、体宽和眼间距4个表型性状, 检验结果表明, 全长、眼间距和体高对体重的直接作用(通径系数)达到极显著水平(P < 0.01), 体宽对体重的直接作用达到显著水平(P < 0.05)。4个表型性状对体重的直接作用均小于间接作用。体高对体重的直接作用最大(通径系数为0.433), 依次为全长(通径系数为0.286)、眼间距(通径系数为0.179)、体宽(通径系数0.110)。从间接作用总和来看, 体宽的间接作用最大, 作用系数为0.803, 体高的间接作用最小(0.526)。
| 变量 | 相关系数 | 直接作用 | 间接作用 | ||||
| 全长 | 体高 | 体宽 | 眼间距 | Σ | |||
| 全长 | 0.936** | 0.286** | 0.399 | 0.096 | 0.155 | 0.650 | |
| 体高 | 0.958** | 0.433** | 0.264 | 0.101 | 0.161 | 0.526 | |
| 体宽 | 0.912** | 0.110* | 0.250 | 0.397 | 0.156 | 0.803 | |
| 眼间距 | 0.911** | 0.179** | 0.248 | 0.389 | 0.096 | 0.733 | |
| 注: *表示显著相关(P < 0.05), **表示极显著相关(P < 0.01) | |||||||
4个表型性状对体重的决定系数见表 4。表 4对角线上4组数字为各性状的直接决定系数, 对角线以上的数字为两个性状的共同决定系数。从4个性状的直接决定系数来看, 体高的直接决定系数(0.187)明显大于其他3个性状, 全长次之(0.082), 体宽最小(0.012)。从4个性状的共同决定系数来看, 全长和体高的共同决定系数最大(0.228), 体宽和眼间距的共同决定系数最小(0.034)。直接决定系数和共同决定系数的总和为0.945, 表明影响横带髭鲷体重的主要表型性状为全长、体高、体宽和眼间距, 其中, 最关键的性状是体高和全长。
| 性状 | 全长 | 体高 | 体宽 | 眼间距 | Σ |
| 全长 | 0.082 | 0.228 | 0.055 | 0.089 | 0.454 |
| 体高 | 0.187 | 0.087 | 0.139 | 0.413 | |
| 体宽 | 0.012 | 0.034 | 0.046 | ||
| 眼间距 | 0.032 | 0.032 | |||
| Σ | 0.082 | 0.415 | 0.154 | 0.294 | 0.945 |
使用逐步线性回归法, 以全长(X1)、体高(X7)、体宽(X9)和眼间距(X10) 4个表型性状为自变量, 体重为因变量建立多元回归方程。
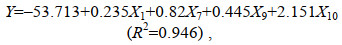 (3)
(3)式中, Y表示体重, X1、X7、X9、X10分别表示全长、体高、体宽和眼间距。
由表 5可知, 随着4个自变量的逐步带入, 回归方程相关系数由0.958逐步增大到0.973, 说明引入的自变量对体重的作用在增加, 说明构建的回归方程具有较好的参考价值。由表 6的回归系数分析结果可知, 体高和全长对体重的决定作用较大, 体宽和眼间距次之。利用回归方程的相关系数可以计算出剩余因子e, 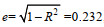
| 模型 | R | R2 | 调整后R2 | 标准估计的误差 |
| 1 | 0.958 | 0.918 | 0.917 | 2.850 27 |
| 2 | 0.968 | 0.937 | 0.936 | 2.512 77 |
| 3 | 0.972 | 0.944 | 0.943 | 2.370 47 |
| 4 | 0.973 | 0.946 | 0.944 | 2.341 38 |
| 模型 | 偏回归系数 | 回归系数 | t | P | ||
| B | 标准误差(SE) | |||||
| 1 | 常量 | –49.144 | 2.052 | –23.952 | 0.000 | |
| 体高 | 1.815 | 0.046 | 0.958 | 39.118 | 0.000 | |
| 2 | 常量 | –53.734 | 1.948 | –27.583 | 0.000 | |
| 体高 | 1.197 | 0.106 | 0.632 | 11.326 | 0.000 | |
| 全长 | 0.290 | 0.046 | 0.354 | 6.346 | 0.000 | |
| 3 | 常量 | –55.066 | 1.865 | –29.531 | 0.000 | |
| 体高 | 0.946 | 0.116 | 0.499 | 8.141 | 0.000 | |
| 全长 | 0.248 | 0.044 | 0.302 | 5.586 | 0.000 | |
| 眼间距 | 2.422 | 0.574 | 0.201 | 4.221 | 0.000 | |
| 4 | 常量 | –53.713 | 1.952 | –27.517 | 0.000 | |
| 体高 | 0.820 | 0.129 | 0.433 | 6.336 | 0.000 | |
| 全长 | 0.235 | 0.044 | 0.286 | 5.308 | 0.000 | |
| 眼间距 | 2.151 | 0.581 | 0.179 | 3.701 | 0.000 | |
| 体宽 | 0.445 | 0.213 | 0.110 | 2.092 | 0.038 | |
通过通径分析和回归分析结果, 分别以剔除后的4个表型性状全长(X1)、体高(X7)、体宽(X9)和眼间距(X10)为自变量, 拟合与因变量体重(Y)的最佳方程模型。由表 7列出的5种方程的拟合结果可知, 横带髭鲷全长(X1)与体重(Y)的最佳拟合模型为幂函数, 拟合方程式为Y=1.484⊆10–5X13.088 (R2=0.920), 体高(X7)与体重(Y)的最佳拟合模型为S函数, 拟合方程式为Y=e-111.504/X7(R2=0.952), 体宽(X9)与体重的最佳拟合模型为S函数, 拟合方程式为Y=e-27.976/X9 (R2=0.884), 眼间距(X10)与体重的最佳拟合模型为S函数, Y= e-13.242/X10(R2=0.850), 拟合模型图见图 2。
| 回归 | 模型 | 模型汇总 | 参数估计值 | ||||
| R2 | F | P | 常数 | 系数b1 | |||
| X1-Y | 线性 | 0.877 | 975.015 | 0.000 | –53.412 | 0.768 | |
| 对数 | 0.842 | 730.024 | 0.000 | –334.676 | 77.906 | ||
| 幂 | 0.920 | 1 586.023 | 0.000 | 1.484×10–5 | 3.088 | ||
| S | 0.918 | 1 527.710 | 0.000 | 6.218 | –308.486 | ||
| 指数 | 0.901 | 1 251.783 | 0.000 | 1.140 | 0.030 | ||
| X7-Y | 线性 | 0.918 | 1 530.196 | 0.000 | –49.144 | 1.815 | |
| 对数 | 0.884 | 1 044.174 | 0.000 | –249.756 | 74.266 | ||
| 幂 | 0.950 | 2 604.262 | 0.000 | 0.001 | 2.919 | ||
| S | 0.952 | 2 688.337 | 0.000 | 6.079 | –117.583 | ||
| 指数 | 0.926 | 1 725.462 | 0.000 | 1.381 | 0.069 | ||
| X9-Y | 线性 | 0.832 | 679.421 | 0.000 | –31.353 | 3.688 | |
| 对数 | 0.800 | 546.368 | 0.000 | –128.017 | 56.451 | ||
| 幂 | 0.883 | 1 034.104 | 0.000 | 0.052 | 2.249 | ||
| S | 0.884 | 1 035.275 | 0.000 | 5.389 | –33.265 | ||
| 指数 | 0.852 | 791.249 | 0.000 | 2.672 | 0.141 | ||
| X10-Y | 线性 | 0.830 | 670.575 | 0.000 | –46.647 | 10.971 | |
| 对数 | 0.818 | 613.903 | 0.000 | –115.106 | 74.921 | ||
| 幂 | 0.832 | 677.949 | 0.000 | 0.109 | 2.865 | ||
| S | 0.850 | 775.706 | 0.000 | 6.154 | –19.396 | ||
| 指数 | 0.800 | 547.615 | 0.000 | 1.625 | 0.408 | ||
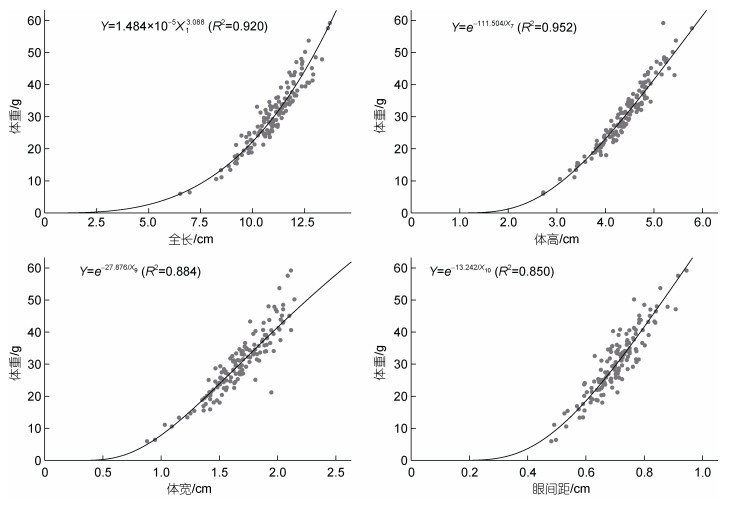 |
| 图 2 横带髭鲷4个表型性状的最佳拟合模型图 Fig. 2 The best-fitting model of four phenotypic traits of H. mucronatus |
目前, 大多数通过审定的水产新品种都将生长速度或体重作为目标性状(中国人民共和国农业农村部, 2021), 在选择育种中, 生长性状的主要评价指标为体重。一般认为变异系数越大的性状, 其遗传育种的潜力越大, 更适合作为选育的目标性状(李艳慧等, 2022)。本研究中, 通过精确测定横带髭鲷的11个性状中, 体重的变异系数最大(32.42%), 表型性状中变异系数最大的为体宽(14.60%), 体重明显大于10个表型性状的变异系数, 而10个表型性状之间的变异系数差异不大。该研究结果与小黄鱼(刘峰等, 2016)、野生叶尔羌高原鳅(李艳慧等, 2022)、星康吉鳗(张新明等, 2020)、牙鲆(陈红林等, 2016)的研究结果一致, 更加证明将体重作为选育目标性状的科学性。本研究中139尾横带髭鲷为同年龄段鱼群, 且体重数据符合正态分布特征。这说明体重最适合作为横带髭鲷选育目标性状, 该研究结果为指导横带髭鲷的育种工作具有现实意义。
3.2 影响横带髭鲷体重的主要表型性状许多研究表明, 水产动物自身的表型性状与体重之间具有较显著的相关性(王新安等, 2013; 刘峰等, 2016; 李艳慧等, 2022), 可以通过选择较易准确测量的表型性状指标间接达到选育体重目标性状的目的。本研究中, 横带髭鲷各表型性状与体重均呈现极显著正相关(P < 0.01), 说明横带髭鲷体重变化与各表型性状之间存在相互联系和相互制约的关系, 但这种关系又是一种无法完全确定的函数关系, 相关分析只能获得表型性状与体重的简单相关关系。同时, 较强的相关性也会导致信息的叠加, 表现为表型性状与体重之间存在多重共线性问题, 单从相关性分析还无法区分出对体重起到关键作用的表型性状。通径分析和回归分析可分析多个自变量与因变量的多重共线性关系, 将复杂的变量相互关系简化。通径分析可以获得各自变量的直接作用和间接作用, 再通过计算决定系数和回归分析结果, 可以确定影响因变量变化的主要自变量(李艳慧等, 2022)。本研究通径分析结果表明, 仅有全长、体高、体宽和眼间距4个表型性状与体重之间的通径系数达到显著水平(P < 0.05), 而其他6个表型性状则被剔除, 由表 3的通径分析发现体高对体重的直接作用最大(0.433), 大小依次为全长(0.286)、眼间距(0.179)、体宽(0.110)。体高、全长和眼间距与体重的通径系数均达到极显著水平(P < 0.01), 仅体宽为显著水平(P < 0.05), 同时, 体宽对体重的直接作用也最小, 而体宽的间接作用却最大, 通过全长、体高和眼间距间接作用总和为0.803。说明横带髭鲷体高、全长和眼间距直接影响体重变化, 而体宽对体重变化的影响则通过体高、全长和眼间距间接作用。
本研究中决定系数计算结果见表 4可知, 体高、全长、眼间距和体宽4个表型性状对体重的决定系数总和为0.945, 表明这4个表型性状是影响横带髭鲷体重的主要性状。体高的直接决定系数最大(0.187), 大小依次为全长(0.082)、眼间距(0.032)和体宽(0.012), 全长和体高的共同决定系数最大(0.228)。这与通径分析的结果一致。通径分析和决定系数计算结果均表明体高和全长是影响体重变化的最为主要的表型性状, 该结果与横带髭鲷外形特征相吻合, 体侧扁而高, 呈长椭圆形, 体高描述了横带髭鲷体形横向生长的特征, 全长描述了纵向特征。具有相同体形特征的斜带髭鲷(萧云朴等, 2013)、黑鲷(王雪等, 2019)、回交鲷(刘海林等, 2018)、条石鲷(黄伟卿等, 2015)研究具有相同结果。通过构建多元回归方程计算出剩余因子e, e=0.232, 说明除了被选出的4个表型性状对横带髭鲷体重变化有较大影响外, 还有一些会对体重变化产生影响的性状未考虑到, 还需要进一步研究。
3.3 拟合模型的筛选在实际生产中, 自变量和因变量之间的相关关系, 并非一定是线性关系, 更多情况下是曲线关系。在水产育种工作中, 常用简单易测的表型性状预测体重的变化规律, 通过拟合表型性状与体重的曲线模型, 以提高育种效率和准确度(刘莹等, 2018; 李艳慧等, 2022)。本研究中分别拟合了4个主要表型性状与体重的曲线模型, 拟合结果表明4个表型性状与体重拟合曲线模型的F检验P值远小于0.01, 说明模型成立的统计学意义均非常显著, 拟合模型有效。拟合度R2表示曲线模型估测的可靠程度, 由表 7可以看出, 4个表型性状与体重的最优拟合曲线模型的R2均大于0.85, 说明全长、体高、眼间距和体宽均可较好地反映体重变化规律, 特别是全长和体高分别与体重的拟合度R2较大, 这与通径分析和决定系数计算结果一致, 再次证明全长和体高是最主要影响体重变化的性状。从4个最佳拟合模型的类型来看, 除了全长与体重的拟合模型为幂函数模型外, 其他3个模型均为S函数模型。S函数模型又称生长曲线模型, 说明所选择的表型性状很好地反映了横带髭鲷的生长过程, 预测生长规律。陈红林等(2016)对不同生长期的牙鲆研究表明幼鱼期和成鱼期的生长模式不同, 适用模型也不同, 需要对不同生长阶段的牙鲆建立最优模型, 有利于提高选择育种工作。刘莹等(2018)对不同生长期的大菱鲆研究也表明大菱鲆的生长模式会随鱼体生长而变化。因此, 本研究下一步需要持续探究不同生长阶段的横带髭鲷表型性状与体重的最佳拟合模型情况, 为横带髭鲷的选育工作提供更加精准的理论数据。
4 结论本研究进行通径分析、多元回归分析和曲线拟合, 系统揭示了横带髭鲷各表型性状与体重的关系。研究表明, 通径分析和决定系数计算结果均表明体高和全长是影响体重变化的最为主要的表型性状, 该结果与横带髭鲷外形特征相吻合, 体侧扁而高, 呈长椭圆形, 体高描述了横带髭鲷体形横向生长的特征, 全长描述了纵向特征。在以横带髭鲷体重为育种目标性状时, 可以全长和体高为主要选育性状, 而眼间距和体宽则为辅助性状。这为今后开展横带髭鲷育种工作提供重要的理论依据。
王世锋, 杜佳莹, 苏永全, 等, 2008. 厦门近海横带髭鲷野生群体遗传结构分析. 厦门大学学报(自然科学版), 47(1): 88-93 |
王雪, 李莉, 刘元文, 等, 2019. 3月龄黑鲷形态性状对体质量的影响效果分析. 大连海洋大学学报, 34(2): 233-238 |
王新安, 马爱军, 庄志猛, 等, 2013. 红鳍东方鲀(Takifugu rubripes)形态性状对体重的影响效果. 海洋与湖沼, 44(1): 135-140 |
中国人民共和国农业农村部, 2021. 中华人民共和国农业农村部公告第451号[EB/OL]. (2021-08-02)[2022-07-23].
|
中华人民共和国农业农村部, 2022. 中华人民共和国农业农村部公告第578号[EB/OL]. (2022-07-14)[2022-07-20].
|
平洪领, 张涛, 史会来, 等, 2021. 横带髭鲷早期生长发育特征. 中国水产科学, 28(3): 276-287 |
史海东, 毛国民, 王海岳, 2004. 温度和盐度对横带髭鲷胚胎发育的影响. 上海水产大学学报, 13(3): 230-234 |
刘贤德, 蔡明夷, 王志勇, 等, 2008. 闽-粤东族大黄鱼生长性状的相关与通径分析. 中国海洋大学学报, 38(6): 916-920 |
刘莹, 于超勇, 于道德, 等, 2018. 不同生长时期大菱鲆(Scophthalmus maximus)形态性状与体质量的通径分析及曲线拟合研究. 广西科学院学报, 34(3): 181-190 |
刘峰, 陈琳, 楼宝, 等, 2016. 小黄鱼(Pseudosciaena polyactis)形态性状与体质量的相关性及通径分析. 海洋与湖沼, 47(3): 655-662 |
刘海林, 祝斐, 张志勇, 等, 2018. 18月龄回交鲷生长性状的相关分析与通径分析. 江苏农业科学, 46(21): 183-185, 195 |
李艳慧, 陈生熬, 程勇, 2022. 叶尔羌高原鳅形态性状与体重的通径分析及曲线拟合. 中国水产科学, 29(1): 49-57 |
张涛, 平洪领, 史会来, 等, 2020. 舟山海域不同规格横带髭鲷营养成分分析及品质评价. 浙江海洋大学学报(自然科学版), 39(6): 502-508 |
张新明, 程顺峰, 2020. 星康吉鳗形态性状与体重的通径分析及生长曲线拟合. 中国水产科学, 27(10): 1167-1175 |
陈红林, 田永胜, 刘峰, 等, 2016. 不同时期牙鲆形态性状对体重影响的通径分析及曲线拟合研究. 中国水产科学, 23(1): 64-76 |
陈松林, 田永胜, 徐田军, 等, 2008. 牙鲆抗病群体和家系的建立及其生长和抗病性能初步测定. 水产学报, 32(5): 665-673 |
苗亮, 李明云, 陈炯, 等, 2014. 快长、耐低温大黄鱼新品种东海1号的选育. 农业生物技术学报, 22(10): 1314-1320 |
胡红浪, 韩枫, 桂建芳, 2023. 中国水产种业技术创新现状与展望. 水产学报, 47(1): 019101 |
耿绪云, 马维林, 李相普, 等, 2011. 梭鱼(Liza haematocheila)外部形态性状对体重影响效果分析. 海洋与湖沼, 42(4): 530-537 |
徐田军, 王健鑫, 孙悦娜, 等, 2010. 基于髭鲷属鱼类Cyt b基因全序列探讨髭鲷属在鲈总科的分类地位. 动物分类学报, 35(3): 530-536 |
高保全, 刘萍, 李健, 等, 2008. 三疣梭子蟹形态性状对体重影响的分析. 海洋水产研究, 29(1): 44-50 |
黄伟卿, 周瑞发, 谢友亮, 等, 2015. 4月龄条石鲷形态性状对体质量的影响效果分析. 水产科学, 34(8): 515-518 |
萧云朴, 吴加将, 杨传爱, 等, 2013. 2种规格斜带髭鲷形态性状对体质量影响的相关分析. 现代农业科技, (1): 242-244, 248 |
喻子牛, 孔晓瑜, 徐文武, 等, 1994. 斜带髭鲷Hapalogenys nitens (Richardson)和横带髭鲷H. mucronatus (Eydoux et Souleyet)的核型. 青岛海洋大学学报, 24(2): 175-180 |
楼允东, 1999. 鱼类育种学. 北京: 中国农业出版社, 3-5
|
KORA H, TSUCHIMOTO M, MIYATA K, et al, 2000. Estimation of body fat content from standard body length and body weight on cultured red sea bream. Fisheries Science, 66(2): 365-371 |
ZHENG Y Y, FENG L X, LIU H Y, et al, 2020. The complete mitochondrial genome of Hapalogenys analis (Perciformes, Haemulidea) except for control region, obtained by whole genome sequencing. Mitochondrial DNA Part B, 5(3): 2807-2808 |
 2023, Vol. 54
2023, Vol. 54


