
中国海洋湖沼学会主办。
文章信息
- 田静, 张凡, 李任之, 高超, 吴昊, 邢飞, 高建华, 汪亚平. 2023.
- TIAN Jing, ZHANG Fan, LI Ren-Zhi, GAO Chao, WU Hao, XING Fei, GAO Jian-Hua, WANG Ya-Ping. 2023.
- 长江口湍流剖面的观测与分析
- OBSERVATION AND ANALYSIS OF TURBULENCE VERTICAL PROFILE IN THE CHANGJIANG RIVER ESTUARY
- 海洋与湖沼, 54(5): 1295-1307
- Oceanologia et Limnologia Sinica, 54(5): 1295-1307.
- http://dx.doi.org/10.11693/hyhz20230200023
文章历史
-
收稿日期:2023-02-03
收修改稿日期:2023-03-10
2. 华东师范大学河口海岸学国家重点实验室 上海 200241
2. State Key Laboratory of Estuarine and Coastal Research, East China Normal University, Shanghai 200241, China
湍流通常被认为是一种高能旋转的涡流运动状态, 其引起的混合速率远高于单独的分子扩散过程(Thorpe, 2007)。在河口系统中, 湍流混合是控制物质(如沉积物、污染物质、营养盐等)及能量(如动量、热量等)交换的重要物理过程, 对河口沉积、地貌演化、生物化学过程等有着重要的影响(Bakhoday-Paskyabi et al, 2018)。湍流混合相关的特征参数包括摩阻流速、拖曳系数、湍动能、湍动能剪切生成、湍动能耗散率、浮力通量等。其中, 摩阻流速和拖曳系数是描述底边界层流体特性的重要参数(Soulsby et al, 1981), 其准确性是影响河口水动力数值模型精度的主要因素(Davies et al, 1994; Guo et al, 1998)。而湍动能剪切生成、湍动能耗散率、浮力通量等则是湍流能量平衡的主控因子(Trowbridge et al, 1999; Rippeth et al, 2001)。近年来关于湍流能量平衡的研究显示, 河口海岸浅水区中的湍流能量大多处于非局地平衡状态, 即在忽略湍动能时空变化的前提下, 湍动能剪切生成无法与湍动能耗散率、浮力通量相平衡。Talke等(2013)在斯诺霍米什河口的观测中发现, 近底部摩擦是湍动能的源, 该处产生的湍动能向上运输, 导致近底部湍动能剪切生成远超过湍动能耗散率与浮力通量之和。随着距底距离的增加, 湍动能的垂向扩散使得湍动能剪切生成小于湍动能耗散率与浮力通量之和。Li等(2022)利用安装在底层的声学多普勒点式流速仪(acoustic doppler velocimeters, ADV)对长江口进行湍流观测, 发现底层水体在涨潮期间出现了湍流局地平衡, 落潮期间则呈现出湍动能耗散率远大于湍动能剪切生成的现象, 并把这种现象归因于湍动能对流项的影响。林姚坤等(2018)在长江口的观测显示, 受水体层化的影响, 水体的能量关系仅在水体底部混合层内符合湍动能局地平衡。Wang等(2015)通过对梅里马克河口的多年观测发现, 羽流虽然会造成河口水体的分层, 但也会产生强剪切并形成强的湍流, 且强剪切效应对湍流发育的影响更加明显。因此, 河口海岸地区的湍流能量受垂向扩散、水平对流、水体层化等多种因素的影响, 从而呈现出复杂的特征。湍流结构和能量转换过程的研究对认识河口物质混合、构建海洋模型有重要意义。
河口湍流研究主要依赖于高分辨率高频现场观测。声学多普勒点式流速仪ADV由于具有高频的突出优点, 被广泛应用于河口湍流观测中(Voulgaris et al, 1998)。但由于其只能进行单点观测, 因此很难获取完整水柱的高质量湍流剖面资料。传统声学多普勒海流剖面仪ADCP虽然可以获取高频流速剖面数据, 但由于受采样频率限制, 其声学信号噪音较大, 致使湍流信号被噪音覆盖。此外, ADCP的垂向流速是通过多个波束合成得到的, 其水平流速对湍流信号的影响难以被完全摒除(Stacey et al, 1999)。同时, 在水深较浅的河口海岸区域, 微结构剖面仪等主流湍流剖面观测仪器的使用受限, 无法进行高密度的长期观测(刘志宇, 2009)11。Nortek公司新近推出的新型5波束Signature 1000kHz AD2CP具有宽带、高频、低噪等特点, 且其第5波束可直接观测垂向流速, 由此可以直接计算雷诺应力、湍动能等湍流特征参数, 显著优化了四波束方差法(Guerra et al, 2017)。
长江是世界第三大河, 其河口地区的水动力结构受到河流冲淡水、风力驱动的陆架环流、潮流、波浪以及人类活动等多种过程的共同控制(沈焕庭等, 1999; 时钟, 2001), 湍流效应显著(熊龙兵, 2014)。受限于观测技术、仪器精度以及水深等多重因素, 长江口近海区域的湍流剖面资料十分匮乏, 人们对长江口水体的湍流结构知之甚少。为此, 本文尝试在长江口近海海域投放座底式三角架, 采用AD2CP和ADV进行同步观测, 获取长江口湍流剖面结构特征, 为深入开展长江口物质混合研究和模型开发等提供关键资料。
1 材料与方法 1.1 现场观测为减少径流的影响, 本文选择枯季在长江口不同水深区域的两个站位进行现场观测(图 1a与图 1b)。T1站位(122°00.690′E, 31°06.553′N)位于长江口南槽拦门沙海域, 平均水深8.2 m, 观测时间段为2019年1月12日18:00至1月16日22:00; T2站位(122°57.110′E, 30°56.379′N)位于长江水下三角洲前缘, 平均水深44.7 m, 观测时间为2019年12月10日14:00至12月16日20:00。
观测期间, ADV和光学后向散射浊度计(optical backscatter point sensor, OBS)固定于座底式三脚架上, ADV采样方式为Burst模式, 每10 min以16 Hz的采样频率测量高频流速512 s; OBS采样频率为1 Hz, 采样周期为5 min, 连续测20 s (图 1c)。新型5波束声学多普勒流速剖面仪(Nortek Signature 1 000 kHz AD2CP)被固定于另外一个相近的座底式四脚架上进行仰视观测(图 1d), 采样方式为Burst模式, 每20 min以8 Hz的采样频率测量高频流速512 s (表 1)。同时, 在距离海底三脚架约200 m处布置WatchKeeper Buoy型波浪浮标(加拿大AXYS公司生产)以直接获得每小时的波浪数据。此外, 将一台温盐深仪Seabird19+CTD和一台OBS安装于船载观测架中, 利用绞车每1~2 h进行垂向剖面观测, 以获取海水的温度、盐度、浊度剖面数据, 同时每小时进行底、中、表三层现场水样采集。
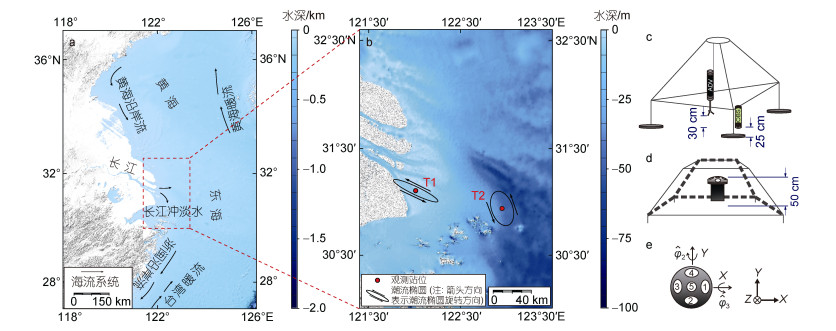 |
图 1 研究区域(a)、观测站位(b)、现场仪器安装示意图(c和d)以及AD2CP俯视图(e) Fig. 1 The study area (a), the location of observation stations (b), schematic diagram of field instrument installation (c, d) and top view of the AD2CP (e) 注: c: 座底式三脚架及声学多普勒点式流速仪(acoustic doppler velocimeters, ADV)、光学后向散射浊度计(optical backscatter point sensor, OBS)安装示意图; d: 座底四脚架及新型5波束声学多普勒流速剖面仪(Nortek Signature 1 000 kHz AD2CP)安装示意图; e: 根据Janus配置, 笛卡尔(XYZ)坐标系下AD2CP波束、倾角(纵摇及横摇)示意图, 其中1~5代表AD2CP第1~5波束, 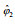 代表AD2CP的纵摇, 代表AD2CP的纵摇,  代表AD2CP的横摇, 因AD2CP与传统ADCP的平摇( 代表AD2CP的横摇, 因AD2CP与传统ADCP的平摇(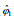 )命名方式无差别, 故在此不作展示 )命名方式无差别, 故在此不作展示 |
| 站位 | 仪器 | 距底高度/m | 盲区/m | 层厚/m | 采样频率/Hz | 采样个数/个 | 采样间隔/min | 采样时间/s |
| T1 | AD2CP | 0.5 | 0.5 | 1 | 8 | 4 096 | 20 | 512 |
| ADV | 0.3 | – | – | 16 | 8 192 | 10 | 512 | |
| OBS | 0.25 | – | – | 1 | 20 | 5 | 20 | |
| T2 | AD2CP | 0.5 | 0.1 | 2 | 8 | 4 096 | 20 | 512 |
| ADV1 | 0.4 | – | – | 16 | 8 192 | 10 | 512 | |
| ADV2 | 0.9 | – | – | 16 | 8 192 | 10 | 512 | |
| 注: “–”表示该仪器不具有某一参数 | ||||||||
AD2CP与ADV测量时易受到环境因素的干扰(如大颗粒悬浮物、水体气泡、边界回声等因素), 现场观测数据中会存在不同程度的噪声信息, 因此需要通过相空间阈值法对原始Beam坐标系下的高频流速数据进行预处理, 以获取精确湍流脉动数据(鲁远征等, 2012)。
随后, 将高频流速数据转换变为地球坐标系(east-north-up, ENU)。然后进行经验正交分解以获得主流向、次流向的高频流速数据, 包含平均流速、波浪脉动流速以及湍流脉动流速, 即
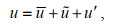 (1)
(1)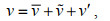 (2)
(2)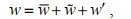 (3)
(3)其中, u、v、w分别为主流向、次流向以及垂向瞬时流速(单位: m/s); 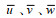
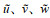
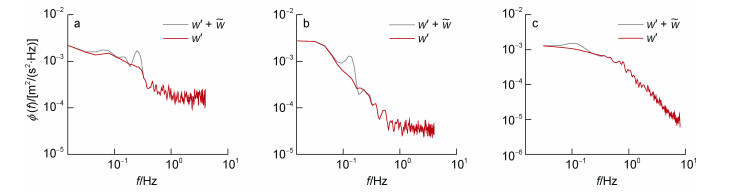 |
图 2 剔除波浪前后的湍流频率能谱密度ϕ(f)举例 Fig. 2 Examples of wave-turbulence spectral decomposition 注: a: T1站位1 m层厚AD2CP (2019年1月13日15:20:00); b: T2站位2 m层厚AD2CP (2019年12月12日20:40:00); c: T1站位ADV (2019年1月13日02:20:00); f为频率(单位: Hz), ϕ(f)与f的计算步骤详见本文1.5章节; 灰色曲线代表剔除波浪前的湍流频率能谱密度W' + 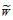 , 红色曲线代表剔除波浪后的湍流频率能谱密度W′ , 红色曲线代表剔除波浪后的湍流频率能谱密度W′ |
由于AD2CP固定在海底, 其倾角值较小, 可采用Dewey等(2007)的优化四波束方差法计算雷诺应力:
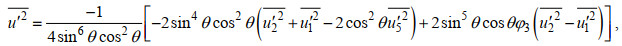 (4)
(4)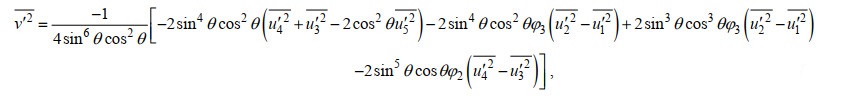 (5)
(5)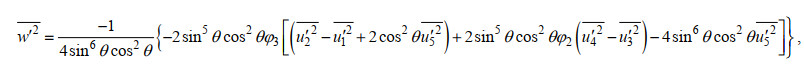 (6)
(6)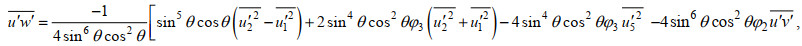 (7)
(7)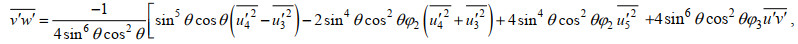 (8)
(8)其中, θ为AD2CP波束的倾角, 为25°; 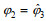
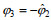
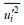
采用现场水样的悬沙浓度来标定OBS的浊度数据Tur (单位: NTU), 结果见图 3a和图 3b。
ADV和AD2CP除了能够测量高频流速, 其记录的回声强度还能反映悬浮沉积物后向散射强度。ADV的回声强度与悬浮沉积物浓度之间的关系如下(Voulgaris et al, 2004)1664:
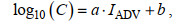 (9)
(9)其中, IADV为ADV测得的回声强度; C为悬沙浓度(单位: mg/L); a、b为回声强度与悬沙浓度之间通过线性回归拟合得到的斜率和截距。基于AD2CP的声学剖面信号反演悬沙浓度的方法与ADV类似, 但需要对沿声波波束路径上的信号衰减进行修正(汪亚平等, 1999)。声波在水体中的衰减机制主要包括声波传输损失、散射损失和水体吸收损失(Urick, 1983; Thorne et al, 1991), 因此引入“范围归一化”回声强度(E)的概念(Lohrmann, 2001):
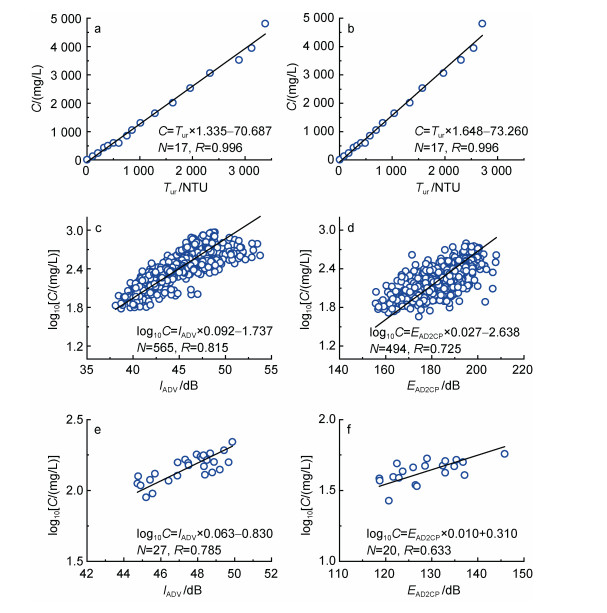 |
| 图 3 悬沙浓度与各站位仪器标定曲线 Fig. 3 Suspended sediment concentration calibration curves 注: a和b为T1站位船载和座底三脚架OBS; c和d为T1站位ADV和AD2CP; e和f为T2站位ADV和AD2CP; C为悬沙浓度(单位: mg/L); Tur为OBS浊度数据(单位: NTU); IADV为ADV测得的回声强度(单位: dB); EAD2CP为AD2CP“范围归一化”回声强度(单位: dB); M为采样个数; R为相关系数 |
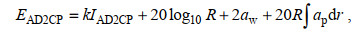 (10)
(10)其中, IAD2CP为AD2CP测得的回声强度; k为IAD2CP的转化系数, 取2.3; R为波束的范围(单位: m); aw为水体吸收系数, Signature 1 000 kHz AD2CP所对应的aw= 0.263 dB/m; ap为颗粒衰减系数, 本文暂时忽略不计。波束范围R的计算公式如下:
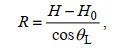 (11)
(11)其中, H为仪器探头距水面距离(单位: m); H0为测量水体距水面距离(单位: m); θL为波束倾角, 对于AD2CP倾斜波束(即第1~4波束)而言, θL= 25 °; 对于垂向波束(即第5波束)而言, θL= 0 °。ADV与AD2CP利用回声强度反演悬沙浓度的结果见图 3c~3f。
1.4 水体层化指标河口水体温度、盐度或者悬浮沉积物不均匀混合会产生垂向密度梯度从而引发层化效应(Simpson et al, 1990)。通常用无量纲的Richardson数Ri来表征水体的层化程度, 具体计算为势能与动能的比值(Turner et al, 1974):
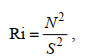 (12)
(12)其中, 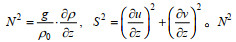
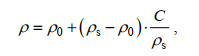 (13)
(13)其中, ρs为沉积物密度, 其值取2 650 kg/m3。
1.5 湍流特征参数采用雷诺应力法确定摩阻流速, 表达式为:
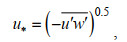 (14)
(14)其中, u*为摩阻流速(单位: m/s); 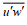
底拖曳系数Cd的表达式为(Green et al, 1995):
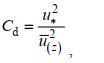 (15)
(15)其中, 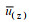
Mestayer等(1978)认为在湍能谱惯性副区内, 湍能谱密度仅与湍动能耗散率ε(单位: m2/s3)、波数k (单位: 1/m)有关, 且边界层内垂向流速比水平流速受波动影响更小:
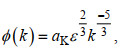 (16)
(16)其中, aK为Kolmogorov普适常数, 其值取0.71; ϕ(k)为湍流波数谱密度(单位: m3/s2)。通过快速傅里叶变化(fast Fourier transformation, FFT), 可将ADV与AD2CP所测的流速数据转变为频率信号, 实现时域与频域的转换(Green, 1992)。结合“Taylor冰冻假设”将仪器实测的湍流频率谱转换为波数谱(Sherwood et al, 2006):
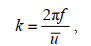 (17)
(17)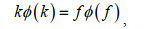 (18)
(18)其中, 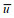
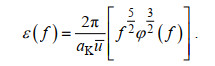 (19)
(19)湍动能剪切生成P (单位: m2/s3)表达式为:
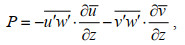 (20)
(20)其中, 雷诺应力项(即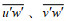
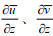
假定每个采样间隔期间水体温度、盐度基本不变, 水体密度变化仅由悬沙浓度变化引起(由ADV、AD2CP反演获得高频悬沙浓度), 可计算出浮力通量B (湍流垂向混合转化的势能, 单位: m2/s3):
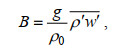 (21)
(21)其中, ρ' 为由悬沙浓度变化引起的水体高频密度波动(单位: kg/m3)。
2 结果 2.1 水动力时空特征观测期间, T1站位(平均水深8.2 m)有效波高为0.15~0.45 m, 处于弱波浪环境(图 4a)。受局部地形影响, T1站位表现为往复流的特征, 涨、落潮平均流向分别为305°、125°, 平均历时分别约为5.6、6.9 h, 最大流速分别为1.74、1.26 m/s (图 4b和图 4c)。在涨、落潮转流时刻, 底层水体的潮流转向比上层水体提前约1~2 h。水体温度在7.9~8.7 ℃之间, 由于冬季海面气温低, 水体呈现一定程度的逆温现象(图 4d)。受径流影响, 水体盐度为2.2~17.8 (图 4e), 最高值出现于落急时刻的中下层水体, 最低值出现于落憩、初涨时刻的表层水体。涨潮时, 高盐度水体由底层入侵, 导致水层盐度升高的时刻由底及表产生了显著相位滞后。水体密度受温度、盐度以及悬沙浓度的影响, 处于1 001.5~1 014.0 kg/m3范围内(图 4f)。水体悬沙浓度为41~781 mg/L, 其中近底层水体悬沙浓度较高(图 4g)。
观测期间, T2站位(平均水深44.7 m)有效波高为0.29~2.34 m, 11日15:00至12日16:00间波浪显著增强, 最大有效波高达2.34 m (图 4k)。潮流为旋转流, 涨、落潮平均流向分别为344°、164°, 平均历时分别约为6.0、6.5 h。T2站位距入海口较远, 受径流影响作用较弱, 涨、落潮最大流速分别为0.92、0.93 m/s (图 4l和图 4m。由于受AD2CP仪器自身观测范围的限制, 有效数据范围仅能覆盖T2站位中下层水体), 温度为14.2~18.2 ℃ (图 4n), 盐度为30.6~33.2 (图 4o), 密度为1 022.4~1 024 kg/m3 (图 4p), 悬沙浓度相对较低, 为37~277 mg/L (图 4q)。
浮力频率N为度量水体垂向自由振动频率的物理量, 用于表征层化水体的稳定性。T1站位N2处于1.3×10−7~4.5×10−2 s−2范围, 其低值大多位于底层水体, 而高值多出现于中上层水体, 水体层化、稳定性较强(图 4h)。水体流速剪切平方S2呈现较为显著潮周期变化, 且由底及表呈现相位滞后现象(图 4i)。由于受到海底摩擦效应的影响, 底层水体流速剪切平方S2一直处于较高水平。根据层状剪切流动的线性理论, 当Ri > 0.25时, 水体流速剪切作用强, 促使湍流发育; 当Ri < 0.25时, 水体层化结构稳定性较强, 抑制湍流发育(Zhang et al, 2018)。如图 4j所示, 水体除了底层混合相对均匀外, 基本处于强层化状态(图中黑线为Ri=0.25的分界线, 下同)。T2站位N2为2.2×10−6~ 2.4×10−3 s−2 (图 4r), S2为1.2×10−4~6.1×10−3 s−2 (图 4s); 距底10 m以下水体混合均匀, 以上水体层化较强(图 4t)。
摩阻流速u*可反映近底边界层水体切应力的大小, 是影响湍流混合的主要因素。T1站位摩阻流速在潮周期内出现两次峰、谷值, ADV与AD2CP所测摩阻流速平均值分别为1.3×10−2 m/s和8.3×10−3 m/s, 其变化趋势与底部流速相位基本一致(图 5a和图 5b), 与之相关的拖曳系数Cd平均值分别为2.9×10−3与1.4×10−3 (图 5c)。T2站位ADV1、ADV2与AD2CP所测摩阻流速平均值分别为1.6×10−2、1.2×10−2、8.0×10−3 m/s (图 5e), 与之相应的拖曳系数平均值为3.2×10−3、1.9×10−3和5.0×10−4 (图 5f)。数据分析结果显示, ADV和AD2CP计算的结果较为吻合, 且T1站位拖曳系数与前人在南槽的观测结果数量级基本一致(汪亚平等, 2006; 兰庭飞等, 2019)。
 |
| 图 4 T1 (a~j)和T2 (k~t)站位的有效波高、主流向流速、次流向流速、温度、盐度、密度、悬沙浓度、浮力频率N2、流速剪切S2以及理查森数Ri剖面图 Fig. 4 The vertical profiles of significant wave height, velocity along the major-axis, velocity along the minor-axis, temperature, salinity, water density, suspended sediment concentration, buoyancy frequency N2, the square vertical shear S2, and Richardson number Ri at T1 (a~j) station and T2 (k~t) station, respectively 注: k中黄色阴影部分为强波浪时刻; a ~t彩色等值线上方的黑色波浪线代表水位曲线, 水位上升代表涨潮, 反之代表落潮 |
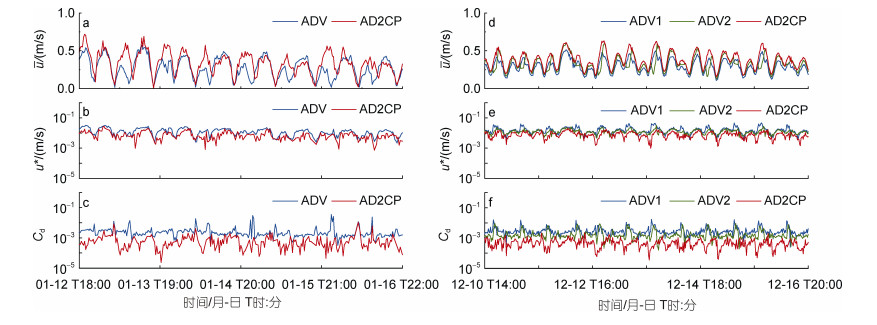 |
| 图 5 T1 (a~c)和T2 (d~f)站位的平均流速ū、摩阻流速u*和拖曳系数Cd Fig. 5 The time series of velocity along the major-axis ū, friction velocity u*, and drag coefficient Cd at T1 (a~c)station and T2 (d~f) station, respectively |
T1站位由ADV与AD2CP计算的近底部雷诺应力范围分别为1.3×10−6~1.0×10−3 m2/s2和7.5×10−7~ 1.0×10−3 m2/s2 (图 6a)。总体而言, 雷诺应力的大小主要受水平流速的控制, 两种仪器观测得到的雷诺应力差异并不大。雷诺应力剖面时间序列呈现出一定的周期变化, 在1.5×10−7~3.8×10−3 m2/s2范围内变动, 大多数时刻处于10−5~10−3量级之间(图 6b), 其高值主要出现于海底与海表附近, 低值则主要出现于中部水体。这可能是由于受到海底摩擦效应的影响, 底部湍流能够充分发育, 增强了水平动量的垂向通量; 而退潮时河流上层的羽流与水体剪切作用强烈, 加之海表附近可能受波浪能量输入的影响, 雷诺应力相应增大, 故而出现了底、表两个雷诺应力的高值区。
T2站位雷诺应力范围为3.2×10−7~2.0 ×10−3 m2/s2, 主要集中在10−5~10−3量级间, 高值区域主要分布在水体底层, 部分时刻上层也出现高值, 而低值区域主要集中于中层水体(图 6f)。同时, 在强波浪时刻, 整层水体雷诺应力均有增大, 且相对于强波浪存在约4 h的相位滞后。
T1、T2站位的湍动能剪切生成P集中在10−8~ 10−3 m2/s3 (图 6c和图 6h), 高值区主要分布在底、表层水体。湍流剪切生成受雷诺应力与水平流速的垂向梯度共同影响, 湍流剪切生成与雷诺应力的相位不尽相同。T1站位湍动能耗散率ε集中在10−7~ 10−3 m2/s3, 同样是底、表层水体较高(图 6d); T2站位湍动能耗散率现象与T1相似(图 6i)。T1站位浮力通量B为10−10~10−5 m2/s3 (图 6e), 其高值集中于底层水体, 低值集中于中层水体; T2站位浮力通量B为10−11~10−6 m2/s3 (图 6j), 分布相对较均匀, 在强波浪时刻整个水体出现浮力通量较高的现象。整体而言, 两站位由悬沙浓度变化引起的浮力通量较同层位的湍动能剪切生成、湍动能耗散率小1~2个数量级, 可忽略不计。
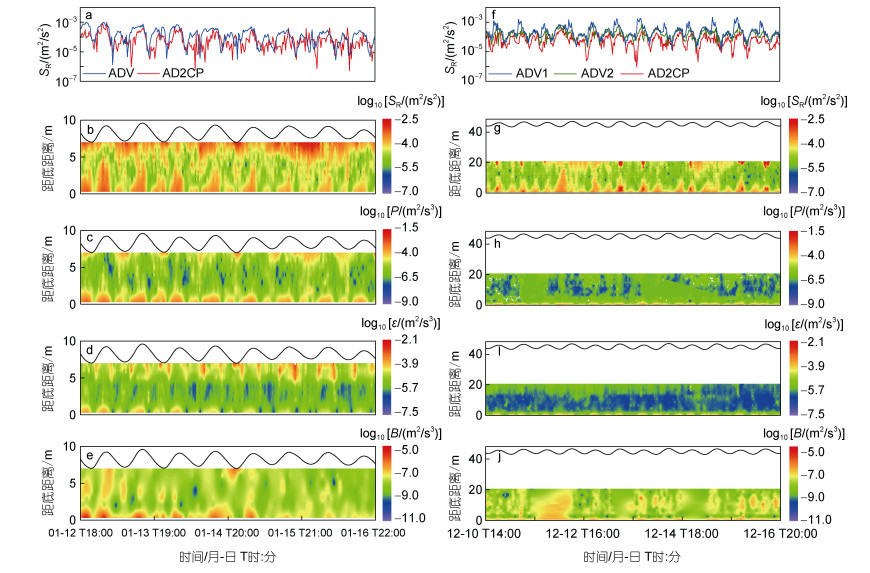 |
| 图 6 T1 (a~e)和T2 (f~j)站位近底部雷诺应力SR时间序列和所观测水体剖面的雷诺应力SR、湍动能剪切生成P、湍动能耗散率ε、浮力通量B剖面图 Fig. 6 The time series of Reynolds stress SR near the bottom and vertical profiles of Reynolds stress SR, turbulent kinetic energy production P, turbulent kinetic energy dissipation ε, and buoyancy flux B at T1 (a~e) station and T2 (f~j) station, respectively 注: b~e与g~j彩色等值线上方的黑色波浪线代表水位曲线 |
为了探究剪切和层化对湍流结构变化的影响, 本文将多个潮周期相位平均为一个完整的潮周期(Voulgaris et al, 2004)1672。因T1站位观测数据覆盖了整个水层, 故对其进行重点分析(图 7a~7e)。T1站位底层水体为强剪切、弱分层, 湍流混合作用强烈。在相对时间−12.5~ −9.5 h与0~3 h的落憩至初涨时间段内, 整个水层具有较高的剪切不稳定性, Ri虽大于经典临界值0.25, 但小于1, 水体混合相对较为均匀。存在强剪切的分层水体可发生剪切不稳定。在这一过程中, 湍流持续混合, 平均流的动能转化为湍动能耗散与浮力通量。在相对时间−3~ −1 h、8.5~11.5 h的涨憩至落急时间段内, 流速垂向剪切较弱, 而水体层化较强, Ri在整个水体内均处于高值, 这抑制了湍流的发育, 限制了湍动能的产生以及湍流混合, 因而出现了低湍动能剪切生成和低湍动能耗散率的现象。熊龙兵等(2014)也观测到类似的现象。T2站位近底层水体混合均匀, 湍流充分发育; 中上层水体Ri量级大多处于100~102范围内, 水体较弱的剪切以及较强的层化状态一定程度上抑制了湍流的发育(图 7f~7j)。
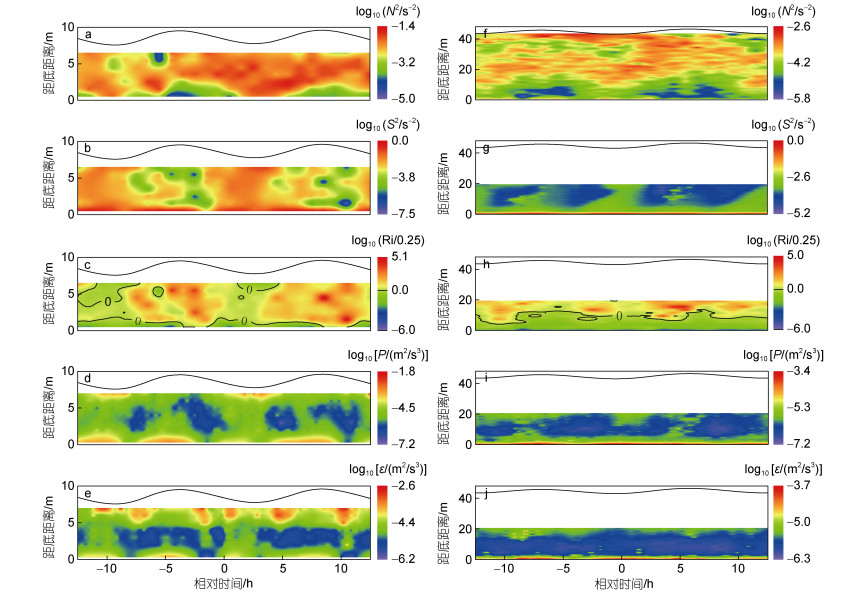 |
| 图 7 相位平均后T1 (a~e)和T2 (f~j)站位的浮力频率N2、流速剪切S2、理查森数Ri、湍动能剪切生成P以及湍动能耗散率ε剖面图 Fig. 7 The phase-averaged vertical profiles of buoyancy frequency N2, square vertical shear S2, Richardson number Ri, turbulent kinetic energy production P, and turbulent kinetic energy dissipation ε at T1 (a~e) and T2 (f~j) stations, respectively 注: 图中彩色等值线上方的黑色波浪线代表水位曲线 |
在河口地区, 外部能量输入、水体与海底边界摩擦、水体对流、水体与海岸相互作用等均可产生湍流, 导致湍动能ETK 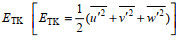
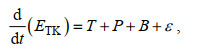 (22)
(22)其中, 左式代表ETK时间变化率; T为能量通量的散度, 包括脉动压力做功项、对流项以及黏性输运项。假设湍动能方程中的T、B可忽略不计, 则存在着P与ε间的局地平衡。
将多个潮周期的湍流垂向结构数据在涨、落潮阶段分别进行平均化处理, 用以进行局地平衡特征分析, 并计算参数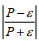
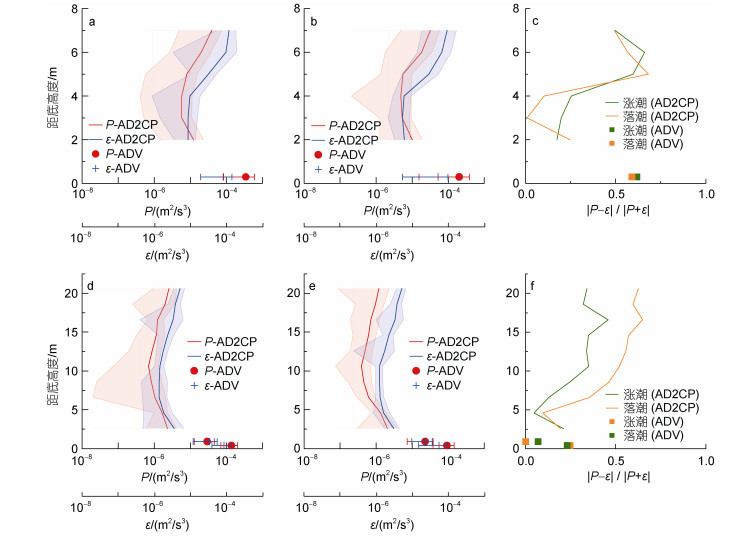 |
图 8 T1和T2站位湍流垂向结构 Fig. 8 Vertical structure of turbulence at T1 and T2 stations 注: a和b分别为T1站位涨潮阶段、落潮阶段湍动能剪切生成P和湍动能耗散率ε; c为T1站位涨潮阶段、落潮阶段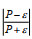 ; d和e分别为T2站位涨潮阶段、落潮阶段湍动能剪切生成P和湍动能耗散率ε; f为T2站位涨潮阶段、落潮阶段 ; d和e分别为T2站位涨潮阶段、落潮阶段湍动能剪切生成P和湍动能耗散率ε; f为T2站位涨潮阶段、落潮阶段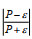 ; 图中阴影部分表示数据的标准差 ; 图中阴影部分表示数据的标准差 |
在近岸水体中, 湍动能的源主要有两部分, 一部分来自于海底底部摩擦, 另一部分则是海表波浪的能量输入(Grasso et al, 2012; Talke et al, 2013)。T1站位底摩擦产生的湍动能向上运输, 导致近底部的湍动能剪切生成大于湍动能耗散率与浮力通量之和。由于湍动能在水体中的垂向扩散, 湍动能剪切生成与湍动能耗散率均随着距底高度的增加而减小, 涨潮时距底3 m处、落潮时距底2 m处达到局地平衡, 上层水体则表现出湍动能耗散率大于湍动能剪切生成的现象。另外, 由于落潮时河流羽流与水体的剪切作用增强, 并且海表处常常伴随波浪的能量输入, 中上层水体的湍动能剪切生成与湍动能耗散率又逐渐增大。在本文中, 浮力通量是基于温盐恒定、密度变化仅由悬沙浓度变化引起的假定条件计算得到, 比湍动能剪切生成与湍动能耗散率小1~2数量级, 可忽略不计。但刘兴泉等(2004)、王鹏皓(2020)表明, 长江口区域内温盐结构可能发生活跃变化, 因此, 在水体层化结构稳定的T1站位, 无法排除浮力通量对湍动能非局地平衡的影响。综上所述, T1站位的湍动能非局地平衡可能为温盐等斜压作用引起的浮力通量与对流共同作用所致。
T2站位的湍流垂向结构与T1站位相似, 湍动能剪切生成与湍动能耗散率, 二者差异在上层水体处最大(图 8f), 落潮阶段的湍动能剪切生成与湍动能耗散率比涨潮阶段分别小了39.1%与24.7% (图 8d和图 8e)。T2站位水体基本处于混合均匀或弱层化状态(浮力通量可忽略不计), 观测期间有强波浪事件(有效波高大于2 m), 在强波浪作用下, 波浪破碎通过影响脉动压力做功与黏性输运, 对湍流场造成显著影响(Scully et al, 2016)。因此T2站位可能是由对流、脉动压力做功与黏性输运共同作用引起的。
4 结论本文在长江口及其邻近海域不同水深的区域(8.2 m, 44.7 m)采用新型5波束Signature 1 000 kHz AD2CP和ADV为主要仪器进行座底式观测, 得出以下主要结论:
(1) 基于ADV和AD2CP获得的近底部边界层参数(摩阻流速、拖曳系数以及雷诺应力)结果基本一致, 两种仪器的组合观测能在一定程度上提高湍流剖面观测的时空解析度。
(2) 长江口南槽受径流作用影响显著, 在水体混合较为均匀的落憩至初涨时刻, Ri的量级范围约为10−6~100, 强剪切作用促进了湍流混合; 在水体层化结构稳定性较强的涨憩至落急时刻, Ri约为100~104, 湍流混合被抑制。水下三角洲前缘海域由于距入海口较远, 其水体混合程度强于近岸海域, Ri多处于10−6~102。
(3) 研究区湍动能主要有底层摩擦与海面波浪两种能量输入源。底摩擦作用致使底层出现P > ε的湍流非局地平衡现象, 过剩的湍动能通过拟序结构向上迁移, 致使底层上方水体的湍流特征参数逐渐减弱且P的衰减程度强于ε。由于波浪能量的输入以及落潮时河口上层羽流所产生的强剪切, 海表处P、ε增大且出现P < ε的现象, 水体呈现向下消耗的湍流耗散结构。受近岸径流作用的影响, 长江口南槽湍流非局地平衡现象的主因可能为湍动能方程中温盐变化引起的浮力通量以及对流效应。而长江水下三角洲前缘海域湍流非局地平衡现象可能是对流和强波浪作用影响的脉动压力做功、黏性输运因素导致的。
由于现场观测的时空局限性, 在未来研究中, 将进一步开展空间尺度上湍流能量通量的散度研究、完善不同季节长江口海域的观测, 这对于充分了解湍流混合、认知河口物质输运、构建高精度模型具有重要意义。
致谢 南京大学唐杰平、陈德志、卢婷、兰庭飞与华东师范大学盛辉、汤碧璇、常洋参加了现场观测及样品处理分析工作, 同济大学涂俊彪、孟令鹏在数据处理方面给予诸多帮助, 谨致谢忱。
王鹏皓, 2020. 长江口海域环境要素分布及湍流混合[D]. 舟山: 浙江海洋大学: 21.
|
兰庭飞, 吴昊, 唐杰平, 等, 2019. 基于新型高频声学多普勒流速剖面仪的河口近底部边界层观测初探[J]. 海洋通报, 38(6): 640-649. |
刘兴泉, 侯一筠, 尹宝树, 2004. 东海沿岸海区垂直环流及其温盐结构动力过程研究Ⅱ. 温盐结构[J]. 海洋与湖沼, 35(6): 497-506. |
刘志宇, 2009. 强潮驱陆架海中的湍流与混合[D]. 青岛: 中国海洋大学: 5, 11.
|
时钟, 2001. 长江口水动力过程的研究进展(1979~1999)[J]. 海洋科学, 25(6): 54-57. |
汪亚平, 高抒, 李坤业, 1999. 用ADCP进行走航式悬沙浓度测量的初步研究[J]. 海洋与湖沼, 30(6): 758-763. |
汪亚平, 高建华, 潘少明, 2006. 长江河口区边界层参数的观测与分析[J]. 海洋地质动态, 22(7): 16-20. |
沈焕庭, 朱建荣, 1999. 论我国海岸带陆海相互作用研究[J]. 海洋通报, 18(6): 11-17. |
林姚坤, 包芸, 陈起程, 等, 2018. 夏季长江河口层化与湍流混合特征分析[J]. 热带海洋学报, 37(5): 33-39. |
鲁远征, 吴加学, 刘欢, 2012. 河口底边界层湍流观测后处理技术方法分析[J]. 海洋学报, 34(5): 39-49. |
熊龙兵, 2014. 长江河口环流与湍流混合: 数学模拟与理论计算[D]. 上海: 上海交通大学: 98-100.
|
熊龙兵, 浦祥, 时钟, 等, 2014. 潮汐应变对长江口北槽枯季湍流混合与层化的影响[J]. 海洋工程, 32(4): 41-57. |
BAKHODAY-PASKYABI M, FER I, REUDER J, 2018. Current and turbulence measurements at the FINO1 offshore wind energy site: analysis using 5-beam ADCPs[J]. Ocean Dynamics, 68(1): 109-130. DOI:10.1007/s10236-017-1109-5 |
BRICKER J D, MONISMITH S G, 2007. Spectral wave– turbulence decomposition[J]. Journal of Atmospheric and Oceanic Technology, 24(8): 1479-1487. DOI:10.1175/JTECH2066.1 |
DAVIES A M, GERRITSEN H, 1994. An intercomparison of three-dimensional tidal hydrodynamic models of the Irish Sea[J]. Tellus A, 46(2): 200-221. DOI:10.3402/tellusa.v46i2.15474 |
DEWEY R, STRINGER A S, 2007. Reynolds stresses and turbulent kinetic energy estimates from various ADCP beam configurations: theory[J]. Journal of Rhyscial Oceanography, 1: 35. |
FEDDERSEN F, WILLIAMS III A J, 2007. Direct estimation of the Reynolds stress vertical structure in the nearshore[J]. Journal of Atmospheric and Oceanic Technology, 24(1): 102-116. DOI:10.1175/JTECH1953.1 |
GRASSO F, CASTELLE B, RUESSINK B G, 2012. Turbulence dissipation under breaking waves and bores in a natural surf zone[J]. Continental Shelf Research, 43: 133-141. DOI:10.1016/j.csr.2012.05.014 |
GREEN M O, 1992. Spectral estimates of bed shear stress at subcritical Reynolds numbers in a tidal boundary layer[J]. Journal of Physical Oceanography, 22(8): 903-917. DOI:10.1175/1520-0485(1992)022<0903:SEOBSS>2.0.CO;2 |
GREEN M O, MCCAVE I N, 1995. Seabed drag coefficient under tidal currents in the eastern Irish Sea[J]. Journal of Geophysical Research: Oceans, 100(C8): 16057-16069. DOI:10.1029/95JC01381 |
GUERRA M, THOMSON J, 2017. Turbulence measurements from five-beam acoustic Doppler current profilers[J]. Journal of Atmospheric and Oceanic Technology, 34(6): 1267-1284. |
GUO X Y, YANAGI T, 1998. Three-dimensional structure of tidal current in the East China Sea and the Yellow Sea[J]. Journal of Oceanography, 54(6): 651-668. |
LI R Z, VOULGARIS G, WANG Y P, 2022. Turbulence structure and burst events observed in a tidally induced bottom boundary layer[J]. Journal of Geophysical Research: Oceans, 127(6): e2021JC018036. |
LOHRMANN A, 2001. Monitoring sediment concentration with acoustic backscattering instruments[S]. Nortek Technical Note3: 1-5.
|
MCDOUGALL T J, BARKER P M, 2011. Getting started with TEOS-10 and the Gibbs Seawater (GSW) Oceanographic Toolbox 2010[Z]. SCOR/IAPSO WG127(532), 1-28. http:∥www.TEOS10.org, 2011.
|
MESTAYER P G, CHAMPAGNE F H, FRIEHE C A, et al, 1978. Estimation of the fluxes over the ocean by the covariance and dissipation methods [M] // FAVRE A, HASSELMANN K. Turbulent Fluxes Through the Sea Surface, Wave Dynamics, and Prediction. New York, USA: Springer: 51-65.
|
RIPPETH T P, FISHER N R, SIMPSON J H, 2001. The cycle of turbulent dissipation in the presence of tidal straining[J]. Journal of Physical Oceanography, 31(8): 2458-2471. |
STACEY T M, MONISMITH G S, BURAU R J, 1999. Measurements of Reynolds stress profiles in unstratified tidal flow[J]. Journal of Geophysical Research: Oceans, 104(C5). |
SCULLY M E, TROWBRIDGE J H, FISHER A W, 2016. Observations of the transfer of energy and momentum to the oceanic surface boundary layer beneath breaking waves[J]. Journal of Physical Oceanography, 46(6): 1823-1837. |
SHERWOOD C R, LACY J R, VOULGARIS G, 2006. Shear velocity estimates on the inner shelf off Grays Harbor, Washington, USA[J]. Continental Shelf Research, 26(17/18): 1995-2018. |
SIMPSON J H, BROWN J, MATTHEWS J, et al, 1990. Tidal straining, density currents, and stirring in the control of estuarine stratification[J]. Estuaries, 13(2): 125-132. |
SOULSBY R L, DYER K R, 1981. The form of the near-bed velocity profile in a tidally accelerating flow[J]. Journal of Geophysical Research: Oceans, 86(C9): 8067-8074. |
TALKE S A, HORNER-DEVINE A R, CHICKADEL C C, et al, 2013. Turbulent kinetic energy and coherent structures in a tidal river[J]. Journal of Geophysical Research: Oceans, 118(12): 6965-6981. |
THORNE P D, VINCENT C E, HARDCASTLE P J, et al, 1991. Measuring suspended sediment concentrations using acoustic backscatter devices[J]. Marine Geology, 98(1): 7-16. |
THORPE S A, 2007. An Introduction to Ocean Turbulence [M]. Cambridge, UK: Cambridge University Press, 1-2.
|
TROWBRIDGE J H, GEYER W R, BOWEN M M, et al, 1999. Near-bottom turbulence measurements in a partially mixed estuary: turbulent energy balance, velocity structure, and along-channel momentum balance[J]. Journal of Physical Oceanography, 29(12): 3056-3072. |
TURNER J S, BENTON E R, 1974. Buoyancy effects in fluids[J]. Physics Today, 27(3): 52-53. |
URICK R J, 1983. Principles of Underwater Sound[M]. 3rd edn. New York, USA: McGraw-Hill Book Company, 1-95.
|
VOULGARIS G, MEYERS S T, 2004. Temporal variability of hydrodynamics, sediment concentration and sediment settling velocity in a tidal creek[J]. Continental Shelf Research, 24(15): 1659-1683. |
VOULGARIS G, TROWBRIDGE J H, 1998. Evaluation of the acoustic doppler velocimeter (ADV) for turbulence measurements[J]. Journal of Atmospheric and Oceanic Technology, 15(1): 272-289. |
WANG X H, 2002. Tide-induced sediment resuspension and the bottom boundary layer in an idealized estuary with a muddy bed[J]. Journal of Physical Oceanography, 32(11): 3113-3131. |
WANG J F, MACDONALD D G, ORTON P M, et al, 2015. The effect of discharge, tides, and wind on lift-off turbulence[J]. Estuaries and Coasts, 38(6): 2117-2131. |
ZHANG Q J, WU J X, 2018. On the phase lag of turbulent dissipation in rotating tidal flows[J]. Continental Shelf Research, 156: 23-32. |
 2023, Vol. 54
2023, Vol. 54


