
中国海洋湖沼学会主办。
文章信息
- 胡明浩, 谢玲玲, 李明明, 梁朋. 2024.
- HU Ming-Hao, XIE Ling-Ling, LI Ming-Ming, LIANG Peng. 2024.
- 瑞利参数在海浪波高机器学习预测中的应用
- THE APPLICATION OF THE RAYLEIGH PARAMETER IN MACHINE LEARNING PREDICTION OF WAVE HEIGHT
- 海洋与湖沼, 55(2): 318-331
- Oceanologia et Limnologia Sinica, 55(2): 318-331.
- http://dx.doi.org/10.11693/hyhz20230900180
文章历史
-
收稿日期:2023-09-01
收修改稿日期:2023-11-18
2. 陆架及深远海气候、资源与环境广东省高等学校重点实验室 广东湛江 524088;
3. 自然资源部空间海洋遥感与应用重点实验室 广东湛江 524088
2. Key Laboratory of Shelf and Deep-sea Environment and Resources of Guangdong Higher Education Institutes, Zhanjiang 524088, China;
3. Key Laboratory of Spatial Ocean Remote Sensing and Application, Ministry of Natural Resources, Zhanjiang 524088, China
海浪是海洋中一种常见的、复杂的波动现象, 受风速、风向、地形等因素的影响。海浪波高的时空变化很大, 其通常为几厘米到几米, 但在深远海以及极端天气条件下可达几十米。海浪的随机性对海上航行安全、海上作业以及海洋能的开发利用等带来了挑战。波高是描述波浪特征的核心参数之一, 准确地预测波高对保障海上安全、提高波浪能利用率和能源结构稳定性具有重要意义(Deo et al, 2001; Jain et al, 2006, 2011; Dixit et al, 2016)。
波高的预测一直都是海浪研究的热点问题(陈希等, 2002)。传统的预测主要为经验预测(Wilson, 1965; Ge et al, 2016)和数值模型预报(Hasselmann et al, 1973; Lionello et al, 1998; The Swamp Group, 2013)。经验预测是通过对历史观测数据按照时间先后进行外推, 进而得到相关海浪状态的预期数值。这种方法主要依靠历史数据和传统分析相结合, 在实用性和准确度方面都存在较大局限性(孟雷等, 2010)。随着数学和计算机科学的发展, 数值模拟成为海浪预报的主要手段, 先后发展了SWAN (梁小力等, 2015)和WAVEWATCH-Ⅲ (Wang et al, 2017)等多个海浪预报模式。然而, 数值模拟需要高性能计算机和显著的时间成本(Etemad-Shahidi et al, 2009; Wang et al, 2018), 难以满足紧急情况下的快速预报。近几年, 随着人工智能技术发展, 各种神经网络或混合模型逐步用来预测海浪高度(Deo et al, 2001; James et al, 2018)。Deo等(1998)提出了一种前馈网络来实时预测海浪高度, 发现与自回归模型相比, 该方法具有更强的通用性、灵活性和适应性。Makarynskyy (2004)以波高数据为输入搭建了神经网络。Tsai等(2002)将反向传播(back-propagation, BP)神经网络技术应用于短期海浪预测和数据补充, 并对比了不同的训练测试对预测结果的影响。Fan等(2020)利用LSTM (longshort-term memory)模型预测有效波高, 验证了LSTM模型具有较强的长期预测能力, 同时提出了数值模式与深度学习结合的SWAN-LSTM模型进行单点预测, 其精度比标准SWAN模型提高了65%以上。李自立等(2022)提出了残差记忆网络(LSTM-ResNet)模型对定点进行有效波高预测, 结果表明该模型对短时波高的预测优于反向传播神经网络(back-propagation neural network, BPNN)模型和LSTM模型。李海涛等(2022)构建了基于随机森林(random forest, RF)的注意力机制与双向长短期记忆神经网络(bidirectional- long short-term memory, BiLSTM)相结合的海浪预测模型(random forest-bidirectional-long short-term memory, RF-BiLSTM), 结果显示, 和BP、LSTM、BiLSTM模型相比, RF-BiLSTM模型的预测精度更高, 拟合程度更好。Mahjoobi等(2009)尝试使用支持向量机(support vector machine, SVM)来预测波高, 结果表明, 支持向量机模型具有可接受的精度, 并且计算时间少于人工神经网络模型。Elbisy (2015)则提出SVM结合遗传算法(genetic algorithm, GA)的组合模型来预测有效波高。Duan等(2016)提出了一种经验模型分解(empirical model decomposition, EMD)和支持向量回归(support vector machine regression, SVR)的混合模型, 即EMD-SVR模型, 用于非线性和非平稳波动的预测, 打破了传统的统计模型在预测非线性和非平稳波时存在局限性。张振全等(2021)提出了一种基于平均交互信息(adjusted mutual information, AMI)特征选择的自回归模型(auto-regressive, AR)与SVR混合的短期有效波高预测算法, 预测结果表明, AR-SVR混合模型预测结果优于单一的AR和SVR模型。
上述研究将机器学习算法引入波浪预测, 推动了波高的预测。然而, 仅通过数据驱动的机器预测难以解释其中的物理原理, 同时也制约了预测效果提升。在机器学习模型中引入物理约束(Zhu et al, 2022; Ouyang et al, 2023), 是解决这一挑战的一种有前途的方法。因此, 本研究尝试将反映波高统计特征的瑞利参数作为物理约束引入到传统机器学习模型, 并基于山东小麦岛站点的长时间波浪数据进行建模研究, 通过引入瑞利参数前后的预测结果对比, 分析瑞利参数对于基于机器学习的波高预测模型的有效性。
1 数据与方法 1.1 数据来源与处理本研究所用数据来自国家海洋科学数据中心, 为2015年7月~2022年6月山东小麦岛观测站的实测数据(http://mds.nmdis.org.cn/), 站位如图 1星号所示。数据集包含波高、风速、风向以及气压、海表温度等参数, 采样间隔为1 h。数据的样本点总数为61 368个。因为天气或者设备原因, 约11.7% (共7 262个样本点) 的数据丢失。为了便捷地分析批量数据和准确地预测波高, 本研究对零散丢失数据用线性插值进行处理。但因2018年1月、4月和6月以及2020年9~10月整个月份的数据出现丢失的情况, 因此本研究这些时段数据缺失。
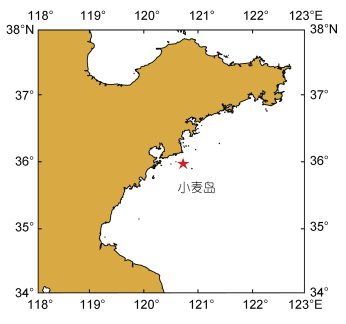 |
| 图 1 山东小麦岛海浪观测站的地理位置 Fig. 1 Geographical location of the Xiaomai Island Wave Observation Station in Shandong |
图 2给出了插值和质量控制后的观测风速、风向、气压和波高的时间序列。观测期间风速大多在2~4 m/s, 平均风速为3.56 m/s, 最大风速为17.4 m/s。冬季以北风为主, 夏季以东风为主。气压多在1 000~ 1 030 Pa, 观测期间平均大气压强为1 015.7 hpa, 最高气压1 042 hpa, 最低气压980.4 hpa, 总体呈冬强夏弱的趋势。波高的统计特征如图 3的柱状图所示, 总体呈现瑞利分布特征, 其瑞利参数为0.42, 最大概率波高为0.3 m, 均值为0.56 m, 标准差为0.33 m, 最大值和最小值分别为3.3 m和0.1 m。
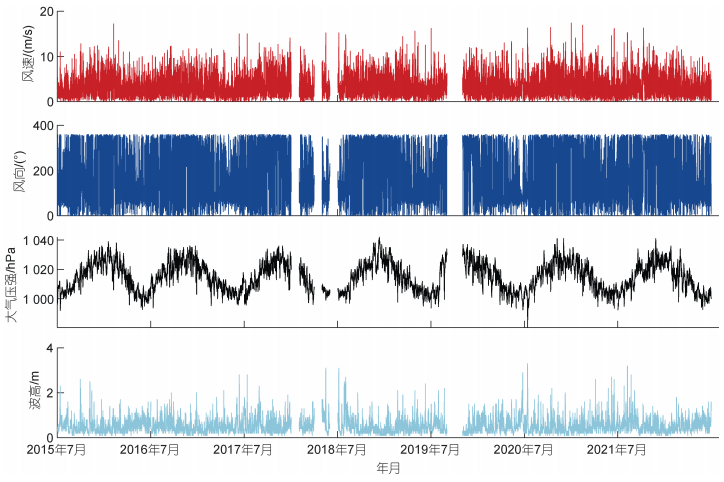 |
| 图 2 2015年7月~2022年6月山东小麦岛站点实测风速、风向和大气压强和波高时间序列图 Fig. 2 The time series of the measured values of wind speed, wind direction, atmospheric pressure, and wave height at the Xiaomai Island station in Shandong from July 2015 to June 2022 |
瑞利分布是最常见的用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性的一种分布类型(Lin, 2000)。其概率密度函数(probability density function, PDF)表示为
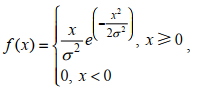 (1)
(1)其中, x是随机变量的取值, σ代表了尺度参数也称为瑞利参数, 决定着分布的形状。则瑞利参数与期望E(X)和方差D(X)满足以下关系式:
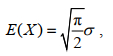 (2)
(2)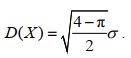 (3)
(3)图 3给出了观测期间山东小麦岛站点波高统计分布。由波高概率分布, 可见其大致呈现瑞利分布。本研究假设原数据中的波高统计服从瑞利分布, 并用模糊估计方法(陈水利等, 2005; 张鑫等, 2008)来验证每月的波高分布是否服从瑞利分布。以2015年7月为例, 验证具体步骤如下。
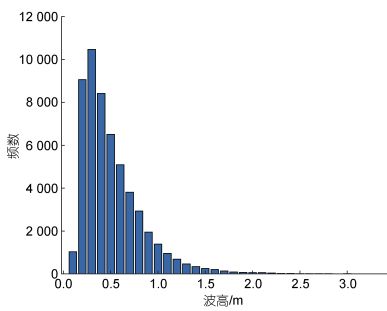 |
| 图 3 2015年7月~2022年6月山东小麦岛站点实测波高统计分布图 Fig. 3 The distribution of measured wave height at the Xiaomai Island station in Shandong from July 2015 to June 2022 |
第一步: 由观测样本可以得到2015年7月的均值和方差分别为0.58 m和0.31 m2, 从而由式(2)求出瑞利参数σ1≈0.46, 由式(3)求出σ2≈0.47, 二者近似。
第二步: 采用模糊估计方法量化2015年7月波高服从瑞利分布的概率。由第(1)步求得的σ1和σ2计算隶属函数μA (陈水利等, 2005):
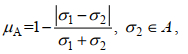 (4)
(4)结果为0.989, 即此组数据有98.9%的可能服从瑞利分布。
以同样的方法计算出其他月份波高统计服从瑞利分布的概率均为90%以上, 平均为94.9%, 说明所用的波高数据的确服从瑞利分布。
1.2.2 瑞利参数的计算对每个月的波高数据进行瑞利分布拟合, 可以得到2015年7月~2020年8月每月波高的瑞利参数(如图 4黑色点所示)和2020年11月~2022年6月每月波高的瑞利参数(如图 4中蓝色点所示), 其中数据丢失的2018年1月、4月和6月的瑞利参数则分别取前一个月和后一个月瑞利参数的平均值。为了得到测试集中每个月的瑞利参数, 对2015年7月~2020年8月的瑞利参数进行多项式回归, 可得到瑞利参数(σ)和月份序数(x)的函数关系(如图 4红线所示), 拟合优度0.81, 拟合效果较好。由该函数关系, 计算可得2020年9月~ 10月两个空缺月份的瑞利参数, 其在2020年11月~ 2022年6月的拟合值(红线)与实测值(蓝点)也比较接近。
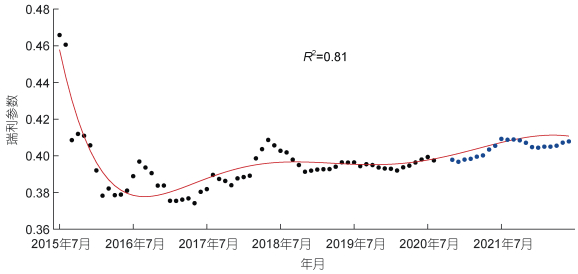 |
| 图 4 2015年7月~2020年8月小麦岛波高统计分布的瑞利参数(黑色点)以及其拟合曲线(红色线) Fig. 4 The Rayleigh parameters (black dots) and their fitting curve (red line) of the wave height distribution at the Xiaomai Island from July 2015 to August 2020, and the Rayleigh parameters observed from November 2020 to June 2022 (blue dots) 注: R2表示拟合优度; 蓝色点为2020年11月~2022年6月观测得到的瑞利参数 |
本研究应用BPNN、LSTM和支持向量机回归(support vector regression, SVR)三种机器学习算法。其中BPNN模型使用了Back-propagation算法, 是最传统的神经网络, 它具有较强的非线性映射能力, 同时有不错的泛化能力, 即将学习成果应用于新知识的能力(Chakraborty et al, 1992)。LSTM模型是解决时序预测的常用方法(Asuero et al, 2006; Qi et al, 2019), 它解决了循环神经网络(recurrent neural network, RNN)模型中存在的长期依赖问题。而SVM模型是一种监督式学习的方法, 可广泛地应用于统计分类以及回归分析, 该方法用于数据回归时又称为SVR, 具有简单高效的特点(周志华, 2016)。这些方法也是人工智能预测海浪最常用的模型。
本文设定模型输入为当前时刻的波高数据及其可能的影响因素(气压、风速和风向), 模型输出为未来1、6、12、24 h的预测波高数据。为了保证时间的连续性, 实验时, 选取2015年7月~2017年12月的连续数据为训练集, 用于模型建模训练, 2018年7月~2020年8月的数据作为验证集, 而2020年11月~ 2022年6月的数据作为模型的测试集, 用于模型预测效果测试分析。
为了检验机器学习模型在引入瑞利参数之后预测效果的提高, 本研究设计了3组对照实验, 分别对比了BPNN、LSTM以及SVR模型在加入瑞利参数作为输入变量前后的预测效果, 实验流程如图 5所示。
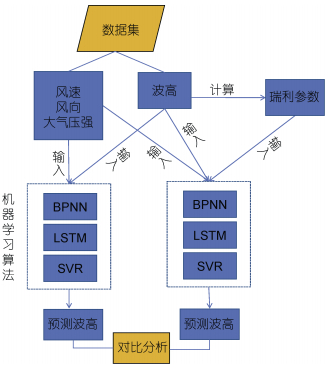 |
| 图 5 实验流程图 Fig. 5 Flowchart of the experiment 注: BPNN表示反向传播神经网络(back-propagation neural network); LSTM表示长短记忆网络(long short-term memory); SVR表示支持向量机回归(support vector regression) |
特征重要性是指在机器学习模型中, 用于衡量各个特征对模型预测结果的贡献程度的指标。了解机器学习中的特征重要性可以增强模型的可解释性, 利于参数降维和参数选择(Zhou et al, 2019), 提升模型效率(Blum et al, 1997)。机器学习中特征重要性的计算主要有SHAP (Shapley Additive exPlanation)法(Lundberg et al, 2017, 2018, 2020)、特征扰动方法、蒸馏学习法(Hinton et al, 2015)、基于机器学习可解释的方法和基于线性回归模型的权重的方法, 其中特征扰动方法相对简单, 应用广泛(刘子怡等, 2022)。本研究中采取了特征扰动方法计算输入参数的重要性。算法的核心思路是先训练一个机器学习模型, 在计算第i个特征重要性时, 打乱第i个特征, 然后计算打乱后的预测结果的指标变化, 通过比较这个指标变化大小来判断特征的重要程度。
2 实验结果与分析本文基于山东小麦岛的波高实测数据, 以2015年7月~2017年12月每小时的观测数据为训练集, 2018年7月~2020年8月的数据为验证集, 2020年11月~2022年6月的数据为测试集, 分别利用BPNN、LSTM和SVR模型对该地区波高进行预测, 并对比有无瑞利参数作为输入特征的预测结果。实验结果如图 6~8所示。
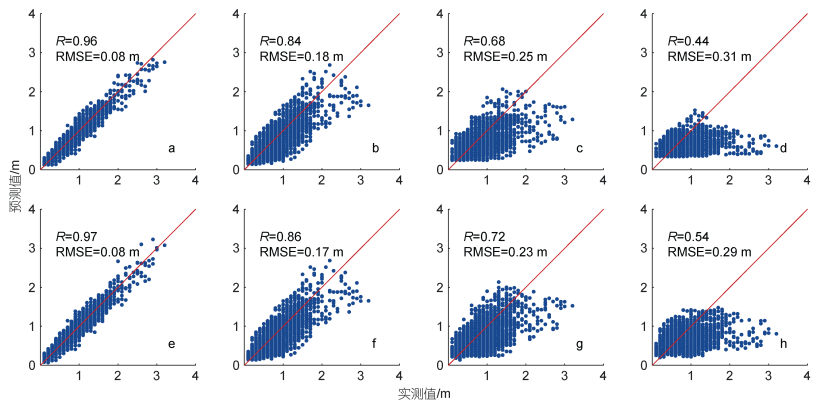 |
| 图 6 BPNN模型在1 h (a, e)、6 h (b, f)、12 h (c, g)和24 h (d, h)的预测时间范围内预测的波高与观测值之间的比较 Fig. 6 Comparisons between observed and predicted wave heights by BPNN in 1 h (a, e), 6 h (b, f), 12 h (c, g), and 24 h (d, h) 注: a~d: 未引入瑞利参数的结果; e~h: 引入瑞利参数后的结果; R表示相关系数; RMSE表示均方根误差 |
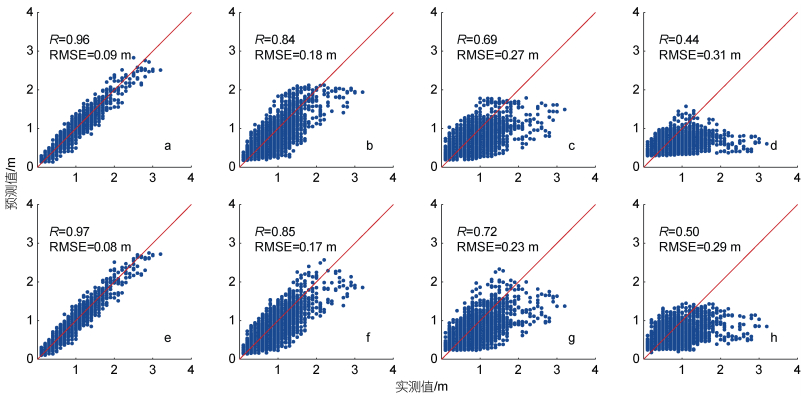 |
| 图 7 LSTM模型在1 h (a, e)、6 h (b, f)、12 h (c, g)和24 h (d, h)的预测时间范围内预测的波高与观测值之间的比较 Fig. 7 Comparisons between observed and predicted wave heights by LSTM in 1 h (a, e), 6 h (b, f), 12 h (c, g), and 24 h (d, h) 注: a~d未加入瑞利参数, e~h为引入瑞利参数后的结果 |
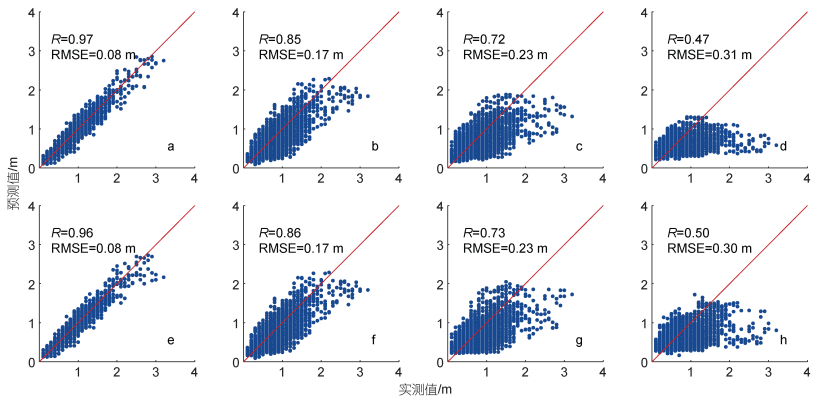 |
| 图 8 SVR模型在1 h (a, e)、6 h (b, f)、12 h (c, g)和24 h (d, h)的预测时间范围内预测的波高与观测值之间的比较 Fig. 8 Comparisons between observed and predicted wave heights by SVR in 1 h (a, e), 6 h (b, f), 12 h (c, g) and 24 h (d, h) 注: a~d未加入瑞利参数, e~h为引入瑞利参数后的结果 |
图 6为BPNN模型(a~d)及其引入瑞利参数(e~h)后在1、6、12和24 h时段预测的观测值与预测值的对比。可见, 随着预报时间增长, BPNN预报效果降低。在1 h的预测中, BPNN模型(图 6a)及其引入瑞利参数后(图 6e)的表现大致相同, 预测值与测试集观测波高的均方根误差(root mean square error, RMSE)分别为0.09和0.08 m, 相关系数(R)分别为0.96和0.97。由此可见, 在短期预测中, 引入瑞利参数对波高的预测结果稍有提升。BPNN模型在6 h的预测中, RMSE为0.18 m (图 6b), 而在引入瑞利参数后降至0.17 m (图 6f), 仅变化0.01 m, 但R由引入前的0.84升至0.86, 增加0.02; 在12 h的预测中(图 6c和6g), RMSE从0.25 m降至0.23 m, 降低0.02 m, R从0.68升至0.72, 增加0.04; 在24 h的预测中(图 6d和6h), 预测结果的RMSE由0.31 m降至0.29 m, R从0.44升至0.51, 增加0.07。由此可见, 在12~24 h的中长期预测中, 瑞利参数引入对预测结果相关性的提高有明显帮助。
图 7为LSTM模型(a~d)及其引入瑞利参数(e~h)后在1、6、12和24 h时预测值与观测值对比。可见, 在1和6 h的预测中, 引入瑞利数前后(a~b和e~f), RMSE降低0.01 m, R增加0.01; 在12 h的预测中(图 7c和7g), RMSE在引入瑞利参数后则显著降低0.04 m, 从0.27 m降至0.23 m, R也增加0.03, 从0.69升至0.72; 在24 h的预测中(图 7d和7h), RMSE从0.31 m降0.02 m至0.29 m, R从0.44升至0.50, 增加0.06。由此可见, 与BPNN模型结果类似, LSTM模型在12~24 h中长期的预测中, 引入瑞利参数后预测效果提高。
图 8为SVR模型(a~d)及其引入瑞利参数(e~f)后在1 h、6 h、12 h和24 h时预测值与观测值的对比。由图可见, 在1h、6h和12h的预测中(a~c和e~g), 引入瑞利参数对SVR模型预测波高的效果提高并不明显, 其中RMSE并没有发生变化, R甚至减小, 但是在24 h的预测中(图 8d和8h), 引入瑞利参数后, RMSE从0.31 m降至0.30 m, R从0.47升至0.50。瑞利系数引入对SVR模型长期预测也是有意义的。
综上, 从图 6~8可见, 随着预测时间的逐渐加长, 三种方法的预报有效性均不断降低, RMSE数值逐渐增大近4倍, R数值不断减小近一半, 其中SVR方法的性能衰减程度相对较慢, 在全时段的预测中SVR预报的R值稍优于BPNN和LSTM模型。在1 h的预测中, 三种机器学习方法及其引入瑞利数后的表现差异不大, 瑞利参数引入对预测结果提升不大。在6、12和24 h的预测中, BPNN和LSTM模型在引入瑞利参数后RMSE下降、r升高, 而SVR方法的预测结果与未引入参数时相比变化相对较小。相比BPNN, LSTM模型在12和24 h预测RMSE更大, 在引入瑞利参数后, 二者相当了, 说明瑞利参数引入利于解决了LSTM模型的梯度消失问题。
从图 6~8中的散点分布情况还可以看到, 在引入瑞利参数之前, 各模型在12和24 h的预测中, 预测结果总体偏小。为了清楚看到12和24 h的预测中预测结果的偏小是否得到改善, 我们计算了引入瑞利参数前后的预测值和观测值偏差的绝对值平均(mean absolute error, MAE), 结果如表 1所示。可以看到, 引入瑞利参数后, 三个模型的MAE均有所减小, 尤其是在BPNN和LSTM模型。图 9进一步展示了三种模型有无瑞利参数在12 h预测中预测偏差的时间序列, 左侧为冬季(2020年12月~2021年2月), 右侧为夏季(2021年6月~8月)。可见, 引入瑞利参数后, 各模型的预测偏差(红实线)几乎在整个时间序列中均小于引入前(蓝实线), 尤其是在夏季月份, 对BPNN模型, 冬季和夏季平均MAE分别为0.16和0.22 m, 引入瑞利参数后则分别下降为0.14和0.17 m, 各减少了12.5%和22.5%。对LSTM模型和SVR模型, 冬季预测MAE减少了11.8%和6.7%, 夏季MAE则减少了19.0%和13.6%。可见, 夏季月份引入瑞利参数后预测MAE减小显著, 这可能与瑞利参数拟合在2021年夏季月份更准确有关(图 4)。24 h预测结果类似(图未展示), BPNN、LSTM和SVR三种方法冬季MAE分别下降11.1%、15.8%和11.1%, 夏季下降了22.2%、19.2%和20.7%。瑞利参数的引入, 提高了基于机器学习模型的波高预测效果。
| 预测模型 | 预测时间/h | 引入瑞利参数前MAE/m | 引入瑞利参数后MAE/m | |||||
| 全部(2020年11月~2022年6月) | 冬季 (2020年12月~2021年2月) |
夏季 (2021年6月~8月) |
全部(2020年11月~2022年6月) | 冬季 (2020年12月~2021年2月) |
夏季 (2021年6月~8月) |
|||
| BPNN | 12 | 0.18 | 0.16 | 0.22 | 0.16 | 0.14 | 0.17 | |
| 24 | 0.22 | 0.18 | 0.27 | 0.20 | 0.16 | 0.21 | ||
| LSTM | 12 | 0.18 | 0.17 | 0.21 | 0.16 | 0.15 | 0.17 | |
| 24 | 0.23 | 0.19 | 0.26 | 0.20 | 0.16 | 0.21 | ||
| SVR | 12 | 0.16 | 0.15 | 0.22 | 0.16 | 0.14 | 0.19 | |
| 24 | 0.21 | 0.18 | 0.29 | 0.20 | 0.16 | 0.23 | ||
| 注: BPNN表示反向传播神经网络(back-propagation neural network); LSTM表示长短记忆网络(long short-term memory); SVR表示支持向量机回归(support vector regression) | ||||||||
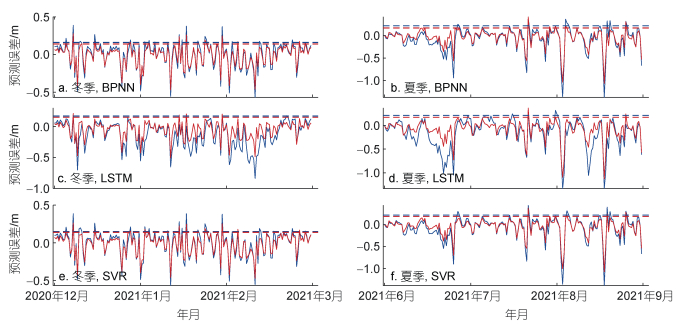 |
| 图 9 三种模型在12 h预测中预测波高与观测值之间的偏差时间序列 Fig. 9 Time series of the forecasting errors between observation and the 12 h prediction in three models 注: a、c和e为冬季(2020年12~2021年2月)的预测误差, b、d和f为夏季(2021年6~8月)的预测误差; 蓝红实线分别表示为引入瑞利参数前后的预测偏差, 蓝红虚线为偏差绝对值的平均(MAE) |
上文分析显示, 瑞利参数的引入增强了波高的预报效果。为进一步量化瑞利参数重要性, 本文采用了特征扰动方法进行评估。将BPNN、LSTM和SVR三个模型输入的大气压强(PA)、风向(DW)、风速(SW)和瑞利参数(NR)分别进行特征扰动, 然后分别计算特征扰动之后的预测结果评价指标与扰动前的相关系数和均方根误差的差异∆R和∆RMSE来判断各模型中输入特征的重要性。图 10给出了基于特征扰动方法对BPNN (图 10a~10b)、LSTM (图 10c~10d)和SVR模型(图 10e~10f)输入特征重要性评估的结果, 垂向的柱状条表示特征扰动前后的差异量, 其中∆R为减少量, ∆RMSE为增加量。从图 10可以看出, 对近岸风浪的波高, DW和SW在三个模型中均为最重要参数, 其扰动变化占比最高。瑞利参数(NR)占比随预测时长增大而增大, 在BPNN模型中最为明显。
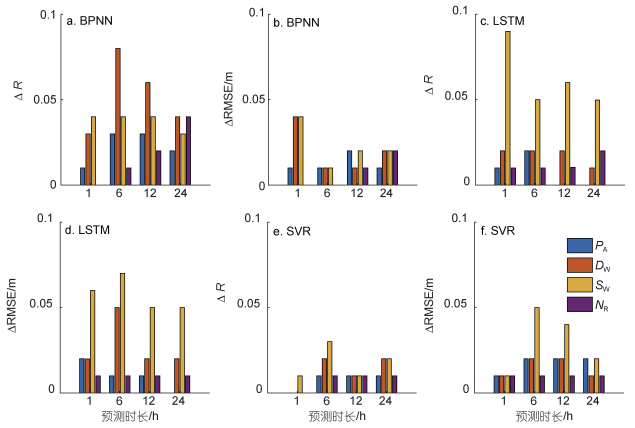 |
| 图 10 BPNN模型(a~b)、LSTM模型(c~d)和SVR模型(e~f)对各特征进行扰动后的预测结果的评价指标的变化量 Fig. 10 Changes in evaluation indicators of predicted results by the BPNN model (a~b), LSTM model (c~d), and SVR model (e~f) after perturbation of each feature 注: PA、DW、SW和NR分别表示大气压强、风向、风速和瑞利参数 |
BPNN模型(图 10a~10b)在各时长的预测中对瑞利参数进行特征扰动后, 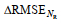
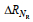
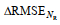
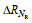
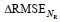
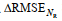
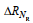
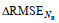
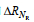
上述结果显示, 瑞利参数对BPNN和LSTM模型的提升主要体现在中长期预测, 短期预测不太明显, 而瑞利参数对于SVR模型的预测效果的提升并不大, 但预测效果指标的变化量在总变化量中的占比较大, 说明了引入瑞利参数对模型预测性能提升的重要性。
4 讨论 4.1 波高分布的拟合对于海浪的波高分布函数最早由Longuet-Higgins (1952)提出, 他在理论上证明线性海浪的波高服从瑞利分布。Forristall (1978)提出了波高的Weibull分布, 该分布解决了瑞利分布在大波高概率方面的问题。瑞利分布与Weibull分布在概率分布图上具有相似性。本研究中, 我们也对2015年7月至2022年6月的波高数据进行了Weibull分布的拟合和模糊理论验证, 验证结果显示原数据符合Weibull分布的概率为96.7%, 略高于瑞利分布94.9%的概率。鉴于二者分布相似、概率相当, 且瑞利参数与波高统计的均值与众数可以直接建立联系, 本研究假定波高分布符合瑞利分布。
本研究中的瑞利参数是由基于月份的拟合函数计算得到, 其量值随着预测时间增加缓慢增加趋势, 与实测计算结果类似(图 3)。关系式拟合可能使得到的瑞利参数不够准确。在实际情况中, 可以利用拟合的曲线得出未来一个月的瑞利参数, 并在下月预测前重新引入该月实测结果。由此, 可以提高瑞利参数的准确性。
4.2 瑞利参数与众数和均值的比较图 11给出了BPNN、LSTM和SVR模型为分别引入瑞利参数、众数和均值作为输入特征进行波高预测的结果。可见, 在BPNN模型和LSTM模型预测中瑞利参数的预测结果的相关性R除了1 h预测, 其他时段都优于众数和均值, 而在BPNN模型中均方根误差RMSE仅在1 h的预测中高于均值, 其他时段都为最小, 在LSTM模型1 h和6 h的预测中均方根误差RMSE仅高于均值, 其他时段为最小值, 再次论证了在短期预测中瑞利参数对BPNN模型和LSTM模型的预测提高不显著。SVR模型中众数的预测结果在全时段处于最差的位置, 而瑞利参数和均值在全时段的预测结果中有高有低, 没有明显优劣势。综上, 瑞利参数在机器学习算法中, 有效性高于众数和均值。
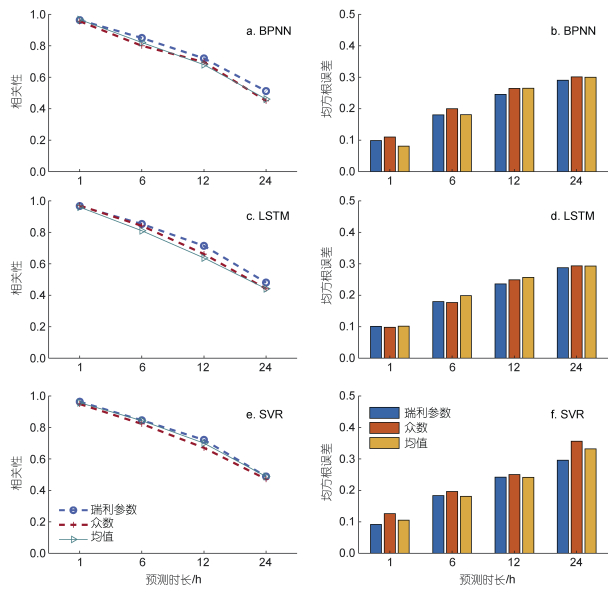 |
| 图 11 BPNN(a~b)、LSTM (c~d)和SVR (e~f)模型分别引入瑞利参数、众数和均值后的预测结果 Fig. 11 BPNN model (a~b), LSTM model (c~d), and SVR model (e~f) with the introduction of Rayleigh parameter, mode, and mean, respectively 注: a, c, e是预测结果的相关性; b, d, f预测结果的均方根误差 |
从上文的研究结果可以看出, 机器学习模型对波高预测效果只在短期(1)预报有显著的效果, 随着预报时间的增加, 效果都在显著的降低, 尤其对高海况的预报误差显著增大。影响波高的因素有风速、风向、大气压强、地形以及风区长度等, 本研究中选择了风速、风向和大气压强对波高进行预测。而对近岸海域, 风区长度和周边地形的影响往往起着至关重要的作用。这里尝试引入当地气压与区域环境气压平均值的差, 气压差与风速、风向的信息相结合, 能够一定程度上反映风区长度和地形的影响。区域环境气压平均值数据来源于欧洲中期天气预报中心(European Centre for Medium-Range Weather Forecasts, ECMWF)的第五代全球气候再分析数据集(ECMWF Reanalysis v5, ERA5)。图 12给出了以当前时刻波高、气压差与风速、风向为输入特征的波高预测结果, 从上到下依次为BPNN模型(a~d)、LSTM模型(e~h)和SVR模型(i~l)的预测结果, 从左到右依次为1、6、12和24 h的预测结果。可见, 在1、6 h的预测中三种模型引入气压差之后变化不显著, 相关性变化不超过0.01, 均方根误差变化不超过0.01 m。在12 h的预测中, BPNN模型和LSTM模型预测结果的相关性提升了0.01和0.03, 均方根误差降低了0.02 m和0.04 m。SVR模型预测结果相关性下降了0.01, 均方根误差保持不变。在24 h的预测中, 三种模型的预测结果的相关性提升了0.01~0.05, 均方根误差均降低了0.03 m。由此可见, 当地气压与区域环境气压平均值的差相比于气压本身能更好地描述近岸特征, 对中长期的波高预报具有促进作用。但是高海况的预报误差较大的问题还没有有效解决, 中长期的预测中特征选择还有待研究。此外, 本研究使用的波高数据精度较低(0.1 m), 未来应尝试更高精度数据, 以降低误差。
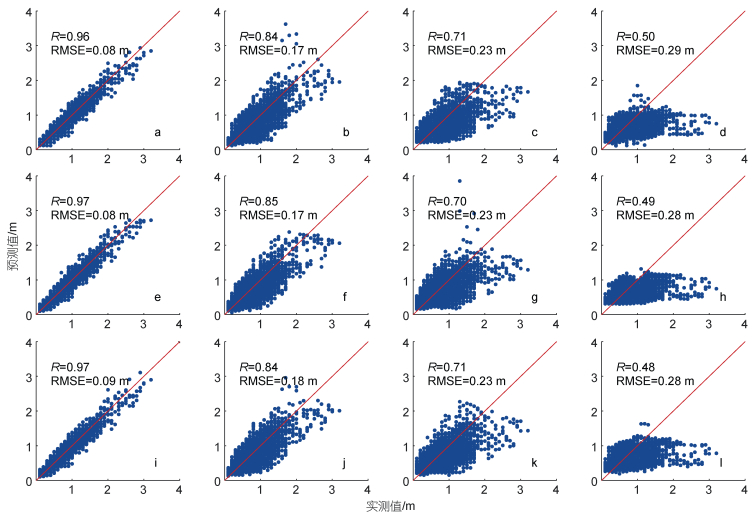 |
| 图 12 BPNN模型(a~d)、LSTM模型(e~h)和SVR模型(i~l)在1 h (a, e, i)、6 h (b, f, j)、12 h(c, g, k)和24 h (d, h, l)的预测时间范围内预测的波高与观测值之间的比较 Fig. 12 The comparison between the predicted wave heights and the observed values within the forecasting time ranges of 1 h (a, e, i), 6 h (b, f, j), 12 h (c, g, k) and 24 h (d, h, l) for the BPNN models (a~d), LSTM models (e~h) and SVR models (i~l) |
机器学习模型中数据集的划分是决定模型精度的关键因素。本研究选取2015年7月~2017年12月共29个月的观测数据为训练集, 2018年7月~2020年8月共25个月的数据为验证集, 2020年11月~2022年6月共19个月的数据为测试集。训练集长度略大于验证集和测试集。为探究训练集数据长度对模型精度影响, 这里以BPNN模型为例, 分析24个月、36个月和48个月三种不同长度训练集下的波高预测。测试集长度不变, 仍为2020年11月~2022年6月共19个月。图 13给出了BPNN模型在不同训练集长度下的波高预测结果。可见, 当训练集长度减少为24个月时(a~d), 尽管RMSE没有发生改变, 但1、12和24 h预测的相关系数R相比相比29个月训练结果(图 6e~6h)分别下降了0.01、0.01和0.03。当训练集长度增加为36个月(e~h)和48个月(i~l)时, 模型的预测效果与前文实验效果(图 6e~6h)相当, 只有训练集长度为36个月时的24 h预测中RMSE下降了0.01 m。可见, 29个月的训练集足以保障预测效果。鉴于观测数据实际情况和LSTM模型对数据连续性要求, 本文选择训练集为29个月。
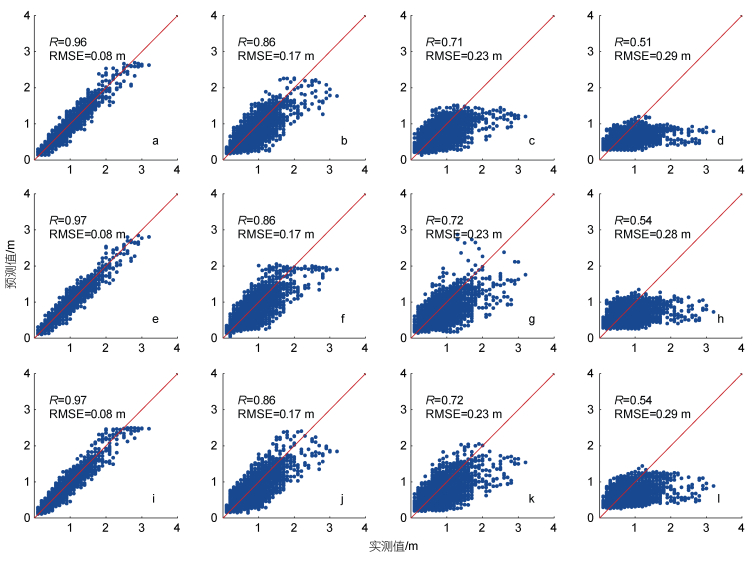 |
| 图 13 BPNN模型在训练集长度为24个月(a~d)、36个月(e~h)和48个月(i~l)时预测波高与观测值的比较 Fig. 13 Comparison between the observed and predicted wave heights derived from the BPNN model with 24-month (a~d), 36-month (e~h), and 48-month (i~l) training dataset 注: (a, e, i)、(b, f, j)、(c, g, k)和(d, h, l)分别为1h、6h、12h和24h的预测时长 |
本文运用BPNN、LSTM和SVR三种常见的机器学习模型, 对山东小麦岛观测站的实测波高数据的变化规律进行了智能预报。同时, 在运用机器学习模型对波高数据建模预测时, 引入波高分布的瑞利参数, 并与未引入瑞利参数时的预测结果进行对比分析, 发现瑞利参数有助于提升BPNN和LSTM在12和24 h中长期预报效果。实验结果表明:
(1) 在全时段的预测中SVR模型表现稍微优于BPNN和LSTM模型, 引入瑞利参数之后, 在1 h和6 h的预测中各模型的预测结果的相关性提升不超过0.02, 均方根误差的降低不超过0.01 m; 在12 h和24 h的预测中, BPNN模型和LSTM模型在引入瑞利参数之后, 预测结果相关性提升超过0.03, 均方根误差至少降低了0.02 m, 而SVR模型在12 h的预测中, 相关性提升了0.01, 均方根误差没有发生变化, 在24 h的预测中, 相关性提升了0.03, 均方根误差降低了0.01 m。引入瑞利参数之后BPNN和LSTM模型在12 h和24 h预测的效果明显得到提升, 而SVR模型在引入瑞利参数之后预测结果变化不显著。
(2) 在引入瑞利参数之前, 三种预测模型在12 h和24 h的预测中预测结果总体偏小, 而引入瑞利参数后预测结果偏小的情况得到一定程度上的减弱, 其中在BPNN和LSTM模型的12 h和24 h的预测中, 预测结果的MAE至少下降了0.02 m, 而在SVR模型的12 h和24 h的预测中, 预测结果的MAE分别下降了0 m和0.01 m, 说明瑞利参数一定程度上捕捉到了波高的变化趋势。
(3) 对模型输入的风速、风向、气压、瑞利参数4个特征进行特征扰动, 发现随着预测时长在增加, 对瑞利参数进行扰动后的误差占比增大。最后对瑞利参数、众数和均值进行对比分析, 模型输入端分别引入众数、均值和瑞利参数, 实验结果表明引入瑞利参数时预测结果优于引入众数和均值时的预测结果, 尤其是在中长期预测中。
在本文采用的机器学习算法中引入瑞利参数较大地提升了它在中长期预测效果, 可以使原机器学习模型预测的时间容许范围最大, 因此瑞利参数在海洋数值预测中具有一定的应用潜力。
致谢 感谢郑全安教授的指导和审稿人的意见。感谢国家科技资源共享服务平台—国家海洋科学数据中心(http://mds.nmdis.org.cn/)提供数据支撑。
刘子怡, 王宇嘉, 孙福禄, 等, 2022. 结合特征扰动与分配策略的集成辅助多目标优化算法[J]. 计算机工程, 48(6): 115-123. |
李自立, 蒙素素, 2022. 基于LSTM-ResNet模型的定点有效波高预测[J]. 海洋预报, 39(2): 80-85. |
李海涛, 孙亚男, 付建浩, 2022. RF-BiLSTM神经网络在海浪预测中的应用[J]. 计算机系统应用, 31(6): 331-338. |
张振全, 李醒飞, 杨少波, 2021. 基于AR-SVR模型的有效波高短期预测[J]. 太阳能学报, 42(7): 15-20. |
张鑫, 杨明华, 2008. 基于城郊环境下Okumura-Hata预测模型的校正与实现[J]. 通信技术, 41(5): 67-68, 78. |
陈水利, 李敬功, 王向公, 2005. 模糊集理论及其应用[M]. 北京: 科学出版社, 175-182.
|
陈希, 沙文钰, 李妍, 等, 2002. 人工神经网络技术在海浪预报中的应用[J]. 海洋通报, 21(2): 11-15. |
周志华, 2016. 机器学习[M]. 北京: 清华大学出版社, 133-140.
|
孟雷, 闻斌, 姜洪峰, 等, 2010. 神经网络方法对海浪有效波高数值模拟的改进[J]. 海洋预报, 27(2): 8-14. |
梁小力, 王毅, 2015. 基于SWAN模式的全球有效波高数值预报结果之初步验证[J]. 海洋预报, 32(6): 1-9. |
ASUERO A G, SAYAGO A, GONZÁLEZ A G, 2006. The correlation coefficient: an overview[J]. Critical Reviews in Analytical Chemistry, 36(1): 41-59. DOI:10.1080/10408340500526766 |
BLUM A L, LANGLEY P, 1997. Selection of relevant features and examples in machine learning[J]. Artificial Intelligence, 97(1/2): 245-271. |
CHAKRABORTY K, MEHROTRA K, MOHAN C K, et al, 1992. Forecasting the behavior of multivariate time series using neural networks[J]. Neural Networks, 5(6): 961-970. DOI:10.1016/S0893-6080(05)80092-9 |
DEO M C, JHA A, CHAPHEKAR A S, et al, 2001. Neural networks for wave forecasting[J]. Ocean Engineering, 28(7): 889-898. DOI:10.1016/S0029-8018(00)00027-5 |
DEO M C, NAIDU C S, 1998. Real time wave forecasting using neural networks[J]. Ocean Engineering, 26(3): 191-203. DOI:10.1016/S0029-8018(97)10025-7 |
DIXIT P, LONDHE S, 2016. Prediction of extreme wave heights using neuro wavelet technique[J]. Applied Ocean Research, 58: 241-252. DOI:10.1016/j.apor.2016.04.011 |
DUAN W Y, HAN Y, HUANG L M, et al, 2016. A hybrid EMD-SVR model for the short-term prediction of significant wave height[J]. Ocean Engineering, 124: 54-73. DOI:10.1016/j.oceaneng.2016.05.049 |
ELBISY M S, 2015. Sea wave parameters prediction by support vector machine using a genetic algorithm[J]. Journal of Coastal Research, 31(4): 892-899. |
ETEMAD-SHAHIDI A, MAHJOOBI J, 2009. Comparison between M5′ model tree and neural networks for prediction of significant wave height in Lake Superior[J]. Ocean Engineering, 36(15/16): 1175-1181. |
FAN S T, XIAO N H, DONG S, 2020. A novel model to predict significant wave height based on long short-term memory network[J]. Ocean Engineering, 205: 107298. DOI:10.1016/j.oceaneng.2020.107298 |
FORRISTALL G Z, 1978. On the statistical distribution of wave heights in a storm[J]. Journal of Geophysical Research: Oceans, 83(C5): 2353-2358. DOI:10.1029/JC083iC05p02353 |
GE M, KERRIGAN E C, 2016. Short-term ocean wave forecasting using an autoregressive moving average model [C] // 2016 UKACC 11th International Conference on Control (CONTROL). Belfast: IEEE: 1-6.
|
HASSELMANN K, BARNETT T P, BOUWS E, et al, 1973. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP) [J]. Ergänzungsheft zur Deutschen Hydrographischen Zeitschrift, Reihe A, Nr. 12.
|
Hinton G, Vinyals O, Dean J, 2015. Distilling the Knowledge in a Neural Network[J]. Computer Science, 14(7): 38-39. |
JAIN P, DEO M C, 2006. Neural networks in ocean engineering[J]. Ships and Offshore Structures, 1(1): 25-35. DOI:10.1533/saos.2004.0005 |
JAIN P, DEO M C, LATHA G, et al, 2011. Real time wave forecasting using wind time history and numerical model[J]. Ocean Modelling, 36(1/2): 26-39. |
JAMES S C, ZHANG Y S, O'DONNCHA F, 2018. A machine learning framework to forecast wave conditions[J]. Coastal Engineering, 137: 1-10. DOI:10.1016/j.coastaleng.2018.03.004 |
LIN J G, 2000. Parameter estimations of Rayleigh distribution[J]. Chinese Quarterly Journal of Mathematics, 15(4): 49-54. |
LIONELLO P, MALGUZZI P, BUZZI A, 1998. Coupling between the atmospheric circulation and the ocean wave field: an idealized case[J]. Journal of Physical Oceanography, 28(2): 161-177. DOI:10.1175/1520-0485(1998)028<0161:CBTACA>2.0.CO;2 |
LONGUET-HIGGINS M S, 1952. On the statistical distribution of the heights of sea waves[J]. Journal of Marine Research, 11(3): 245-266. |
LUNDBERG S M, ERION G, CHEN H, et al, 2020. From local explanations to global understanding with explainable AI for trees[J]. Nature Machine Intelligence, 2(1): 56-67. DOI:10.1038/s42256-019-0138-9 |
LUNDBERG S M, ERION G G, LEE S I, 2018. Consistent individualized feature attribution for tree ensembles [J]. arXiv preprint arXiv: 1802.03888.
|
LUNDBERG S M, LEE S I, 2017. A unified approach to interpreting model predictions [C]//Proceedings of the 31st International Conference on Neural Information Processing Systems. Long Beach: Curran Associates Inc. : 4768-4777.
|
MAHJOOBI J, MOSABBEB E A, 2009. Prediction of significant wave height using regressive support vector machines[J]. Ocean Engineering, 36(5): 339-347. DOI:10.1016/j.oceaneng.2009.01.001 |
MAKARYNSKYY O, 2004. Improving wave predictions with artificial neural networks[J]. Ocean Engineering, 31(5/6): 709-724. |
OUYANG L, LING F H, LI Y, et al, 2023. Wave forecast in the Atlantic Ocean using a double-stage ConvLSTM network[J]. Atmospheric and Oceanic Science Letters, 16(4): 100347. DOI:10.1016/j.aosl.2023.100347 |
QI Y T, ZHOU Z N, YANG L L, et al, 2019. A decomposition- ensemble learning model based on LSTM neural network for daily reservoir inflow forecasting[J]. Water Resources Management, 33(12): 4123-4139. DOI:10.1007/s11269-019-02345-1 |
The Swamp Group, 2013. Ocean Wave Modeling[M]. New York: Springer.
|
TSAI C P, LIN C, SHEN J N, 2002. Neural network for wave forecasting among multi-stations[J]. Ocean Engineering, 29(13): 1683-1695. DOI:10.1016/S0029-8018(01)00112-3 |
WANG W X, TANG R C, LI C, et al, 2018. A BP neural network model optimized by Mind Evolutionary Algorithm for predicting the ocean wave heights[J]. Ocean Engineering, 162: 98-107. DOI:10.1016/j.oceaneng.2018.04.039 |
WANG J C, ZHANG J, YANG J G, et al, 2017. An evaluation of input/dissipation terms in WAVEWATCH Ⅲ using in situ and satellite significant wave height data in the South China Sea[J]. Acta Oceanologica Sinica, 36(3): 20-25. DOI:10.1007/s13131-017-1038-7 |
WILSON B W, 1965. Numerical prediction of ocean waves in the North Atlantic for December, 1959[J]. Deutsche Hydrografische Zeitschrift, 18(3): 114-130. DOI:10.1007/BF02333333 |
ZHOU T, LU H L, WANG W W, et al, 2019. GA-SVM based feature selection and parameter optimization in hospitalization expense modeling[J]. Applied Soft Computing, 75: 323-332. DOI:10.1016/j.asoc.2018.11.001 |
ZHU Y C, ZHANG R H, MOUM J N, et al, 2022. Physics- informed deep-learning parameterization of ocean vertical mixing improves climate simulations[J]. National Science Review, 9(8): nwac044. DOI:10.1093/nsr/nwac044 |
 2024, Vol. 55
2024, Vol. 55


