
中国海洋湖沼学会主办。
文章信息
- 马启良, 刘梅, 祁亨年, 杨小明, 原居林. 2024.
- MA Qi-Liang, LIU Mei, QI Heng-Nian, YANG Xiao-Ming, YUAN Ju-Lin. 2024.
- 基于CSA-PLS算法的养殖水体水质快速高光谱预测反演模型研究
- FAST HYPERSPECTRAL PREDICTION AND INVERSION MODEL OF AQUACULTURE WATER QUALITY BASED ON CSA-PLS ALGORITHM
- 海洋与湖沼, 55(2): 375-385
- Oceanologia et Limnologia Sinica, 55(2): 375-385.
- http://dx.doi.org/10.11693/hyhz20231100245
文章历史
-
收稿日期:2023-11-16
收修改稿日期:2024-01-16
2. 湖州师范学院信息工程学院 浙江湖州 313000;
3. 浙江省淡水水产研究所 浙江湖州 313001
2. School of Information Engineering, Huzhou University, Huzhou 313000, China;
3. Zhejiang Institute of Freshwater Fisheries, Huzhou 313001, China
淡水池塘养殖在我国起步较早, 历史悠久, 但由于工业化水平低, 技术更新慢, 在高速发展的现代渔业中已凸显不足; 而淡水池塘在保障我国优质蛋白供给、促进渔民增收等方面发挥着重要的作用, 近年来以绿色发展为引领, 不断推进全国现代渔业高质量发展, 渔业经济总产值稳步提高, 水产品品质不断提升(刘亚迪等, 2020)。在这一发展过程中, 池塘养殖水环境的数字化采集、智能化管控以及实时预警调控是实现渔业现代化的关键, 而养殖水环境各水质参数的快速准确获取是智能化管控和实时预警调控的前提必备条件。目前养殖水环境的悬浮物浓度、叶绿素a、总磷、总氮、氨氮、化学需氧量等参数指标监测, 仍采用常规的水质监测方法, 即对水体进行定期、定点采样及实验室内水质检测。由于受人力、物力以及时间和天气等限制, 人工采集的数据量有限, 且成本高、速度慢; 这些采样点检测后只能体现局部水质状况, 无法快速获取整个养殖小区内所有池塘水域的水质参数变化和空间分布情况, 不能有效达到养殖水质实时预警调控要求, 因此迫切需要一种能快速、实时和大尺度的监测方法。
水体光谱特征在快速获取水质状况和时空变化趋势上有着独特的优势(Feng et al, 2014; 李鑫星等, 2018), 因此遥感水质监测方法被广泛用于湖泊、水库、河道等内陆水体的研究上, 但大多针对叶绿素a和悬浮物等具有光学活性的物质, 且研究已较为成熟(Liu et al, 2018; 殷子瑶等, 2021); 而对于其他非光学活性的物质, 如总氮、氨氮、总磷、化学需氧量、高锰酸钾指数等, 由于没有直接的光学特性, 无法进行直接的遥感反演, 往往需要借助水体中不同物质之间的关系进行遥感反演, 相关研究较少, 且精度相对较低(马丰魁等, 2020; 刘轩等, 2021)。近几年, 随着无人机和高光谱技术的成熟, 使得高光谱遥感得到了很多研究者的青睐, 杨振等(2020)利用机载高光谱技术建立了矿区水库高光谱影像和悬浮物、浊度的反演模型, 陈俊英等(2019)建立了基于地物高光谱污水处理厂水质综合评价方法, 黄宇等(2020)利用无人机高光谱成像技术对河湖水质悬浮物、浊度、总氮、总磷和叶绿素a进行了预测反演, Cook等(2023)利用高光谱数据对叶绿素a和藻蓝蛋白数据进行预测反演并进一步研究构建了蓝藻水华方面的预测模型, 陈仲锴等(2021)利用高光谱对茅洲河悬浮物浓度进行了反演研究, 都取得了较好的预测效果。但面对高光谱数据量大、自变量高共线性等特点, 导致使用全波段构建的水质参数反演模型存在建模效率低、计算量大、模型结构复杂, 以及使用相关性较高波段构建模型存在普适性和稳定性较差等问题, 尤其是对池塘养殖水体这种小微水体的适用性值得更进一步探究。
因此, 如何筛选有效波长是构建稳健高光谱水质反演模型的关键问题, 目前已有的高光谱波段筛选方法主要有遗传算法(GA)、无信息变量消除法(UVE)、竞争性自适应重加权算法(CARS)、连续投影算法(SPA)等(于雷等, 2016)。鉴于此, 针对当前实际采集水体样本数量少以及高光谱数据量大的现实, 提出了一种乌鸦搜索算法(Crow Search Algorithm, CSA)结合偏最小二乘回归模型(Partial Least Squares Regression, PLSR)的高光谱特征波段自动筛选方法, 并将算法自动筛选的特征波段分别作为支持向量回归(Support Vector Regression, SVR)和自适应增强(Adaptive Boosting, AdaBoost)回归模型的输入因子, 训练养殖水体各水质参数的预测反演模型, 与全波段和连续投影算法(SPA)筛选波段后构建的模型进行比较分析, 最后用验证集对模型的稳定性和准确性进行验证和比较, 以期为池塘养殖水环境各水质参数的快速监测及实时调控提供理论基础与技术依据。
1 实验数据与方法 1.1 研究区域及数据获取研究区域为浙江省湖州市杨港村现代生态渔业园内, 所选天气均为晴朗、微风, 适于实验人员开展水体采样和高光谱影像拍摄工作。具体采样点位分布如图 1所示, 采集水体样本49份, 并将水体样本送至专业水质分析机构对水质参数TN、NH4+-N、TP和COD分别进行测定, 其测定值作为参考值。高光谱影像的拍摄利用大疆六旋翼无人机M600 Pro, 并搭载高光谱成像光谱仪GaiaSky-mini-2, 无人机高光谱相机的光谱扫描范围为400~1 000 nm, 光谱通道数为176, 光谱分辨率为3.5 nm。拍摄完成后利用设备自带软件对高光谱影像进行预处理, 包括镜像变换、黑白帧校正、大气校正、几何校正及图像的拼接等。
 |
| 图 1 研究区域和规划的采样点分布情况 Fig. 1 The study area and Distribution of sampling points |
由于养殖池面积一般小于1 ha, 水深在2 m范围内, 养殖池中心和岸边的水质要素差异并不显著, 具有均一性特点。因此, 采样点处光谱反射率数据的提取, 依据实际采样点位置, 在高光谱影像上分别构建以采样点为中心的7×7矩阵作为感兴趣区域(Region of Interest, ROI), 以区域内所有光谱点的平均光谱反射率值作为该采样点的光谱反射率数据(赵凡等, 2016), 共获得49组与实验室检测数据相对应的光谱反射率数据。
1.2 数据集划分为增加训练和验证数据集划分的合理性, 利用化学计量学中的经典算法SPXY (Sample set Partitioning based on joint X-Y distance) (马启良等, 2022)实现数据集的划分, SPXY既考虑X光谱空间对训练集选取的影响, 同时也考虑Y浓度矩阵对训练集选取的影响, 基于X-Y联合距离对样本集进行选取, 训练集和验证集的划分比例为4︰1。
1.3 光谱曲线特征及数据预处理由于拍摄设备及环境的影响, 光谱数据难免会混有噪声, 为减少噪声对分析结果的影响, 首先利用卷积平滑算法(Savitzky Golay, SG)对采样点光谱数据进行预处理, 接着利用一阶导数(First Derivative, D1)、对数(Logarithmic, LOG)、小波变换(Wavelet Transform, WT)以及标准正态变换(Standard Normal Variate, SNV)对光谱数据进一步处理。采样点原始光谱数据以及处理后的光谱数据对应的曲线特征如图 2所示。其中图 2a为原始光谱数据的曲线特征, 图 2b为经过SG算法处理后的光谱曲线特征, 图 2c~图 2f分别为经过D1、LOG、WT和SNV处理后的光谱曲线特征。
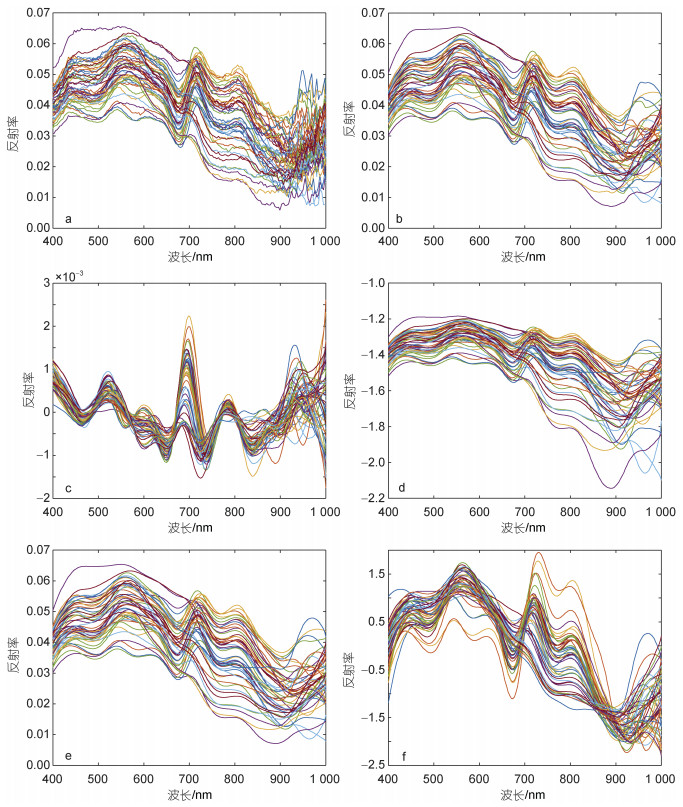 |
| 图 2 采样点光谱反射率曲线及预处理结果 Fig. 2 Spectral reflectance curves of sampling points and preprocessing results 注: a. 原光谱曲线; b. SG平滑; c.一阶导数; d. 对数; e. 小波变换; f. 标准正态变换 |
从图 2a的曲线变换规律上看, 存在明显的双峰特征, 分别在500~600 nm区间和680~750 nm区间, 表明水体的浮游藻类比较丰富(王林等, 2022)。在570 nm绿光波段附近出现第一峰值, 在720 nm红光波段附近出现第二峰值, 有“红移现象”出现(陈涛等, 1994; 陈点点等, 2022), 是典型的内陆水体特征, 均由水体中藻类和悬浮物的强反射作用引起的(Gitelson et al, 1993)。不同养殖水体区域光谱曲线总体趋势一致, 仅光谱的反射强度存在一定差异, 这与不同区域水质参数的浓度含量差异相对应。
1.4 CSA-PLS的特征波段自动筛选方法乌鸦搜索算法(CSA)由Askarzadeh在2016年提出(Askarzadeh, 2016), 用于解决约束工程优化问题, 是一种全局优化算法, 模拟一群乌鸦觅食的智能行为。CSA算法主要涉及的参数有种群大小N, 问题维度Q, 飞行步长FL, 最大迭代次数MaxIter, 还有种群的初始位置C及存储食物的记忆位置M。本文将其应用于特征波段的自动筛选上, 初始化参数N为20, Q设置为波段总数176, FL设置为1, MaxIter设置为176保证遍历到每个光谱波段。利用SG处理后的光谱数据与实测值进行Pearson相关性分析, 并根据相关系数大小对光谱波段进行由大到小排序, 选择前N个最大相关系数对应的波段编号分别对位置C和M进行初始化, 目标函数设置为预测值和实测值的均方根误差RMSE, 根据RMSE值大小判断当前加入的波段是否保留, 直至迭代完成。在迭代筛选波段过程中, 模型的训练基于Python的Sklearn机器学习库的, 并充分利用GridSearchCV函数的网格搜索和交叉验证功能, 以保证模型的鲁棒性。CSA-PLS的自动波段筛选方法流程如图 3所示。另外, 为了快速构建基于CSA-PLS方法的回归模型, 将CSA-PLS光谱特征波段筛选方法与传统机器学习方法结合, 只需输入样本的光谱特征和实测水质参数数据, 就可自动快速筛选出特征波段, 实现模型的构建和水质参数的预测反演。为验证所提方法构建预测模型的有效性, 分别与全波段预测模型和SPA筛选的特征波段预测模型进行了对比分析, 更加清晰的呈现了该方法的预测效果。
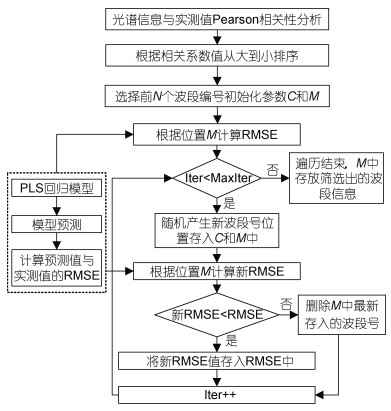 |
| 图 3 CSA-PLS算法自动波段筛选方法流程图 Fig. 3 The flowchart of CSA-PLS algorithm for automatic band selection |
根据预处理后的光谱数据和筛选出的特征光谱, 选择了支持向量回归(SVR)和集成学习(AdaBoost)两种回归模型对光谱特征数据分别进行建模分析, 最后根据模型的相关评价标准筛选出各水质参数的最佳反演模型。SVR和AdaBoost的基本原理如下:
SVR是一种基于支持向量机(SVM)的回归方法。与传统的线性回归方法不同, SVR试图找到一个函数, 该函数在输入空间中将样本点映射到高维特征空间, 以最大程度地减小预测误差, 它的目标是找到一个边界(支持向量), 使得落在边界内的样本点的预测误差最小, 同时保持边界内外的点的误差小于某个容忍度。SVR也可以处理非线性关系, 具有较好的泛化能力, 并且对异常值不敏感。
AdaBoost作为一种集成学习方法, 主要用于改进弱回归模型的性能, 首先, 训练一个基础回归模型, 然后根据其预测误差来调整每个样本的权重。接下来, 再训练另一个回归模型, 重复这个过程, 不断更新样本权重, 使之前被误分类的样本更加受关注。最终, AdaBoost将多个弱模型组合成一个强回归模型, 通过加权组合它们的预测结果来进行回归。可以提高回归模型的性能, 通常对参数不敏感, 不容易过拟合。
1.6 模型评价指标为了验证模型的优劣, 从预测值和实测值之间的决定系数(Coefficient of Determination, R2)和均方根误差(Root Mean Square Error, RMSE)来进行分析评价, 公式分别如式(1)和式(2)所示。决定系数用来衡量模型的好坏, 评价标准为R2≥0.91为精准, 0.82≤ R2≤0.9为较好, 0.66≤R2≤0.81为一般, 0.50≤R2≤ 0.65为较差; 均方根误差用来评价预测值与实测值的接近程度, RMSE越小预测值与实测值越接近。
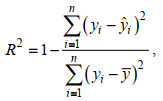 (1)
(1)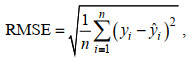 (2)
(2)其中, y和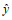
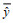
各水质指标与光谱波段相关系数曲线如图 4所示, 可以发现相关系数的总体变化趋势是一致的, 各水质指标最大相关波段均在波长700~900 nm区间内, TP和COD均在波长720 nm附近达到了峰值, 最大相关系数分别为0.765和0.674; TN和NH4+-N的整体相关性较弱, 分别在710 nm和680 nm附近达到峰值, 最大相关系数分别为0.375和0.485。
 |
| 图 4 各水质指标与光谱反射率值的相关系数曲线 Fig. 4 The correlation coefficient curves between each water quality indicator and spectral reflectance values |
水质指标TN、NH4+-N、TP和COD利用CSA-PLS和SPA算法自动筛选光谱特征波段结果如图 5所示, 从图 5可知, 4种水质指标提取的波段主要集中在450~900 nm之间, 而小于450 nm和大于900 nm的光谱波段筛选的很少, 这主要由于该波长区间的光谱反射率更易受外界条件及仪器设计误差等因素的影响, 信噪比低(陈俊英等, 2019; 黄华等, 2021); 700~ 900 nm范围是相关系数最强的区间, 而从两种筛选方法的结果上看, 并不都集中在最相关区间里; 400~ 700 nm范围相关系数较低的区间也有被筛选到的波段; 尤其是水质指标NH4+-N在整个波长区间都有波段被筛选。这进一步证明了水质参数的差异不仅仅体现在最相关的个别波段上, 而体现在可见光到近红外光谱反射率的所有波段上, 其他相关性较低的波段对水质参数的影响也不可忽视(段洪涛等, 2006), 对水质预测模型准确率的提高同样是有贡献的。
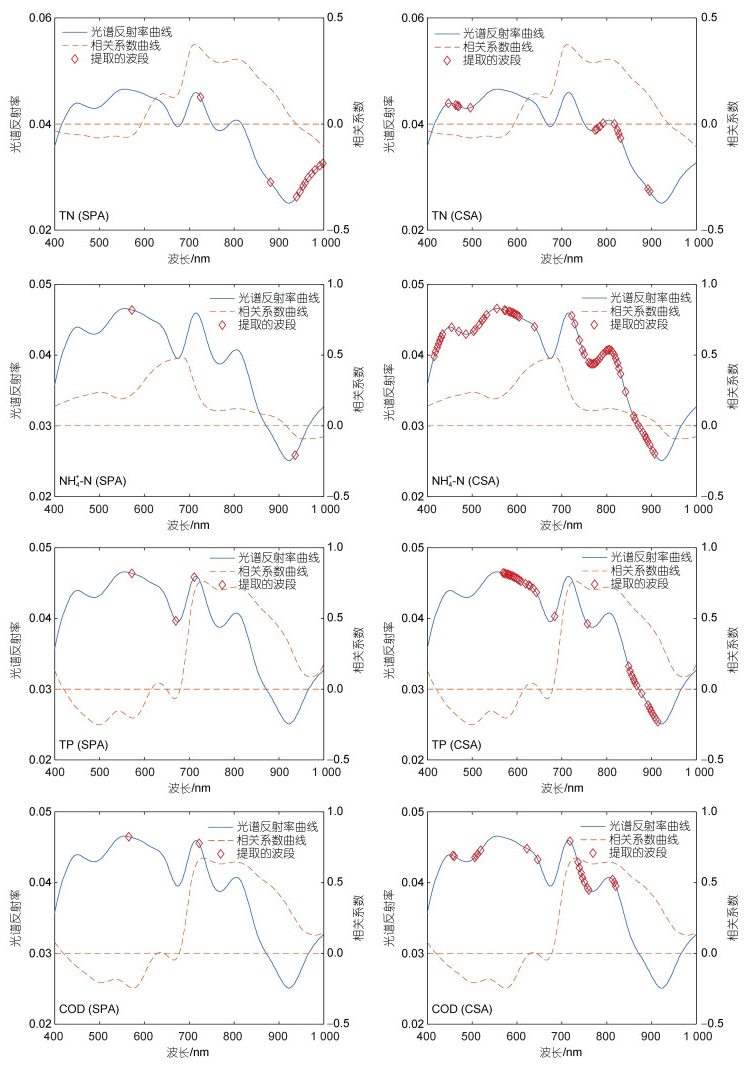 |
| 图 5 各水质指标对应SPA和CSA算法的光谱特征波段筛选结果 Fig. 5 The spectral feature band selection results for each water quality indicator using SPA and CSA algorithms |
采样点原始光谱数据经过不同预处理方法处理后, 分别训练SVR和AdaBoost模型, 并对测试集进行预测, 同时计算各水质指标预测结果和实测值的决定系统R2和均方根误差RMSE。各水质指标对应不同预处理方法的全波段模型预测评价结果如表 1所示。
| 指标 | 模型 | 评价指标 | 预处理方法 | |||||
| RAW | SG | D1 | LOG | WT | SNV | |||
| TN | FB-SVR | R2 | 0.342 | 0.535 | 0.189 | 0.031 | 0.533 | 0.026 |
| RMSE | 0.702 | 0.587 | 0.775 | 0.847 | 0.588 | 0.849 | ||
| FB-AdaBoost | R2 | 0.059 | –0.238 | –0.654 | –0.012 | –0.017 | –0.398 | |
| RMSE | 0.839 | 0.957 | 1.107 | 0.865 | 0.868 | 1.018 | ||
| NH4+-N | FB-SVR | R2 | –0.01 | 0.464 | –0.146 | –0.904 | 0.464 | –11.948 |
| RMSE | 0.43 | 0.312 | 0.458 | 0.59 | 0.313 | 1.539 | ||
| FB-AdaBoost | R2 | 0.621 | 0.169 | 0.551 | 0.154 | 0.201 | 0.433 | |
| RMSE | 0.263 | 0.389 | 0.286 | 0.393 | 0.382 | 0.321 | ||
| TP | FB-SVR | R2 | 0.61 | 0.611 | 0.547 | 0.612 | 0.609 | 0.631 |
| RMSE | 0.08 | 0.081 | 0.087 | 0.081 | 0.081 | 0.078 | ||
| FB-AdaBoost | R2 | 0.853 | 0.68 | 0.609 | 0.717 | 0.731 | 0.682 | |
| RMSE | 0.049 | 0.073 | 0.081 | 0.068 | 0.067 | 0.072 | ||
| COD | FB-SVR | R2 | 0.018 | 0.302 | –0.012 | 0.351 | 0.302 | 0.547 |
| RMSE | 18.978 | 15.994 | 19.269 | 15.432 | 15.994 | 12.891 | ||
| FB-AdaBoost | R2 | 0.347 | 0.431 | 0.501 | 0.361 | 0.325 | 0.699 | |
| RMSE | 15.468 | 14.451 | 13.529 | 15.311 | 15.729 | 10.496 | ||
从表 1中可以看出, 在全波段构建的模型中, TN经过SG平滑处理后的FB-SVR模型的预测效果最好, R2和RMSE分别为0.535和0.587; NH4+-N在原始光谱数据下的FB-AdaBoost模型预测效果最好, R2和RMSE分别为0.621和0.263; TP在原始光谱数据下的FB-AdaBoost模型的预测效果最好, R2和RMSE分别为0.853和0.049; COD在标准正态变换后的FB-AdaBoost模型预测效果最好, R2和RMSE分别为0.699和10.496。
2.4 CSA-PLS和SPA模型及光谱预处理方法比较用CSA-PLS和SPA算法筛选出关键波段组合, 结合不同的预处理方法得到光谱数据, 将其作为SVR和AdaBoost模型的输入, 训练模型并对测试集进行预测, 各水质指标对应的模型预测结果与实测值的决定系数和均方根误差值如表 2所示。
| 指标 | 模型 | 评价指标 | 预处理方法 | |||||
| RAW | SG | D1 | LOG | WT | SNV | |||
| TN | CSA-SVR | R2 | 0.358 | 0.335 | 0.002 | 0.419 | 0.334 | 0.477 |
| RMSE | 0.693 | 0.705 | 0.864 | 0.659 | 0.706 | 0.625 | ||
| CSA-AdaBoost | R2 | –0.096 | –0.125 | 0.633 | –0.314 | –0.187 | –0.066 | |
| RMSE | 0.906 | 0.918 | 0.524 | 0.992 | 0.943 | 0.894 | ||
| SPA-SVR | R2 | 0.343 | 0.351 | 0.003 | 0.248 | 0.352 | –0.447 | |
| RMSE | 0.701 | 0.697 | 0.864 | 0.75 | 0.696 | 1.041 | ||
| SPA-AdaBoost | R2 | –0.069 | –0.117 | –0.036 | –0.343 | –0.004 | –0.203 | |
| RMSE | 0.895 | 0.915 | 0.881 | 1.003 | 0.867 | 0.95 | ||
| NH4+-N | CSA-SVR | R2 | –2.409 | –1.073 | –2.278 | –1.433 | –1.074 | –1.245 |
| RMSE | 0.79 | 0.616 | 0.774 | 0.667 | 0.616 | 0.641 | ||
| CSA-AdaBoost | R2 | 0.061 | –0.069 | 0.525 | –0.069 | –0.148 | 0.647 | |
| RMSE | 0.414 | 0.442 | 0.294 | 0.442 | 0.458 | 0.254 | ||
| SPA-SVR | R2 | –2.112 | –2.145 | –2.255 | –0.754 | –2.144 | –2.238 | |
| RMSE | 0.754 | 0.758 | 0.772 | 0.566 | 0.758 | 0.77 | ||
| SPA-AdaBoost | R2 | –0.344 | –0.135 | 0.021 | –0.03 | –0.117 | –3.092 | |
| RMSE | 0.496 | 0.455 | 0.423 | 0.434 | 0.452 | 0.865 | ||
| TP | CSA-SVR | R2 | –0.003 | –0.003 | –0.003 | –0.003 | –0.003 | –0.003 |
| RMSE | 0.129 | 0.129 | 0.129 | 0.129 | 0.129 | 0.129 | ||
| CSA-AdaBoost | R2 | 0.615 | 0.699 | 0.556 | 0.642 | 0.698 | 0.758 | |
| RMSE | 0.08 | 0.071 | 0.086 | 0.077 | 0.071 | 0.063 | ||
| SPA-SVR | R2 | –0.003 | –0.003 | –0.003 | –0.003 | –0.003 | –0.003 | |
| RMSE | 0.129 | 0.129 | 0.129 | 0.129 | 0.129 | 0.129 | ||
| SPA-AdaBoost | R2 | 0.644 | 0.598 | 0.567 | 0.623 | 0.527 | 0.674 | |
| RMSE | 0.077 | 0.082 | 0.085 | 0.079 | 0.089 | 0.073 | ||
| COD | CSA-SVR | R2 | 0.104 | 0.258 | –0.035 | 0.407 | 0.258 | 0.527 |
| RMSE | 18.127 | 16.495 | 19.49 | 14.747 | 16.498 | 13.163 | ||
| CSA-AdaBoost | R2 | –0.281 | 0.245 | 0.704 | 0.051 | 0.353 | 0.714 | |
| RMSE | 21.684 | 16.639 | 10.414 | 18.654 | 15.399 | 10.229 | ||
| SPA-SVR | R2 | 0.045 | 0.042 | –0.036 | 0.32 | 0.042 | 0.698 | |
| RMSE | 18.709 | 18.745 | 19.496 | 15.791 | 18.747 | 10.511 | ||
| SPA-AdaBoost | R2 | 0.369 | 0.229 | –0.797 | 0.362 | 0.266 | 0.684 | |
| RMSE | 15.208 | 16.813 | 25.678 | 15.297 | 16.403 | 10.759 | ||
从表 2可以看出, 筛选波段后, TN在一阶导数变换后的CSA-AdaBoost模型取得最优预测结果; NH4+-N、TP和COD均为标准正态变换后的CSA-AdaBoost模型取得最优预测结果。可见AdaBoost模型对水质指标TN、NH4+-N、TP和COD的预测效果要优于SVR模型, 这也充分体现了集成学习AdaBoost模型在处理高光谱共线性问题中的优势, 更适合用于光谱数据的分析和处理(张杰等, 2022)。同时也可以看出, 提出的CSA-PLS光谱波段筛选方法在模型的总体预测精度上要优于传统的SPA波段筛选方法。
2.5 模型对比分析与评价从表 1与表 2预测结果的评价指标上看, 各水质指标基于全波段和SPA算法筛选的波段得到的最优模型, 预测精度总体上要弱于提出的CSA-PLS算法筛选特征波段后得到的最优模型。常规的SPA波段筛选方法在决定系数R2和均方根误差RMSE上, 相较于FB都有所降低, 而提出的CSA-PLS波段筛选方法相对FB: TN提升18.32%和10.73%; NH4+-N提升17.42%和11.19%; COD提升2.15%和2.54%; 仅TP略有降低, 说明TP浓度用全波段预测更为准确。为了比较训练集和验证集的预测值与实测值的接近程度, 选择提出的波段筛选方法CSA-PLS结合集成学习AdaBoost回归模型对TN、NH4+-N、TP和COD的训练集和验证集进行预测, 预测值与实测值的对比结果如图 6所示。
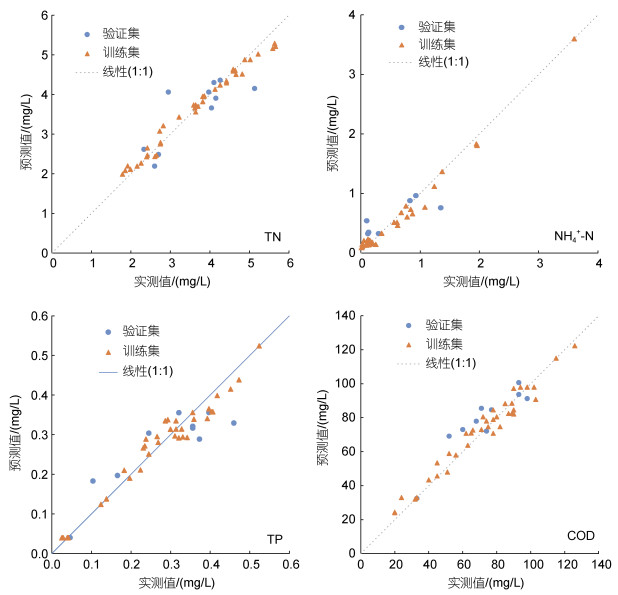 |
| 图 6 各水质指标对应CSA-AdaBoost模型的预测值与实测值对比 Fig. 6 Comparison of predicted and measured values for various water quality indicators using the CSA-AdaBoost Model |
目前, 对小微水体的水环境光谱反演研究并不多, 顾佳艳等(2022)利用高光谱技术监测化学需氧量、氨氮、总磷、叶绿素a (chl a)、总悬浮物以及透明度等参数, 构建反演模型判别黑臭水体; 刘彦君等(2019)利用无人机多光谱影像对总磷、悬浮物浓度以及浊度建立了遥感反演模型, 并构建了水域各参数的空间分布图。这些小微水体水质时空变化较小, 且大多不以指导生产为目的, 而尤其是养殖池塘水质预测主要是为了水质预警与调控, 从而保证养殖对象的正常生长, 对水质的实时性和准确性要求更高。但是养殖水体水质比这些小微水体要复杂很多(黄李童等, 2018; 刘彦君等, 2019; Guimarães et al, 2019), 因其受人为干扰更大, 如频繁地投饵、捕捞等行为, 以及高密度养殖对象的代谢及扰动行为。目前, 对养殖池塘这类小微水体水质监测方面已经有一些探索性的应用研究(黄昕晰等, 2020; 刘梅等, 2022), 如刘梅等利用6种模型开展了池塘高光谱水质预测研究, 但是该方法仅对双波段的数学变换和全波段进行了分析, 水质预测误差可进一步优化, 需从筛选更适光谱数据处理方法以有效提高养殖水体水质预测的精准度, 从而更好地指导养殖生产。高光谱遥感具有高空间分辨率、高光谱分辨率的特点, 有利于对光学特性复杂多变的小微水体进行预测反演。本文利用无人机搭载高光谱传感器, 在池塘养殖小区上空拍摄高光谱影像数据, 并结合同时期采集水体样本的水质参数实测数据, 深入分析本研究新提出的CSA-PLS算法对池塘养殖小区水体水质参数(TN、NH4+-N、TP和COD)预测准确度提升的适用性研究。
高光谱具有丰富的光谱信息, 但由于光谱采集中会带有人为和自然因素的干扰, 在反演获取水质信息前必须经过相关数据处理, 以尽可能降低光谱干扰信息(Cao et al, 2021; 陈洁等, 2023)。目前, 用来筛选有效光谱信息的方法比较多, 比较常用的有遗传算法(GA)、无信息变量消除法(UVE)、竞争性自适应重加权算法(CARS)、连续投影算法(SPA), 如Chen等(2021)利用GA和XGBoost对城市河流中的叶绿素a、总磷、总氮、氨氮和浊度进行预测, 与其他算法如随机森林、遗传算法随机森林等相比, GA-XGBoost性能更好; 姜吉光等(2023)利用SPA对水质样本的紫外吸收光谱特征波长进行筛选, 消除无关冗余数据以提高模型迭代速率和精度, 实现野外水体的化学需氧量(COD)和浊度预测等。可见, 不同的光谱处理算法及波段筛选方法, 其精度亦存在较大差距。
CSA是一种智能仿生算法, 全局优化能力强; PLS是被广泛应用的偏最小二乘分析方法, 具有多因变量对多自变量分析的优点。本研究将CSA和PLS方法进行创新性结合, 充分利用两者各自优势, 最大程度降低光谱信息重叠度和冗余度, 挖掘其隐藏的真实信息, 并同SPA方法进行比较分析, 结果显示本研究新构建的CSA-PLS算法可以有效减少池塘养殖水体光谱信息系统误差和背景噪声的影响, 进一步增强了光谱信噪比, 实现对养殖水质指标TN、NH4+-N、TP和COD进行精准反演。同时所提的波段自动筛选方法可有效对高光谱数据降维, 为解决高光谱数据量大以及光谱的共线性问题提供了一种新的方法; 结合集成学习AdaBoost构建的预测模型, 具有更好的稳定性和鲁棒性。
该模型可以快速、准确地预测反演养殖水环境水质参数, 且能够满足大尺度、重复观测的需求, 为实现养殖水体水质实时准确的在线监测和预警调控提供理论基础和技术支撑。本文仍存在一些不足, 实际采集的样本数量及对应的高光谱影像数据有限, 未来将进一步丰富样本集, 保证样本集的均衡性, 并应用于大水面(水库、湖泊等)大尺度水质的实时反演, 进一步提高模型的预测精度和普适性需求。
4 结论(1) 本研究比较分析了5种光谱预处理方法、SPA和CSA-PLS两种光谱波段筛选方法以及SVR和AdaBoost两种回归分析模型。对养殖池塘水质预测准确性, 提出的基于CSA-PLS算法的高光谱波段筛选方法结合AdaBoost的反演模型, 更适用于池塘养殖小微水体, 最大程度降低光谱信息重叠度和冗余度, 提高信噪比, 有效减少了全量光谱数据在预测反演中共线性、计算量大等问题。
(2) 基于CSA-PLS算法的养殖水体水质高光谱水质反演模型进行养殖水体水质预测结果显示, 所提波段筛选方法预测获得的TN、NH4+-N、TP和COD最优预测模型, 均优于传统的SPA波段筛选方法; 所提方法与全波段最优模型相比, 在R2和RMSE上TN提升了18.32%和10.73%; NH4+-N提升了17.42%和11.19%; COD提升了2.15%和2.54%, 预测精度可以满足了养殖户对养殖水质动态变化情况实时掌握的要求, 又起到预警调控作用, 即能够及时提示养殖户对较差水质的养殖塘进行水环境调控, 改善养殖水环境, 有效降低了养殖风险。
于雷, 洪永胜, 周勇, 等, 2016. 高光谱估算土壤有机质含量的波长变量筛选方法[J]. 农业工程学报, 32(13): 95-102. DOI:10.11975/j.issn.1002-6819.2016.13.014 |
马丰魁, 姜群鸥, 徐藜丹, 等, 2020. 基于BP神经网络算法的密云水库水质参数反演研究[J]. 生态环境学报, 29(3): 569-579. |
马启良, 原居林, 张爱华, 等, 2022. 基于无人机高光谱技术的水质预测反演系统设计与实现[J]. 湖州师范学院学报, 44(2): 56-62. |
王林, 王祥, 王新新, 等, 2022. 基于Sentinel-3 OLCI影像的秦皇岛海域悬浮物浓度遥感反演[J]. 中国环境科学, 42(8): 3867-3875. |
刘亚迪, 余连祥, 冷华南, 2020. 乡村振兴战略背景下现代渔业发展优势、问题及政策分析——以浙江省湖州市南浔区渔业发展为例[J]. 海洋湖沼通报, (5): 155-163. |
刘轩, 赵同谦, 蔡太义, 等, 2021. 丹江口水库总氮、氨氮遥感反演及时空变化研究[J]. 农业资源与环境学报, 38(5): 829-838. |
刘彦君, 夏凯, 冯海林, 等, 2019. 基于无人机多光谱影像的小微水域水质要素反演[J]. 环境科学学报, 39(4): 1241-1249. |
刘梅, 马启良, 原居林, 等, 2022. 基于无人机高光谱遥感技术对内陆养殖池塘水质监测的研究[J]. 海洋与湖沼, 53(1): 195-205. |
李鑫星, 朱晨光, 周婧, 等, 2018. 光谱技术在水产养殖水质监测中的应用进展及趋势[J]. 农业工程学报, 34(19): 184-194. |
杨振, 卢小平, 武永斌, 等, 2020. 无人机高光谱遥感的水质参数反演与模型构建[J]. 测绘科学, 45(9): 60-64, 95. |
张杰, 徐波, 冯海宽, 等, 2022. 基于集成学习的水稻氮素营养及籽粒蛋白含量监测[J]. 光谱学与光谱分析, 42(6): 1956-1964. |
陈仲锴, 厉小润, 赵辽英, 2021. 基于高光谱数据波段选择的茅洲河悬浮物浓度反演[J]. 激光与光电子学进展, 58(20): 2001001. |
陈点点, 陈芸芝, 冯险峰, 等, 2022. 基于超参数优化CatBoost算法的河流悬浮物浓度遥感反演[J]. 地球信息科学学报, 24(4): 780-791. |
陈俊英, 邢正, 张智韬, 等, 2019. 基于高光谱定量反演模型的污水综合水质评价[J]. 农业机械学报, 50(11): 200-209. |
陈洁, 张立福, 张红明, 等, 2023. 白洋淀水体总磷总氮高光谱估算模型比较[J]. 遥感学报, 27(7): 1642-1652. |
陈涛, 李武, 吴曙初, 1994. 悬浮泥沙浓度与光谱反射率峰值波长红移的相关关系[J]. 海洋学报(中文版), 16(1): 38-43. |
赵凡, 董金磊, 郭文川, 2016. 高光谱图像光谱提取区域对猕猴桃糖度检测精度的影响[J]. 现代食品科技, 32(4): 223-228. |
段洪涛, 张柏, 宋开山, 等, 2006. 长春南湖水体透明度高光谱定量模型研究[J]. 中国科学院研究生院学报, 23(5): 633-639. |
姜吉光, 石磊, 苏成志, 等, 2023. 基于SPA-SVR的紫外光谱水质污染物含量解耦预测方法[J]. 激光与光电子学进展, 60(7): 0730004. |
顾佳艳, 何国富, 占玲骅, 等, 2022. 基于高光谱遥感的上海市黑臭水体特征水质指标反演模型构建[J]. 环境污染与防治, 44(8): 1030-1034. |
殷子瑶, 李俊生, 范海生, 等, 2021. 珠海一号高光谱卫星的于桥水库水质参数反演初步研究[J]. 光谱学与光谱分析, 41(2): 494-498. |
黄华, 李茂亿, 陈吟晖, 等, 2021. 基于PLSR的珠江口城市河流水质高光谱反演[J]. 水资源保护, 37(5): 36-42. |
黄宇, 陈兴海, 刘业林, 等, 2020. 基于无人机高光谱成像技术的河湖水质参数反演[J]. 人民长江, 51(3): 205-212. |
黄李童, 陈江, 朱渭宁, 等, 2018. 基于Landsat-8的城市湖泊水体总悬浮物吸收系数的遥感反演——以杭州西湖为例[J]. 环境科学学报, 38(10): 4073-4082. |
黄昕晰, 应晗婷, 夏凯, 等, 2020. 基于无人机多光谱影像和OPT-MPP算法的水质参数反演[J]. 环境科学, 41(8): 3591-3600. |
ASKARZADEH A, 2016. A novel metaheuristic method for solving constrained engineering optimization problems: Crow search algorithm[J]. Computers & Structures, 169: 1-12. |
CAO L J, ZHANG D J, GUO Q, et al, 2021. Inversion of water quality parameter Bod5 based on hyperspectral remotely sensed data in Qinghai lake// IEEE International Geoscience and Remote Sensing Symposium IGARSS[J]. Brussels, Belgium: IEEE, 5036-5039. |
CHEN B T, MU X, CHEN P, et al, 2021. Machine learning-based inversion of water quality parameters in typical reach of the urban river by UAV multispectral data[J]. Ecological Indicators, 133: 108434. DOI:10.1016/j.ecolind.2021.108434 |
COOK K V, BEYER J E, XIAO X M, et al, 2023. Ground-based remote sensing provides alternative to satellites for monitoring cyanobacteria in small lakes[J]. Water Research, 242: 120076. DOI:10.1016/j.watres.2023.120076 |
FENG L, HU C M, CHEN X L, et al, 2014. Influence of the Three Gorges Dam on total suspended matters in the Yangtze Estuary and its adjacent coastal waters: Observations from MODIS[J]. Remote Sensing of Environment, 140: 779-788. DOI:10.1016/j.rse.2013.10.002 |
GITELSON A, GARBUZOV G, SZILAGYI F, et al, 1993. Quantitative remote sensing methods for real-time monitoring of inland waters quality[J]. International Journal of Remote Sensing, 14(7): 1269-1295. DOI:10.1080/01431169308953956 |
GUIMARÃES T T, VERONEZ M R, KOSTE E C, et al, 2019. Evaluation of regression analysis and neural networks to predict total suspended solids in water bodies from unmanned aerial vehicle images[J]. Sustainability, 11(9): 2580. DOI:10.3390/su11092580 |
LIU J, LIU J H, HE X Q, et al, 2018. Diurnal dynamics and seasonal variations of total suspended particulate matter in highly Turbid Hangzhou bay waters based on the geostationary ocean color imager[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 11(7): 2170-2180. DOI:10.1109/JSTARS.2018.2830335 |
 2024, Vol. 55
2024, Vol. 55


