
中国海洋湖沼学会主办。
文章信息
- 宗羿冰, 陈奇, 朱永兰, 唐雯雯, 蔡廷禄, 贾建军. 2024.
- ZONG Yi-Bing, CHEN Qi, ZHU Yong-Lan, TANG Wen-Wen, CAI Ting-Lu, JIA Jian-Jun. 2024.
- 筛析法分析砂砾质样品的取样质量估算——对现行国标有关规定的扩展讨论
- ESTIMATION OF SAMPLING QUALITY FOR SIEVE ANALYSIS OF SANDY AND GRAVELLY SAMPLES — DISCUSSION ON CURRENT NATIONAL STANDARDS
- 海洋与湖沼, 55(2): 386-396
- Oceanologia et Limnologia Sinica, 55(2): 386-396.
- http://dx.doi.org/10.11693/hyhz20230800173
文章历史
-
收稿日期:2023-08-24
收修改稿日期:2023-11-20
2. 自然资源部第二海洋研究所 海岸带与海岛研究中心 浙江杭州 310012
2. Second Institute of Oceanography, MNR, Hangzhou 310012, China
筛析法是沉积物粒度分析的经典方法, 其原理是按照孔径自上而下、由大到小的顺序叠置一套标准筛来分离一定量的沉积样, 通过天平称量各粒级的颗粒质量, 进而计算出该样品基于质量比的颗粒级配的频率分布或累积分布(Konert et al, 1997; 冷伟等, 2014; 罗章等, 2016; 国家能源局, 2018; 袁红旗等, 2019)。关于筛析法分析结果的表达与应用研究已经非常成熟(Kennedy et al, 1985; Blott et al, 2001; 程鹏等, 2001; 蔡廷禄等, 2014; Irham et al, 2017; 唐雯雯等, 2023), 不过, 对于砂砾质沉积物而言, 应该取用多少质量的样品进行筛析法分析仍然缺乏全面的、可操作的技术规范。现行国家标准《海洋调查规范第8部分: 海洋地质地球物理调查》(中华人民共和国国家质量监督检验检疫总局, 2008) (GB/T 12763.8—2007, 以下简称“海洋调查规范”)部分回答了这一问题, 该规范第6.3.2.1条给出最大颗粒直径[0.07 mm, 25 mm]区间内共8个最大颗粒直径及其对应的取样最小量(参见表 1), 对于海洋地质调查研究具有重要的指导价值。但是, 细究起来, 该表仍然存在三方面的不足。第一, 样品的最大颗粒直径与取样最小量之间的对应关系尚不明确, 缺乏定量的统计学解释; 第二, 数据范围较窄, 对于最大颗粒直径超过25 mm样品如何采样和取样的问题, 没有指导价值; 第三, 海洋调查规范第6.1.2.2条要求沉积物采样量不得少于1 000 g, 同时第6.3.2.1条规定采用筛析法时需要原样搅拌均匀、按四分法取样, 即粒度分析的取样质量为采样质量的1/4; 考虑到该表要求最大颗粒直径5 mm的样品之最小取样量为250 g, 那么对于最大颗粒直径5 mm以上的砂砾质样品而言, 合适的最小采样质量仍不明确(因为1 000 g的采样量显然不够用), 而对于最大颗粒直径为5 mm以下样品来说, 1 000 g的采样质量就明显冗余。
| 最大颗粒直径/mm | 取样最小量/kg |
| 25 | 10.00 |
| 19 | 5.00 |
| 13 | 2.50 |
| 9 | 1.00 |
| 6 | 0.50 |
| 5 | 0.25 |
| 3 | 0.10 |
| 0.07 | 0.01 |
本研究面向上述问题展开讨论。针对第一个问题, 本研究利用理想的正态分布模型和大量野外样品的粒度分析结果, 推导出样品的最大颗粒直径与最小取样量之间的半经验-半理论关系表达式, 解释了海洋调查规范规定的最大颗粒直径对应的取样最小量之间的对应关系——该关系可能是基于正态分布、分选极差的下界(σ=4.00 Φ)推算而来的。针对第二个和第三个问题, 本研究尝试将筛析法最小取样量的有关规定拓展到最大颗粒直径为64 mm (−6 Φ)的情形, 使得最大颗粒直径0 Φ~−6 Φ的砂砾质样品取样量都有据可循。据此, 建议海洋调查规范在后期修订时对筛析法最小取样量的规定进行解释和扩充, 以更好地发挥国家标准的指导作用。
1 材料与方法 1.1 从最粗颗粒推算粒度分布的计算方法砂的粒度范围为4 Φ~−1 Φ, 跨度为5个1 Φ间隔的粒级。为了对表 1进行适当扩充, 更好地指导砾质沉积物的筛析处理, 同样考虑从砂砾分界线上跨5个1 Φ间隔的粒级范围, 即−1 Φ~−6 Φ的砾石级颗粒。换言之, 本研究旨在探讨最粗颗粒为−6 Φ (64 mm)的砂砾质沉积物样品的取样最小量及其匹配的采样量。值得注意的是, −6 Φ作为实验室运用筛析法的上限, 已经在石油天然气行业标准《碎屑岩粒度分析方法》(国家能源局, 2018)有所体现, 该行业标准第3.2条明确要求, “(筛析法)标准套筛, 孔径0.045~64 mm……”。
1.1.1 理想化假设在自然界中, 松散沉积物大多来自不同的物源并经过多种地质营力的改造和分选, 其粒度组成常呈正态分布或者分段式地呈正态分布(Inman, 1952; 李玉文, 2001; 孙东怀等, 2001; 金秉福, 2012)。为了便于计算, 做出了以下四点假设。
Ⅰ. 假定待测松散沉积物样品的粒度分布符合正态分布。
Ⅱ. 自然界中的绝大部分松散沉积物的分选介于分选好和分选差之间(Fruth et al, 1966; Orth, 1973; Gao et al, 1994; 吴超等, 2019; 刘德政等, 2021; 参见表 2), 不失一般性, 可将沉积物的分选系数设为0.35 Φ~ 4.00 Φ。
| 分选等级 | 分选系数(σ) |
| 分选极好 | < 0.35 Φ |
| 分选好 | 0.35 Φ~0.71 Φ |
| 分选中等 | 0.71 Φ~1.00 Φ |
| 分选差 | 1.00 Φ~4.00 Φ |
| 分选极差 | > 4.00 Φ |
Ⅲ. 将松散沉积物颗粒视为理想化的等密度球体, 其密度值取作2.65 g/cm3, 由此来换算沉积物颗粒的体积与质量(付旭东等, 2004; 杨期君等, 2014)。
Ⅳ. 理论最小取样量的内涵是: 在满足概率分布规律的前提下, 尽量减少筛析法的实验室工作量, 也就是减少筛析法样品的总质量。根据一个样品各粒级的概率分布, 将其映射到筛析法分析结果, 其实是各粒级沉积物颗粒的质量比。在等密度假设条件下, 颗粒的质量与其粒径的三次方成正比; 若想得到最小取样量, 只能将各粒级的颗粒数量尽可能地降低, 尤其是粗颗粒的数量要少, 最好可以让最粗粒级的颗粒数减小到极限(个位数)。
1.1.2 基于正态分布进行推算有了上述假设, 我们可以利用正态分布2σ原则(图 1)确定研究样本的主体, 在此基础上, 将样本主体以1/2 Φ为间隔划分出多个粒级区间, 进而可以计算得出最大颗粒直径对应的理论分析取样最小量及整个样品的粒度分布。计算流程如下(图 2)。
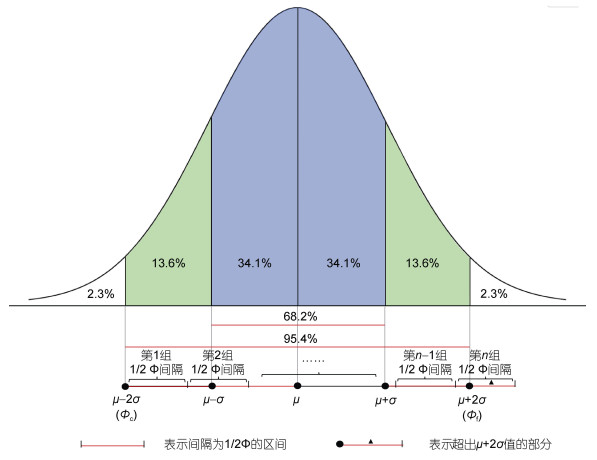 |
| 图 1 正态分布曲线与一个以1/2 Φ间隔进行模拟筛析的样品粒度的对应关系 Fig. 1 The correspondence between normal distribution curve and sample particle size obtained from simulated sieving at 1/2 Φ interval 注: μ为样本平均值, 即平均粒径; σ为标准偏差, 即分选系数; Φc与Φf分别是占样品95.4%的主体部分粗、细两端的粒度 |
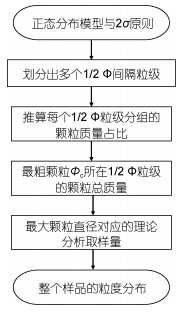 |
| 图 2 根据最粗颗粒的粒度及样品的标准偏差推算整个样品的粒度分布流程图 Fig. 2 A flow chart of the estimation of particle size distribution of sample based on its coarsest particle size and standard deviation |
A. 正态分布与2σ原则。根据正态分布规律, 一个平均粒径为μ、标准偏差为σ的正态分布样本95.4%的数值位于(μ−2σ, μ+2σ)区间。天然的沉积物样品经常混有一些异常颗粒(即与样品中大多数颗粒相比明显过大或者过小), 本研究重点考虑(μ−2σ, μ+2σ)区间内95.4%的样本主体, 这样既可以剔除近5%的异常颗粒, 又能保证分析结果的总体代表性。
用Φ值表示粒度变量, Φc与Φf分别是主体区间粗、细两端的粒度(参见图 1), 且标准偏差σ由上述假设Ⅱ与图 1已知, 则:
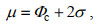 (1)
(1)即: 在(μ−2σ, μ+2σ)区间内, 平均粒径μ近似于最粗颗粒的粒径加上2σ。
B. 以1/2 Φ为间隔划分粒级。海洋调查规范要求筛析法所用标准筛的筛径间隔不得小于1/2 Φ, 故以1/2 Φ的跨度进行粒级分组来模拟筛析法的分析结果: 将最粗颗粒Φc设置为起始点, 以1/2 Φ为间隔逐级相加, 直至最细(最右侧)粒级能覆盖μ+2σ (Φf)的粒度值; 若最右侧一组1/2 Φ粒级有超出μ+2σ值的部分, 则将超出的部分剔除掉(参见图 1), 以保证参与计算的数据均为(μ−2σ, μ+2σ)区间。最终将一个样品划分为n组1/2 Φ间隔的粒级(1~n组的划分顺序为从左至右)。
C. 推算每个1/2 Φ粒级分组的颗粒质量占比。若随机变量x (在本研究中为Φ值粒度)服从正态分布, 其概率密度函数f(x)表达式如下(胡泳, 2009):
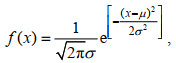 (2)
(2)进而可通过公式(3)求得每个1/2 Φ粒级分组的颗粒质量占比。
 (3)
(3)式中, Pi表示第i个1/2 Φ粒级分组的颗粒质量占比(%), Ai1与Ai2分别表示该1/2 Φ粒级最左侧与最右侧(即粗细两端)的粒度值(Φ值)。
D. 推算最粗颗粒Φc所在的1/2 Φ粒级的颗粒数与质量。由上述假设Ⅳ可知, 若想得到取样最小量, 只能将各粒级的颗粒数量尽可能地降低, 尤其是粗颗粒的数量要少。为此, 令Φc所在1/2 Φ粒级内的颗粒数W = 64/X1 (其中X1为Φc对应的毫米值), 这样可以使最粗颗粒的个数W最小化。
利用公式(4)可以求得Φc所在1/2 Φ粒级单个标准球体的质量:
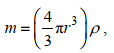 (4)
(4)式中, m为单个标准球体质量, 单位为g; r为球体的半径(等于粒度值的一半), 单位为mm; ρ为2.65 g/cm3, 即前文假设Ⅲ的理想化等密度球体的密度值。
Φc所在1/2 Φ粒级的颗粒数与单个标准球体的质量相乘即得到Φc所在的1/2 Φ粒级的颗粒总质量, 用公式(5)计算:
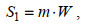 (5)
(5)式中, S1表示Φc所在1/2 Φ粒级的颗粒总质量, 单位为g。
E. 计算最大颗粒直径对应的理论分析取样最小量Q:
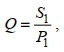 (6)
(6)式中, P1为Φc所在的1/2 Φ粒级的质量占比(%), 由步骤C可知。
F.与实际样品的分粒级数据进行比对, 通过公式(7)可计算每个1/2 Φ粒级的颗粒总质量, 从而得以分析样品整体的粒度分布情况。
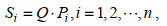 (7)
(7)式中, Si表示第i个1/2 Φ粒级的颗粒总质量, 单位为g。
1.2 对推算结果进行检验 1.2.1 数据来源为了验证上述理论分析值是否合适, 本研究收集了两批样品数据进行比对分析。第一批样品来自浙江舟山潮间带, 采样时间为2021年上半年, 涉及舟山、普陀山、桃花、朱家尖、虾峙等海岛, 共1 072个样本, 实地采样量均大于2 000 g; 这些样品包括砾石、砂、泥等组分, 其中有113个样品使用筛析法进行粒度分析, 最粗粒径不超过−6 Φ。第二批样品来自浙江省象山县, 采样时间为2022年7月份, 在风门口和毛湾村两个砾石滩共布置了46个砾石样方(0.5 m×0.5 m), 每个样方采样量在330~ 45 000 g不等; 在现场用自行研发的砾石粒度粒形分析装置, 即“砾石粒度粒形自动测量系统”(gravel grain size and shape automatic measurement system, GraSSAMS)对样方的全部沉积物颗粒进行拍照, 其取样分析量等于采样量; 后期用GraSSAMS分析每个样方的照片, 依据图像识别技术获得样方的粒度分布, 并自动计算出粒度参数。图像识别技术进行粒度分析的基本原理是: 根据体视学原理, 三维空间内特征点的特征可以用二维截面内特征点的特征来表征, 即在计算机上对二维图像进行扫描, 并对特征点的像素群进行测量统计、编辑处理、得到二维图像的特征值, 从而得出沉积物粒度分布结果(国家能源局, 2018; Zhu et al, 2023)。关于GraSSAMS的技术细节详见(Zhu et al, 2023)。样品站位如图 3所示。
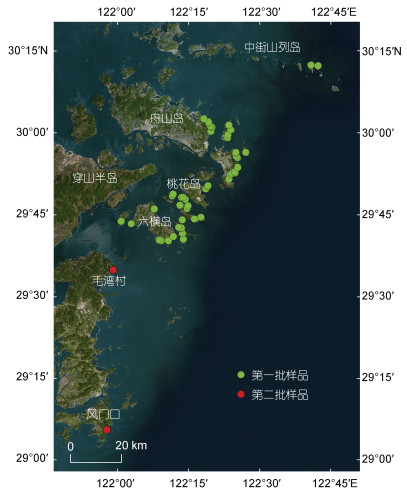 |
| 图 3 本文收集的两批样品的站位状况 Fig. 3 The locations of two sets of samples collected in this study 注: 由于图 3比例尺较小, 所以图上仅展示第一批中使用筛析法分析的样品与第二批样品所在剖面的地理位置 |
验证理论分析取样量与实际取样量的近似度, 基本思路是:
(1) 比较理论分析取样量与实际取样量两组数值的大小;
(2) 利用每个样品的最大颗粒直径、分选系数, 通过公式(1)~(7)得出每个样品的正态分布数据, 与这些样品的实测粒度分布数据构成两组数列, 运用4个评价指标对这两组数列之间的近似度进行分析, 从而判断理论分析取样量与实际取样量的相宜度。这4个评价指标分别为决定系数(R2)、皮尔逊相关系数(p)、均方根误差(RMSE)、对称平均绝对百分比误差(SMAPE)。
决定系数R2用来量化理论分析取样量(预测值)和实际取样量(真实值)之间的相关性, 计算公式为
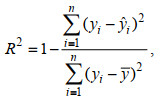 (8)
(8)式中, n表示间隔1/2 Φ的粒级个数, yi为实际取样值, 
皮尔逊相关系数是用于度量两个变量之间的相关(线性相关), 其值介于−1与1之间, 可用(9)式计算:
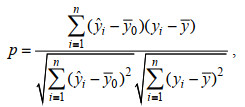 (9)
(9)式中, p为皮尔逊相关系数, y0为理论分析值均值。p范围为[−1, 1], 其中0代表无相关性, 负值代表负相关, 正值代表正相关; 0.4 < |p|≤0.6表示中等程度相关, 0.6 < |p|≤0.8表示强相关, 0.8 < |p|≤1.0表示极强相关。
均方根误差(RMSE)是预测值与真实值偏差的平方与观测次数n (即间隔1/2 Φ的粒级个数)比值的平方根, 用来衡量预测值与真实值之间的偏差, 并且对数据中的异常值较为敏感。RMSE计算公式为
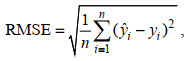 (10)
(10)式中, RMSE范围为[0, +∞)。当理论分析取样量与实际取样量完全吻合时, RMSE=0, 此时为完美模型; 误差越大, 该值越大。令
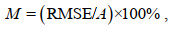 (11)
(11)式中, A表示实际取样量。一般认为, M < 15%表示误差合理。
对称平均绝对百分比误差(SMAPE)是一种度量预测值与实际值偏差程度的指标, 它衡量以百分比形式表示预测值与实际值之间的偏差程度, 计算公式为
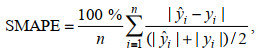 (12)
(12)SMAPE范围为[0%, 200%], 当SMAPE=0%时表示完美模型, 越大表示模型拟合度越低, 上限为200%。一般认为, SMAPE < 100%表示模型模拟程度适中。
1.2.3 验证步骤第一步, 检查各样品粒度分布直方图, 若为单峰分布则保留该样品进行后续计算; 若为多峰分布, 且当非主峰位于主峰左(右)侧、非主峰粒级的占比与其右(左)侧1/2 Φ粒级占比的差值小于5%时, 也将其视为单峰分布进行后续计算(图 4a, 4b), 否则舍弃该样品(图 4c、4d)。多峰样品的筛选实例参见图 4。
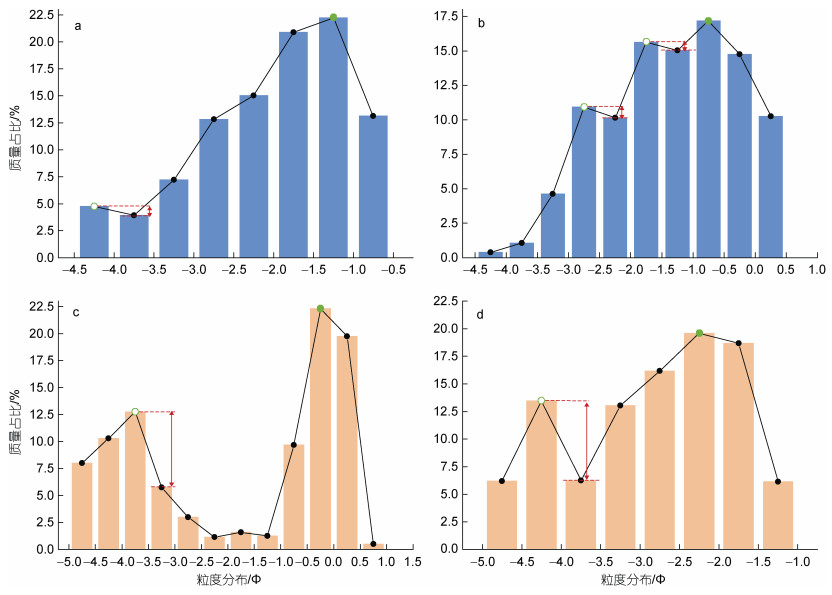 |
| 图 4 多峰样品的筛选实例图 Fig. 4 A histogram showing the selection of multi-peak samples 注: a与b表示样品粒度分布虽为多峰、可视为单峰的情况, c与d表示样品粒度分布为多峰、不能视为单峰的情况; 主峰的值用绿色实心圆表示, 非主峰的值用绿色空心圆表示, 红色箭头表示非主峰位于主峰左(右)侧时与其右(左)侧1/2 Φ粒级占比的差值。筛选原则为: 红色箭头表示的差值范围小于5%视为单峰, 参与后续的对比分析 |
第二步, 通过公式(1)~(7)可以在给定分选系数的情况下, 计算出最大颗粒直径对应的理论分析取样量以及每个1/2 Φ粒级内的理论分析取样量, 进而利用公式(8)~(12)进行理论计算值与实际数据的验证分析。
验证结果会出现4种情形: ①若理论分析取样量大于实际取样量, 且同时满足R2 > 0.5与p > 0.4, 表明理论分析取样量合理; ②若理论分析取样量大于实际取样量, 但不能同时满足R2 > 0.5与p > 0.4, 则表明实际取样时应该增加取样量、使之与理论分析取样量看齐; ③若理论分析取样量小于实际取样量, 但同时满足R2 > 0.5与p > 0.4, 表明实际取样量可能偏大; ④若理论分析取样量小于实际取样量, 且不能同时满足R2 > 0.5与p > 0.4, 则表明该样品虽然满足单峰分布, 但是可能不符合正态分布。一般情况, 将①~③视为满足或近似正态分布的情形, ④视为偏离正态分布的情形。上述4种情形都应考虑RMSE与SMAPE, 且均需满足: M < 15%, SMAPE < 100%, 不满足则视为情形④。
2 结果 2.1 理论分析值与现行海洋调查规范规定的取样最小量的对比分析根据海洋调查规范规定的最大颗粒直径与取样最小量的关系(参见表 1)拟合出一条幂函数曲线(简称为曲线1, 即图 5之蓝线), 并在分选系数为1.00 Φ、2.00 Φ、3.00 Φ、4.00 Φ的情况下拟合出最大颗粒直径与理论分析取样量4条幂函数曲线(简称为曲线2, 即图 5之红线)。通过对比两条曲线可以得出: (1) 在分选中等的情况下(σ=1.00 Φ), 曲线2的y值明显低于曲线1的y值(图 5a); (2) 随着分选系数增大、分选变差, 曲线2逐渐接近曲线1, 两曲线的y值差距逐渐缩小(图 5b, 5c); (3) 在分选极差的情况下(σ=4.00 Φ), 曲线2的最大颗粒直径为25 mm时对应的取样最小量约为7 300 g, 与海洋调查规范规定的最大颗粒直径为25 mm时对应的取样最小量为10 000 g的数值相比已经较为接近(图 5d)。
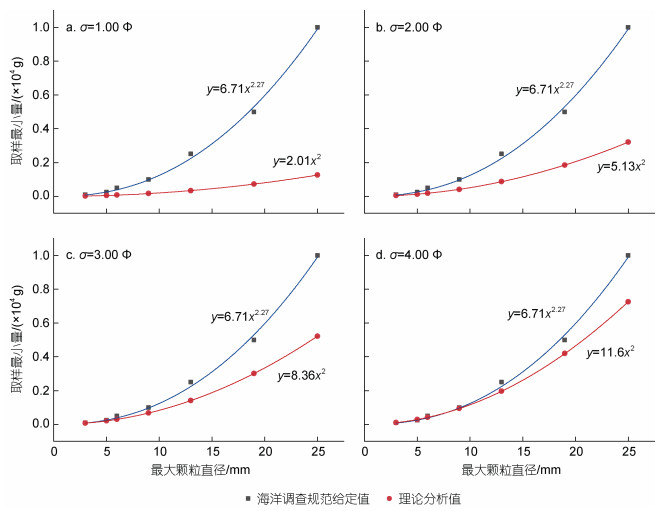 |
| 图 5 海洋调查规范与理论分析下最大颗粒直径与取样最小量关系曲线 Fig. 5 Relationships between maximum particle size and corresponding minimum quantity for grain-size analysis on the basis of two sets of rules: the specification for oceanographic survey vs statistical calculation 注: a. σ=1.00 Φ, b. σ=2.00 Φ, c. σ=3.00 Φ, d. σ=4.00 Φ |
图 6展示了将最大颗粒直径区间扩展至−6 Φ~0 Φ、且分选系数0.35 Φ~4.00 Φ的情况下, 本研究推算的取样最小量与海洋调查规范推荐值的对比, 可以发现: (1) 在不同的分选系数下, 最大颗粒直径与理论分析取样最小量在对数坐标系下均呈现为线性正相关; (2) 在同样的最大颗粒直径下, 分选系数增大, 取样最小量也增加; (3) 随着最大颗粒直径的增加, 对应的取样最小量的取值范围也逐渐扩大; (4) 当σ=4.00 Φ时, 本研究推算的理论取样最小量(图 6之深绿线)和海洋调查规范的推荐值(图 6之橙点)非常接近。因此, 依据图 5与图 6展示的统计学分析结果, 推测海洋调查规范给出取样最小量推荐值时并没有考虑分选系数不同的情况, 而是仅考虑了较差的分选系数值(σ=4.00 Φ); 这是因为, 较差的分选系数对应较大的取样最小量, 从而能够满足所有分选系数较好的样品的筛析法需求。
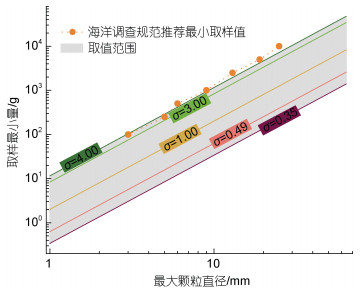 |
| 图 6 根据正态分布推算的最大颗粒直径与取样最小量的关系曲线 Fig. 6 Relationships between maximum particle size and corresponding minimum quantity for grain-size analysis based on normal distribution calculation |
第一批样品中进行筛析法分析的共113个, 主要粒径区间为−5.5 Φ~0 Φ, 分选系数范围为0.3 Φ~2.3 Φ, 实际取样量大部分介于300~600 g; 根据前述原则剔除了非单峰分布的28个样品后, 余下85个样品。第二批样品共46个, 主要粒径区间为−7 Φ~−2 Φ, 分选系数范围为0.25 Φ~0.92 Φ, 相较于第一批样品, 该批样品明显较粗, 分选较好; 根据前述原则剔除了非单峰分布的4个样品后, 保留42个样品进行后续分析。这样, 两批共有127个样品用于下列对比分析(本节下文的“全部样品”即指这127个样品)。
图 7为全部样品实际取样量与理论最小取样量近似度分析的4个评价指标的结果, 可以得出: (1) R2 > 0.5的样品共57个, 占全部样品的44.9%, 57个样品的RMSE与SMAPE值均符合1.2.3节规定的要求(M < 15%, SMAPE < 100%, 下同); (2) p > 0.4的样品共89个, 占全部样品的70.1%(其中有4个样品的RMSE与SMAPE值不符合1.2.3节规定的要求, 除去这4个异常样品后, 占全部样品的66.9%); (3) M < 15%的样品共109个, 占全部样品的85.8%; (4) SMAPE < 100%的样品共103个, 占全部样品的81.1%。
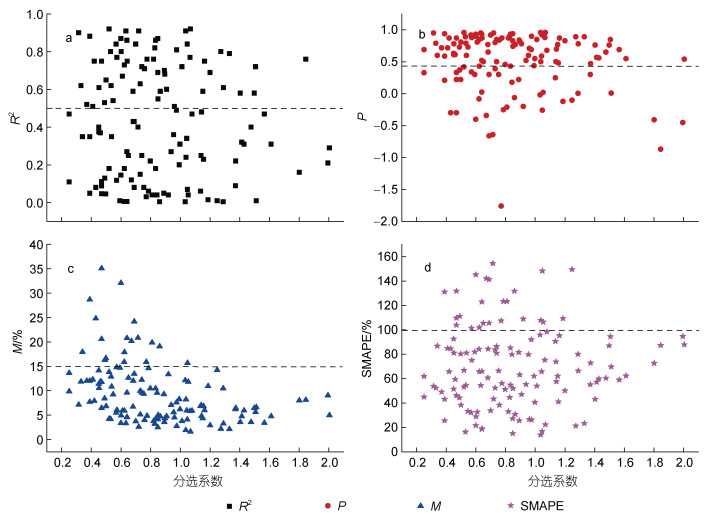 |
| 图 7 全部样品的实际取样量与理论最小取样量的4个评价指标的结果 Fig. 7 The results of the four evaluation indicators for the actual sampling quantity and the theoretical minimum sampling quantity of all samples 注: R2为决定系数; P为皮尔逊相关系数; M为(均方根误差/实际取样量)×100%; SMAPE为对称平均绝对百分比误差; 黑色虚线在a、b、c、d四图分别指R2=0.5, P=0.4, M=15%, SMAPE=100% |
根据上述结果可以发现, 单峰分布的样品中理论分析取样量与实际取样量的相关性较好, 大部分样品近似正态分布。
根据表 2的分选程度等级, 将全部样品按照分选程度分为4个区间: (0 Φ~0.35 Φ)、(0.35 Φ~0.71 Φ)、(0.71 Φ~1.00 Φ)、(1.00 Φ~4.00 Φ)。图 8为全部样品在不同分选程度下的理论分析取样量与实际取样量的对比状况, 可以看出: (1) 在样品分选系数σ < 0.35 Φ时, 所有样品的理论分析取样量均小于实际取样量; (2) 在0.35 Φ < σ < 0.71 Φ时, 约60%的样品理论分析取样量大于实际取样值; (3) 在0.71 Φ < σ < 1.00 Φ时, 绝大部分样品的理论分析取样量大于实际取样量; (4) 在1.00 Φ < σ < 4.00 Φ时, 几乎全部样品的理论分析取样量均大于实际取样量。即总体趋势为随着分选系数增大, 样品的理论分析取样量逐渐大于实际取样量, 交界点在σ=0.64 Φ附近。
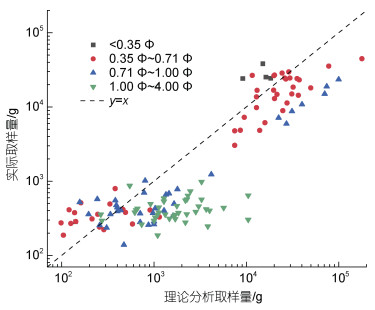 |
| 图 8 全部样品不同分选程度下理论分析取样量与实际取样量的对比 Fig. 8 Comparison of sampling quantity for theoretical analysis and actual sampling quantity for all samples at different degrees of sorting |
表 3展示了全部样品粒度分析结果的正态性检验情况, 可以看出: 不论分选系数的好坏, 样品的正态性检验结果主要集中于结果①、②与③, 占比可达到74%, 结果④占比相对较少, 有26%。这表明, 大部分样品的取样情况符合或接近正态分布。
| 分选系数区间 | 样品数量/个 | 近似正态分布的情形 | 偏离正态分布的情形 | |||||
| 结果①/个 | 结果②/个 | 结果③/个 | 占比/% | 结果④/个 | 占比/% | |||
| < 0.35 Φ | 5 | 0 | 0 | 3 | 60.0 | 2 | 40.0 | |
| 0.35 Φ~0.71 Φ | 48 | 12 | 8 | 11 | 64.6 | 17 | 35.4 | |
| 0.71 Φ~1.00 Φ | 35 | 12 | 9 | 6 | 77.1 | 8 | 22.9 | |
| 1.00 Φ~4.00 Φ | 39 | 15 | 17 | 1 | 84.6 | 6 | 15.4 | |
| 全体数据 | 127 | 39 | 34 | 21 | 74.0 | 33 | 26.0 | |
根据中心极限定理(Brosamler, 1988; 苏淳等, 1998; 杨桂元, 2000), 只要样本数量足够大, 那么估计量就越逼近于正态分布真实值。但是, 用于筛析法的取样量如果过大, 将带来人力物力的浪费, 导致实验分析效率低下, 且大量采样也会破坏样品所在的自然环境。本研究基于理想化的假设, 推算出在已知一个样品的最大颗粒直径的前提下, 其对应的取样最小量不是一个具体的值、而是一个区间, 区间内数值的驱动因素是分选系数: 分选好则取样最小量较少, 分选差则取样最小量较多(图 5)。再通过公式(1)~(7)将最大颗粒直径与取样最小量之间通过分选系数联系起来, 在明确最大颗粒直径与分选系数的前提下, 可以求得对应的取样最小量。这项工作对于砂砾级样品的筛析法工作具有一定的指导价值。
分选系数是用来评判松散碎屑沉积物的颗粒粗细的均匀程度的参数(何华春等, 2005; Su et al, 2021), 受物源、沉积环境及粒度分析方法等影响巨大(贾建军等, 2002; 张伯虎等, 2011; 杨阳等, 2016)。随着分选系数的变化, 实际取样量也会发生变化(Rana et al, 1973; Knighton, 1980)。自然界中的绝大多数松散沉积物的分选系数集中于0.35 Φ~4.00 Φ。我们统计了含有直径 < 0 Φ颗粒的样品的分选系数分布状况(表 4), 可以发现: 在706个样品中, 分选系数介于0.35 Φ~ 4.00 Φ的样品共693个, 占比98.2%; 分选系数介于0.49 Φ~3.00 Φ的样品共669个, 占比近95%; 分选系数极好与极差的样品很少, 仅占样品总量的1.8%; 此外, 分选系数 < 0.49 Φ与 > 3.00 Φ的样品数量占比接近, 均为2.5%左右。
| 分选等级 | 标准偏差 | 样品数量/个 | 占比/% |
| 分选极好 | < 0.35 Φ | 10 | 1.4 |
| 分选好 | 0.35 Φ~0.49 Φ | 8 | 1.1 |
| 0.49 Φ~0.71 Φ | 141 | 20 | |
| 分选中等 | 0.71 Φ~1.00 Φ | 152 | 21.5 |
| 分选差 | 1.00 Φ~3.00 Φ | 376 | 53.3 |
| 3.00 Φ~4.00 Φ | 16 | 2.3 | |
| 分选极差 | > 4.00 Φ | 3 | 0.4 |
本研究主要考虑分选系数介于0.35 Φ~4.00 Φ的松散沉积物。同时, 统计显示, 收集的样品中近95%的分选系数介于0.49 Φ~3.00 Φ。若将分选系数取值范围从0.35 Φ~4.00 Φ进一步缩小至0.49 Φ~3.00 Φ, 既可以保证整体数据的代表性与准确性, 又能够达到较大幅度缩小取样量的目的(分选系数介于0.35 Φ~ 4.0 Φ与0.49 Φ~3.00 Φ两个范围内的最大颗粒直径对应的理论分析取样最小量对比参见图 6)。由此建议, 在海洋调查规范修订时, 可以将分选系数缩小至0.49 Φ~3.00 Φ区间以推算最小取样量的范围。
3.2 对海洋调查规范有关规定的修改建议经过前文的分析和计算, 我们对现行海洋调查规范的有关规定提出如下修改建议:
(1) 筛析法取样量的要求: 样品的取样量可以按照公式(1)~(7)进行计算, 扩展后的筛析法粒度分析取样质量估算值列于表 5; 其中, 理论分析取样量下限为分选系数σ=0.35 Φ时, 最大颗粒直径对应的理论分析取样量; 理论分析取样量上限为分选系数σ=4.00 Φ时, 最大颗粒直径对应的理论分析取样量。同时, 建议海洋调查规范在“筛析法粒度分析取样质量估算表”增加以下说明文字: 表中数据是基于正态分布、分选极差的下界σ=4.00 Φ的情况推算而来。
| 最大颗粒直径/Φ | 理论分析取样量下限/g(σ=0.35 Φ) | 理论分析取样量上限/g(σ=4.00 Φ) |
| −6.0 | 1392.4 | 47835.5 |
| −5.5 | 696.5 | 23917.8 |
| −5.0 | 348.1 | 11958.0 |
| −4.5 | 173.6 | 5979.4 |
| −4.0 | 87.0 | 2989.7 |
| −3.5 | 43.4 | 1494.9 |
| −3.0 | 21.8 | 747.4 |
| −2.5 | 11.0 | 373.7 |
| −2.0 | 5.4 | 186.9 |
| −1.5 | 2.7 | 93.4 |
| −1.0 | 1.4 | 46.7 |
| −0.5 | 0.7 | 23.3 |
| 0.0 | 0.3 | 11.7 |
(2) 采样量的要求: 砂砾质沉积物的采样量需要根据最大颗粒直径对应的取样最小量乘以四倍为基准采样, 采样量需大于或等于此基准, 且最少不得少于1 000 g。
(3) 通过查询图 6与表 5可以使得读者清晰地得出最大颗粒直径对应的理论分析取样最小量的范围区间, 故建议海洋调查规范将本文的图 6与表 5收录为资料性附录。
4 结论针对砂砾质沉积物进行筛析法粒度分析时的采样量与取样量的定量关系问题, 本研究基于正态分布的数学原理, 从样品最粗颗粒直径推算出整个样品的筛析法最小取样量及其理想粒度分布的计算公式。利用该计算公式得出的结果与实际样品的分析结果进行对比发现, 在单峰分布的样品中, 本研究推算的理论最小取样量与实际样品取样量的相关性较为理想, 具有指导意义和推广价值。同时, 研究表明, 运用筛析法进行粒度分析时, 现行海洋调查规范给出的最大颗粒直径对应的取样最小量可能是基于正态分布、分选极差的下界(σ=4.00 Φ)的情况推算得出的。
建议海洋调查规范补充说明“筛析法粒度分析取样质量估算表”的计算依据, 并将有关要求进行合理的扩展: 当砂砾质样品最大颗粒直径为−6 Φ时, 筛析法需要的最小取样量约50 kg; 同时建议海洋调查规范将本文的图 6与表 5收录为资料性附录。
中华人民共和国国家质量监督检验检疫总局, 2008. 海洋调查规范 第8部分: 海洋地质地球物理调查: GB/T 12763.8-2007[S]. 北京: 中国标准出版社.
|
付旭东, 杨小平, 2004. 中国北方沙漠石英δ18O值的初步测定与分析[J]. 第四纪研究, 24(2): 243. |
刘德政, 夏非, 2021. 江苏中部海岸晚第四纪沉积物的粒度与磁化率特征及其古环境意义[J]. 海洋地质与第四纪地质, 41(5): 210-220. |
孙东怀, 安芷生, 苏瑞侠, 等, 2001. 古环境中沉积物粒度组分分离的数学方法及其应用[J]. 自然科学进展, 11(3): 269-276. |
苏淳, 迟翔, 1998. 非平稳NA序列中心极限定理的一些结果[J]. 应用数学学报, 21(1): 9-21. |
李玉文, 1991. 关于峰态的一个新公式[J]. 沉积与特提斯地质, 12(2): 36-39. |
杨阳, 高抒, 周亮, 等, 2016. 海南新村港潟湖表层沉积物粒度特征及其沉积环境[J]. 海洋学报, 38(1): 94-105. |
杨桂元, 2000. 中心极限定理及其在统计分析中的应用[J]. 统计与信息论坛, 15(3): 13-15. |
杨期君, 赵春风, 2014. 水合物沉积物力学性质的三维离散元分析[J]. 岩土力学, 35(1): 255-262. |
吴超, 郑祥民, 王辉, 等, 2019. 长江三角洲第一硬质黏土层粒度多元统计分析及沉积环境判别[J]. 沉积学报, 37(1): 115-123. |
何华春, 丁海燕, 张振克, 等, 2005. 淮河中下游洪泽湖湖泊沉积物粒度特征及其沉积环境意义[J]. 地理科学, 25(5): 590-596. |
冷伟, 范代读, 2014. 联用筛析法与激光法进行粒度接序分析的界点选择[J]. 沉积学报, 32(3): 478-484. |
国家能源局, 2018. 碎屑岩粒度分析方法: SY/T 5434-2018[S]. 北京: 石油工业出版社.
|
罗章, 蔡斌, 陈沈良, 2016. 动态图像法应用于海滩沉积物粒度粒形测试及其与筛析法的比较[J]. 沉积学报, 34(5): 881-891. |
张伯虎, 陈沈良, 刘焱雄, 等, 2011. 广西钦州湾海域表层沉积物分异特征与规律[J]. 热带海洋学报, 30(4): 66-70. |
金秉福, 2012. 粒度分析中偏度系数的影响因素及其意义[J]. 海洋科学, 36(2): 129-135. |
胡泳, 2009. 正态分布[J]. 商务周刊, (24): 94. |
袁红旗, 王蕾, 于英华, 等, 2019. 沉积学粒度分析方法综述[J]. 吉林大学学报(地球科学版), 49(2): 380-393. |
贾建军, 高抒, 薛允传, 2002. 图解法与矩法沉积物粒度参数的对比[J]. 海洋与湖沼, 33(6): 577-582. |
程鹏, 高抒, 李徐生, 2001. 激光粒度仪测试结果及其与沉降法、筛析法的比较[J]. 沉积学报, 19(3): 449-455. |
唐雯雯, 陈奇, 朱永兰, 等, 2023. 激光-筛分联合法粒度分析结果的表达及粒度端元的沉积动力学意义[J]. 海洋通报, 42(4): 361-374. |
蔡廷禄, 贾建军, 汪亚平, 2014. 河口海岸和近海沉积物的粒度资料同化技术[J]. 海洋地质与第四纪地质, 34(1): 185-193. |
BLOTT S J, PYE K, 2001. GRADISTAT: a grain size distribution and statistics package for the analysis of unconsolidated sediments[J]. Earth Surface Processes and Landforms, 26(11): 1237-1248. DOI:10.1002/esp.261 |
BROSAMLER G A, 1988. An almost everywhere central limit theorem[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 104(3): 561-574. DOI:10.1017/S0305004100065750 |
FOLK R L, WARD W C, 1957. Brazos River bar: a study in the significance of grain size parameters[J]. Journal of Sedimentary Research, 27(1): 3-26. DOI:10.1306/74D70646-2B21-11D7-8648000102C1865D |
FRUTH L S, ORME G R, DONATH F A, 1966. Experimental compaction effects in carbonate sediments[J]. Journal of Sedimentary Research, 36(3): 747-754. |
GAO S, COLLINS M B, 1994. Analysis of grain size trends, for defining sediment transport pathways in marine environments[J]. Journal of Coastal Research, 10(1): 70-78. |
INMAN D L, 1952. Measures for describing the size distribution of sediments[J]. Journal of Sedimentary Research, 22(3): 125-145. |
IRHAM M, FIBRIARISTA I, SUGIANTO S, et al, 2017. The spatial distribution of bed sediments at Krueng cut estuary: the sieve analysis approach[J]. Jurnal Rekayasa Kimia & Lingkungan, 12(2): 69-76. |
KENNEDY S K, MELOY T P, DURNEY T E, 1985. Sieve data-size and shape information[J]. Journal of Sedimentary Research, 55(3): 356-360. |
KNIGHTON A D, 1980. Longitudinal changes in size and sorting of stream-bed material in four English rivers[J]. GSA Bulletin, 91(1): 55-62. DOI:10.1130/0016-7606(1980)91<55:LCISAS>2.0.CO;2 |
KONERT M, VANDENBERGHE J E F, 1997. Comparison of laser grain size analysis with pipette and sieve analysis: a solution for the underestimation of the clay fraction[J]. Sedimentology, 44(3): 523-535. DOI:10.1046/j.1365-3091.1997.d01-38.x |
ORTH R J, 1973. Benthic infauna of eelgrass, Zostera marina, beds[J]. Chesapeake Science, 14(4): 258-269. DOI:10.2307/1350754 |
RANA S A, SIMONS D B, MAHMOOD K, 1973. Analysis of sediment sorting in alluvial channels[J]. Journal of the Hydraulics Division, 99(11): 1967-1980. DOI:10.1061/JYCEAJ.0003786 |
SU M, LUO K W, FANG Y X, et al, 2021. Grain-size characteristics of fine-grained sediments and association with gas hydrate saturation in Shenhu area, northern South China Sea[J]. Ore Geology Reviews, 129: 103889. DOI:10.1016/j.oregeorev.2020.103889 |
ZHU Y L, CHEN Q, ZHANG Y, et al, 2023. GraSSAMS: A new instrument designed for the determination of grain size and shape of sand-gravel-sized sediment[J]. Estuarine, Coastal and Shelf Science, 290: 108392. DOI:10.1016/j.ecss.2023.108392 |
 2024, Vol. 55
2024, Vol. 55


