文章信息
- 李小岗, 王红都, 黎明, 刘鑫. 2020.
- LI Xiao-gang, WANG Hong-du, LI Ming, LIU Xin. 2020.
- 水下机器人-机械臂系统的滑模自抗扰控制
- Sliding mode active disturbance rejection control of underwater vehicle-manipulator system
- 海洋科学, 44(9): 130-138
- Marine Sciences, 44(9): 130-138.
- http://dx.doi.org/10.11759/hykx20190821002
-
文章历史
- 收稿日期:2019-08-21
- 修回日期:2020-02-20
2. 四川警学院 侦查系, 四川 泸州 646000
2. Sichuan Police College, Department of Investigation, Luzhou, Sichuan 646000, China
水下机器-机械臂系统(Underwater Vehicle-Manipulator System, UVMS)模型具有高度非线性、强耦合、水动力学参数变化等特点, 且其在作业过程受到复杂海洋多源干扰的作用, 这些都会严重影响UVMS的操作和定位精度等指标[1]。因此, 有必要设计具有干扰抑制与补偿能力的复合控制器, 以达到预期的抗扰等性能指标要求。
目前, UVMS已经有了较为成熟的建模与控制方法[2-4]。Fossen[2]采用牛顿-欧拉公式建立了UVMS的模型, Tarn[3]提出了一种新的基于欧拉-朗格朗日方程和牛顿-欧拉公式的模型建立公式。这两种经典的建模方法为基于模型的控制奠定了基础。Mahesh[4]研究了UVMS的协调控制, 将水下机器人和机械臂系统的相互影响进行了系统性的阐述。随着对控制精度要求的提高, 需要开发更加高效、精确的控制系统, 在此基础上许多学者提出了众多新的控制方法[5]。Huang[6]结合干扰观测器, 提出了基于模型的自适应控制; 针对UVMS的动态不确定性和时变外部扰动, Dai[7]将扩张卡尔曼滤波器引入补偿系统, 将基于模型的力矩控制器与H∞鲁棒补偿跟踪控制器结合设计了间接自适应控制器; Londhe[8]将单输入模糊控制器应用于UVMS的轨迹跟踪问题; Wang[9]采用离散延迟估计来处理未知的水动力干扰, 并针对UVMS的闭环系统进行了分析。Huang[10]将运动学和动力学控制器相结合, 设计了基于动态模型的动力学控制器相结合, 设计了基于动态模型的自适应控制器, 提高了UVMS操纵轨迹的精确性。这些方法都能达到较好的控制效果, 但是需要模型精确已知或者模型过于复杂。
韩京清[11]借鉴PID控制不依赖于模型的优点, 提出了自抗扰控制技术(Active Disturbance Rejection Control, ADRC)。其核心思想是将系统的内部不确定性与外部扰动集总为“广义总扰动”, 引入了非线性扩张状态观测器(Extended State Observer, ESO)对其进行估计; 并且在外部信号输入端加入跟踪微分器(Tracker Differential, TD)对输入信号安排过渡过程, 使得自抗扰控制具有快速的响应过程和良好的抗干扰能力[12-14]。但是其参数难以整定, 且非线性函数难以工业化的难点在很大程度上限制其工业应用。为了解决以上难点, Gao等[15]用基于带宽的思想提出了线性自抗扰控制器, 采用PD控制器替换原来的非线性误差反馈, 并将PD控制器和线性扩张状态观测器(Linear Extended State Observer, LESO)的参数与其带宽联系起来, 提出了结构相对精简的线性自抗扰控制器(Linear Active Disturbance Rejection Controller, LADRC), 该控制器极大减少了需要调节的参数。因此, LADRC技术为具有多输入多输出的AUVMS高精度控制设计带来了可能。
本文针对UVMS, 将复杂系统模型转变为简单的积分串联系统, 利用LESO可对包括建模误差、耦合、内外部干扰、海洋多源干扰在内的集总干扰进行估计并补偿, 引入滑模控制器(Sliding Mode Control, SMC)增加系统的鲁棒性, 建立了滑模自抗扰控制器(Sliding Mode Active Disturbance Rejection Control, SM-ADRC), 考虑用简单的控制结构解决UVMS的复杂控制问题, 最后仿真结果证明了该方法的有效性。首先建立了UVMS的动力学模型, 将UVMS分成6+n个子系统, 针对每一个子系统, 将内部不确定性、外部干扰和其他子系统的耦合影响集总为总扰动, 设计LESO进行估计, 再利用估计误差建立滑模面, 给出UVMS的SM-ADRC设计方法, 并进行Lyapunov稳定性分析。在此基础上得到UVMS的SM-ADRC设计方法, 并给出仿真结果, 与传统LADRC与SMC的控制结果进行对比分析。
1 UVMS动力学分析 1.1 UVMS的动力学模型作者将整个UVMS系统视为刚体, 根据Fossen[2]的建模方法建立如下UVMS动力学模型:
| $ \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} + \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) + \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) = {\mathit{\boldsymbol{\tau }}_{\rm{c}}} + {\mathit{\boldsymbol{\tau }}_{\rm{d}}} $ | (1) |
式中向量q=[X, Y, Z, ϕ, θ, Ψ, θ1, θ2, …, θn]T由船体的位置[X, Y, Z]T, 航向角[ϕ, θ, Ψ]T, 机械臂关节角度向量[θ1, θ2, …, θn]T(n为机械臂关节个数, 本文选取n=3), 因此系统总自由度为水下机器人本体的6个自由度和机械臂关节的自由度之和, 即6+n。斜对称正定矩阵M(q)是包括附加质量的系统质量矩阵, 为,
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}}) = {\mathit{\boldsymbol{M}}^{\rm{T}}}(\mathit{\boldsymbol{q}}), \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}}) > 0, \forall \mathit{\boldsymbol{q}} \in {\mathit{\boldsymbol{R}}^{6 + n}}\\ {\mathit{\boldsymbol{s}}^{\rm{T}}}{\rm{[}}\mathit{\boldsymbol{\dot M}}(\mathit{\boldsymbol{q}}) - 2\mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}})]\mathit{\boldsymbol{s}} = 0, \forall \mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{R}}^{6 + n}}, \forall \mathit{\boldsymbol{q}} \in {\mathit{\boldsymbol{R}}^{6 + n}}\\ \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) > 0, \forall \mathit{\boldsymbol{q}} \in {\mathit{\boldsymbol{R}}^{6 + n}} \end{array} \right. $ | (2) |
定义
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat M}}(\mathit{\boldsymbol{q}}) = \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}}) + \Delta \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}})\\ \mathit{\boldsymbol{\hat C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) = \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) + \Delta \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) \end{array} \right. $ | (3) |
则系统(1)可改写为:
| $ \mathit{\boldsymbol{\hat M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} + \mathit{\boldsymbol{\hat C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} = {\mathit{\boldsymbol{\tau }}_{\rm{c}}} + \mathit{\boldsymbol{f}} $ | (4) |
式中f为建模误差, 参数不确定性, 水动力阻尼影响和未知干扰等的总和, 即:
| $ \begin{array}{l} \mathit{\boldsymbol{f}} = {\mathit{\boldsymbol{\tau }}_{\rm{d}}} - \Delta \mathit{\boldsymbol{M}}(\mathit{\boldsymbol{q}})\mathit{\boldsymbol{\ddot q}} - \Delta \mathit{\boldsymbol{C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} - \\ \;\;\mathit{\boldsymbol{D}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}})\mathit{\boldsymbol{\dot q}} - \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) - \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{q}}) \end{array} $ | (5) |
且,
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\hat M}}(\mathit{\boldsymbol{q}}) = {{\mathit{\boldsymbol{\hat M}}}^{\rm{T}}}(\mathit{\boldsymbol{q}}), \mathit{\boldsymbol{\hat M}}(\mathit{\boldsymbol{q}}) > 0, \forall \mathit{\boldsymbol{q}} \in {\mathit{\boldsymbol{R}}^{6 + n}}\\ {\mathit{\boldsymbol{s}}^{\rm{T}}}[\mathit{\boldsymbol{\dot {\hat M}}}(\mathit{\boldsymbol{q}}) - 2\mathit{\boldsymbol{\hat C}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}})]\mathit{\boldsymbol{s}} = 0, \forall \mathit{\boldsymbol{s}} \in {\mathit{\boldsymbol{R}}^{6 + n}}, \forall \mathit{\boldsymbol{q}} \in {\mathit{\boldsymbol{R}}^{6 + n}} \end{array} \right. $ | (6) |
定义系统维数为m = 6+n, 因此系统模型(4)可展开为:
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1m}}}\\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{2m}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{a_{m1}}}&{{a_{m2}}}& \cdots &{{a_{mm}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\ddot y}_{_1}}}\\ {{{\ddot y}_{_2}}}\\ \vdots \\ {{{\ddot y}_m}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}& \cdots &{{c_{1m}}}\\ {{c_{21}}}&{{c_{22}}}& \cdots &{{c_{2m}}}\\ \vdots & \vdots & \ddots & \vdots \\ {{c_{m1}}}&{{c_{m2}}}& \cdots &{{c_{mm}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot y}_1}}\\ {{{\dot y}_2}}\\ \vdots \\ {{{\dot y}_m}} \end{array}} \right]\\ = \left[ {\begin{array}{*{20}{c}} {{u_1}}\\ {{u_2}}\\ \vdots \\ {{u_m}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ \vdots \\ {{f_m}} \end{array}} \right] \end{array} $ | (7) |
其中系数矩阵
图 1给出UVMS的动态模型示意图, 定义图中坐标轴Ie(X, Y, Z)为惯性坐标系, Ib(xb, yb, zb)为机身坐标系, Ii(xi, yi, zi), i=1, 2, …, n为机械臂关节自身坐标系, 其中n为机械臂关节个数, 本文只考虑机械臂关节绕Z轴旋转。
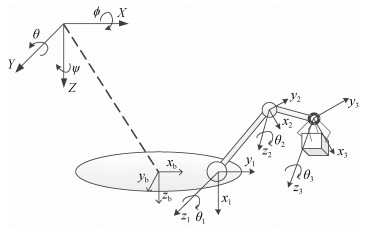 |
| 图 1 UVMS的动态模型示意图 Fig. 1 Schematic of the dynamic model of UVMS |
假设UVMS的构成为圆柱体, 则其在水下所受的黏性曳力动力学模型为[20]:
| $ {F_{{\rm{drag}}}} = \frac{1}{2}\rho {C_{\rm{d}}}(Rn)A(\alpha ){v_{\rm{r}}}\left| {{v_{\rm{r}}}} \right| $ | (8) |
式中vr为被控对象与洋流的相对速度, ρ为水密度(海水密度为1.02~1.07), Ds为线性表面摩擦系数, Dsvr即为线性表面摩擦力。A(α)为被示性曲面前部的投影横截面积, α为冲角。o(v3r)为阶数大于等于三阶的高阶相, 通常可忽略。Cd(Rn, α)为曳引系数, 由雷诺数Rn决定。而雷诺系数可以由以下公式求得:
| $ Rn = \frac{{\rho \left| {{v_{\rm{c}}}} \right|d}}{\mu } $ | (9) |
式中d是垂直于流体速度vb方向的物体的特征长度, μ为流体黏性系数。
升力垂直于流动方向。对于水下运动物体, 它们可以被建模为[20]:
| $ {F_{{\rm{lift}}}} = \frac{1}{2}\rho v_{\rm{r}}^{\rm{2}}A(\alpha ){C_{\rm{l}}}(Rn, \alpha ) $ | (10) |
式中Cl为升力系数, 由雷诺系数与冲角决定。表 1给出了圆柱体雷诺数函数的升力系数与曳力系数。
| 雷诺数 | 流态 | Cd | Cl |
| Rn < 2·105 | 亚临界流 | 1 | [3, 0.6] |
| 2·105 < Rn < 5·105 | 临界流 | [1, 0.4] | 0.6 |
| 5·105 < Rn < 3·106 | 跨临界流 | 0.4 | 0.6 |
当刚体在重力作用下浸入流体中时, 必须考虑两个主要的力:重力和浮力。后者是唯一的流体静力学效应, 它不是机身和液体之间相对运动的函数。
定义如下向量:
| $ {\mathit{\boldsymbol{g}}^{\rm{l}}} = \left[ {\begin{array}{*{20}{c}} 0\\ 0\\ {9.81} \end{array}} \right]m/{s^2} $ | (11) |
为重力加速度向量, V为机身的体积, m为质量。则物体浮重为
| $ {\mathit{\boldsymbol{f}}_{\rm{G}}}{\rm{(}}{\mathit{\boldsymbol{R}}_{\rm{t}}}) = - \mathit{\boldsymbol{R}}_{\rm{t}}^{\rm{T}}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ W \end{array}} \right] $ | (12) |
式中Rt为转移矩阵, 作用于浮心
| $ {\mathit{\boldsymbol{f}}_{\rm{B}}}{\rm{(}}{\mathit{\boldsymbol{R}}_{\rm{t}}}{\rm{)}} = - \mathit{\boldsymbol{R}}_{\rm{t}}^{\rm{T}}\left[ {\begin{array}{*{20}{c}} 0\\ 0\\ B \end{array}} \right] $ | (13) |
因此在机身坐标系内的重力和浮力作用下的力/力矩矢量可表示为:
| $ {\mathit{\boldsymbol{g}}_{{\rm{RB}}}}({\mathit{\boldsymbol{R}}_{\rm{t}}}{\rm{)}} = - \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{f}}_{\rm{G}}}({\mathit{\boldsymbol{R}}_{\rm{t}}}) + {\mathit{\boldsymbol{f}}_{\rm{B}}}({\mathit{\boldsymbol{R}}_{\rm{t}}})}\\ {\mathit{\boldsymbol{r}}_{\rm{C}}^{\rm{B}} \times {\mathit{\boldsymbol{f}}_{\rm{G}}}({\mathit{\boldsymbol{R}}_{\rm{t}}}) + \mathit{\boldsymbol{r}}_{\rm{B}}^{\rm{B}}{\mathit{\boldsymbol{f}}_{\rm{B}}}({\mathit{\boldsymbol{R}}_{\rm{t}}})} \end{array}} \right] $ | (14) |
由于假设重力作用在刚体上是一致的, 所以质心和重心是重合的。
用欧拉角可以将gRB表示为:
| $ {\mathit{\boldsymbol{g}}_{{\rm{RB}}}}(\mathit{\boldsymbol{q}})\left[ {\begin{array}{*{20}{c}} {(W - B)s\theta }\\ { - (W - B)c\theta s\phi }\\ { - (W - B)c\theta c\phi }\\ { - ({y_{\rm{G}}}W - {y_{\rm{B}}}B)c\theta c\phi + ({z_{\rm{G}}}W - {z_{\rm{B}}}B)c\theta s\phi }\\ {({z_{\rm{G}}}W - {z_{\rm{B}}}B)s\theta + ({x_{\rm{G}}}W - {x_{\rm{B}}}B)c\theta c\phi }\\ { - ({x_{\rm{G}}}W - {x_{\rm{B}}}B)c\theta s\phi - ({y_{\rm{G}}}W - {y_{\rm{B}}}B)s\theta } \end{array}} \right] $ | (15) |
式中s(.)和c(.)表示正弦与余弦函数。
当一个刚体在流体中运动时, 必须考虑围绕着它的流体的附加惯性, 也就是由于流体的运动而加速的惯性。这种效应在工业机器人中可以忽略, 因为空气的密度比移动机械系统的密度轻得多。然而在水下时水下机器人的密度相比, 水的密度ρ≈1 000 kg/m3。在0度时净水密度为1 002.68 kg/m3; 含盐量为3.5%的海水密度为1 028.48 kg/m3。
当物体具有一定速度地通过流体时, 在物体的支撑下, 周围的流体也会加速。因此, 会产生方向相反的力施加在物体上, 即附加质量力, 它可以由为一个6×6的矩阵表示。由于附加质量是物体表面几何形状的函数, 所以对于刚体的6×6惯性矩阵, 其性质各不相同。例如惯性矩阵不一定是正定的。
以沿xb方向的线性加速度所产生的水动力为例, 定义:
| $ {X_{\rm{A}}} = - {X_{\dot u}}\dot u $ | (16) |
式中:
| $ {X_{\dot u}} = \frac{{\partial X}}{{\partial \dot u}} $ | (17) |
同样地, 可定义所有与6个力/力矩分量[X, Y, Z, K, M, N]T和6个线性/角加速度相关的其余元素, 这些元素可以被分组到附加的质量矩阵MA中。对于完全浸入水中的物体则有MA > 0, 并且对于理想液体(无杂物), 物体移速较慢且无海浪或洋流时有[21]:
| $ {\mathit{\boldsymbol{M}}_{\rm{A}}} = \mathit{\boldsymbol{M}}_{\rm{A}}^{\rm{T}} > 0 $ | (18) |
附加质量也增加了科氏力和向心力, 可以用矩阵表示为:
| $ {\mathit{\boldsymbol{C}}_{\rm{A}}}{\rm{(}}\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) = - \mathit{\boldsymbol{C}}_{\rm{A}}^{\rm{T}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}), \forall q \in {\mathit{\boldsymbol{R}}^6} $ | (19) |
物体完全浸入水中, 运动速度较低, 且具有水下航行器常见的3个对称面, 则可以考虑以下矩阵MA和CA的结构:
| $ {\mathit{\boldsymbol{M}}_{\rm{A}}} = - {\rm{diag}}\left\{ {{X_{\dot u}}, {Y_{\dot v}}, {Z_{\dot w}}, {K_{\dot p}}, {M_{\dot q}}, {N_{\dot r}}} \right\} $ | (20) |
| $ {\mathit{\boldsymbol{C}}_{\rm{A}}} = \left[ {\begin{array}{*{20}{c}} 0&0&0&0&{ - {Z_{\dot w}}w}&{{Y_{\dot v}}v}\\ 0&0&0&{{Z_{\dot w}}w}&0&{ - {X_{\dot u}}u}\\ 0&0&0&{ - {Y_{\dot v}}v}&{{X_{\dot u}}u}&0\\ 0&{ - {Z_{\dot w}}w}&{{Y_{\dot v}}v}&0&{ - {N_{\dot r}}r}&{{M_{\dot q}}q}\\ {{Z_{\dot w}}w}&0&{{X_{\dot u}}u}&{{N_{\dot r}}r}&0&{ - {K_{\dot p}}}\\ { - {Y_{\dot v}}v}&{{X_{\dot u}}u}&0&{ - {M_{\dot q}}q}&{{K_{\dot p}}p}&0 \end{array}} \right] $ | (21) |
其中[u, v, w]与[p, q, r]分别对应船体的位置[X, Y, Z]与航向角[ϕ, θ, Ψ]方向上的速度。
对于质量为m, 长度为L, 截面半径为r的圆柱形刚体, 其附加质量系数可选取为:
| $ \left\{ \begin{array}{l} {X_{\dot u}} = - 0.1m\\ {Y_{\dot v}} = - {\rm{ \mathit{ π} }}\rho {r^2}L\\ {Z_{\dot w}} = - {\rm{ \mathit{ π} }}\rho {r^2}L\\ {K_{\dot p}} = 0\\ {M_{\dot q}} = - \frac{1}{{12}}{\rm{ \mathit{ π} }}\rho {r^2}{L^3}\\ {N_{\dot r}} = - \frac{1}{{12}}{\rm{ \mathit{ π} }}\rho {r^2}L \end{array} \right. $ | (22) |
在[20]中可以找到关于圆柱在流体中运动的附加质量效应的详细的理论和实验讨论, 它表明附加质量矩阵是状态相关的, 它的系数是圆柱运动距离的函数。
流体的黏度也会对物体产生耗散阻力和升力, 即为式(1)中的
| $ \mathit{\boldsymbol{D}}\left( {\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}} \right) > 0, \forall \mathit{\boldsymbol{q}} \in \mathit{\boldsymbol{R}} $ | (23) |
这个矩阵的系数也被认为是常数。对于完全浸入水中的物体, 可以做以下进一步的假设
| $ \begin{array}{l} \mathit{\boldsymbol{D}}(\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{\dot q}}) = - {\rm{diag}}\left\{ {{X_{\dot u}}, {Y_{\dot v}}, {Z_{\dot w}}, {K_{\dot p}}, {M_{\dot q}}, {N_{\dot r}}} \right\} - \\ \;\;\;\;\;\;{\rm{diag}}\left\{ {{X_{u\left| u \right|}}\left| u \right|, {Y_{v\left| v \right|}}\left| v \right|, {Z_{w\left| w \right|}}\left| w \right|, {K_{p\left| p \right|}}\left| p \right|, {M_{q\left| q \right|}}\left| q \right|, {N_{r\left| r \right|}}\left| r \right|} \right\} \end{array} $ | (24) |
需要注意的是当假定阻尼矩阵为对角结构时就意味着忽略耦合耗散项。
2 滑模自抗扰控制器系统(7)是一个高维不确定系统。为了方便进行控制设计, 根据其具体维数将UVMS分成m个子系统, 针对每一个子系统, 将建模误差, 外部干扰和其他子系统的耦合影响等集总为总扰动, 设计LESO进行估计, 再利用估计误差建立滑模面, 构造滑模控制器。在此基础上得到针对整个UVMS的SM-ADRC设计方法。
2.1 线性扩张观测器以系统(7)中的第一个子系统为例:
| $ {a_{11}}{{\ddot y}_1} + \cdots + {a_{1m}}{{\ddot y}_m} + {c_{11}}{{\dot y}_1} + \cdots + {c_{1m}}{{\dot y}_m} = {u_1} + {f_1} $ | (25) |
再对其进行移项可得:
| $ \begin{array}{l} {{\ddot y}_1} = - \frac{{{a_{12}}{{\ddot y}_2} + \cdots + {a_{1m}}{{\ddot y}_m} + {c_{11}}{{\dot y}_1} + \cdots + {c_{1m}}{{\dot y}_m} + {f_1}}}{{{a_{11}}}}\\ \;\; + \frac{1}{{{a_{11}}}}{u_1} \end{array} $ | (26) |
定义
| $ \left\{ \begin{array}{l} {\xi _1} = \frac{{{a_{12}}{{\ddot y}_2} + \cdots + {a_{1m}}{{\ddot y}_m} + {c_{11}}{{\dot y}_1} + \cdots + {c_{1m}}{{\dot y}_m} + {f_1}}}{{{a_{11}}}}\\ {b_1} = \frac{1}{{{a_{11}}}} \end{array} \right. $ | (27) |
式中为ξ1子系统(25)的广义总扰动, 包含了内部的不确定性和外部未知干扰, 假设其未知但有界。则系统(26)可重新写作:
| $ {{\ddot y}_1} = {b_1}{u_1} + {\xi _1} $ | (28) |
现将总扰动ξ1扩展为系统的状态变量x3=ξ1, 同时假设其微分有界, 并定义
| $ \left\{ \begin{array}{l} {y_1} = {x_1}\\ {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = {x_3} + {b_1}{u_1}\\ {{\dot x}_3} = w \end{array} \right. $ | (29) |
其矩阵形式为:
| $ \left\{ \begin{array}{l} \dot x = Ax + Bu + Ef\\ y = Cx \end{array} \right. $ | (30) |
基于状态方程(29)可以建立如下观测器:
| $ \left\{ \begin{array}{l} {e_1} = {z_1} - {y_1}\\ {{\dot z}_1} = {z_2} - {l_1}{e_1}\\ {{\dot z}_2} = {z_3} - {l_2}{e_1} + {b_1}{u_1}\\ {{\dot z}_3} = - {l_3}{e_1} \end{array} \right. $ | (31) |
式中l1, l2, l3为观测器增益, 加入扩张状态量的观测器(31)称为LESO。若观测器增益选为:
| $ [\begin{array}{*{20}{c}} {{l_1}}&{{l_2}}&{{l_3}} \end{array}] = [\begin{array}{*{20}{c}} {{\beta _1}{\omega _{{\rm{1o}}}}}&{{\beta _2}\omega _{1{\rm{o}}}^2}&{{\beta _3}\omega _{1{\rm{o}}}^2} \end{array}] $ | (32) |
可使得s3+β1s2+β2s+β3满足Hurwitz条件。而且可以通过改变β来调整特征根的位置[13], 如将其配置于
| $ {\beta _1} = 3{\omega _{1{\rm{o}}}}, {\beta _2} = 3\omega _{1{\rm{o}}}^2, {\beta _3} = \omega _{1{\rm{o}}}^3 $ | (33) |
式中ω1o为第一个子系统的LESO的观测器带宽。
2.2 LESO收敛性及估计误差分析将(31)中观测器增益取为(33)中对应值, 在做拉氏变换, 可以求得状态变量的估计值z1, z2, z3的传递函数:
| $ \left\{ \begin{array}{l} {Z_1}(s) = \frac{{3{\omega _{1{\rm{o}}}}{s^2} + 3\omega _{1{\rm{o}}}^2s + \omega _{1o}^3}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{Y_1}(s) + \frac{{{b_1}s}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{U_1}(s)\\ {Z_2}(s) = \frac{{(3{\omega _{1{\rm{o}}}}{s^2} + \omega _{1{\rm{o}}}^3)s}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{Y_1}(s) + \frac{{{b_1}(s + 3{\omega _{1{\rm{o}}}})s}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{U_1}(s)\\ {Z_3}(s) = \frac{{\omega _{1{\rm{o}}}^3{s^2}}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{Y_1}(s) + \frac{{{b_1}\omega _{1{\rm{o}}}^3}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{U_1}(s) \end{array} \right. $ | (34) |
定义观测器跟踪误差为:
| $ \left\{ \begin{array}{l} {e_1} = {z_1} - {y_1}\\ {e_2} = {z_2} - {{\dot y}_1}\\ {e_3} = {z_3} - {\xi _1} \end{array} \right. $ | (35) |
又由式(29)知:
| $ {\xi _1} = {x_3} = {{\dot x}_2} - {b_1}{u_1} = {{\ddot y}_1} - {b_1}{u_1} $ | (36) |
因此可以解出误差的传递函数:
| $ \left\{ \begin{array}{l} {E_1}(s) = \frac{{{s^3}}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{Y_1}(s) + \frac{s}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{b_1}{U_1}(s)\\ {E_2}(s) = - \frac{{(s + 3{\omega _{1{\rm{o}}}}){{\rm{s}}^3}}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{Y_1}(s) + \frac{s}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}{b_1}{U_1}(s)\\ {E_3}(s) = - \left[ {1 - \frac{{\omega _{1{\rm{o}}}^3}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}} \right]{s^3}{Y_1}(s) + \\ \;\;\;\;\;\;\;\;\;\;\;\left[ {1 - \frac{{\omega _{1{\rm{o}}}^3}}{{{{(s + {\omega _{1{\rm{o}}}})}^3}}}} \right]{b_1}{U_1}(s) \end{array} \right. $ | (37) |
一般性地将式(37)中输入输出Y1(s), U1(s)取为幅值为K的阶跃信号即Y1(s)=K/s, U1(s)=K/s来对系统的稳态进行分析, 则可求得稳态误差为:
| $ \left\{ \begin{array}{l} {E_{{\rm{ss}}1}}(s) = \mathop {\lim }\limits_{s \to 0} s{E_1}(s) = 0\\ {E_{{\rm{ss2}}}}(s) = \mathop {\lim }\limits_{s \to 0} s{E_2}(s) = 0\\ {E_{{\rm{ss}}3}}(s) = \mathop {\lim }\limits_{s \to 0} s{E_3}(s) = 0 \end{array} \right. $ | (38) |
再考虑LESO的估计误差的动态特性。由(30)和(31)可得LESO对系统(9)的跟踪误差方程:
| $ \dot e = (A - lC)e + E{\xi _1} $ | (39) |
假设作用于此系统的扰动有界, 定义式(39)的状态转移为[22]:
| $ \left\{ \begin{array}{l} {e_1} = \omega _{\rm{o}}^{ - 2}{\eta _1}\\ {e_2} = \omega _{\rm{o}}^{ - 1}{\eta _2}\\ {e_3} = {\eta _3} \end{array} \right. $ | (40) |
式(40)亦可写作:
| $ \mathit{\boldsymbol{e}} = \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \cdot \mathit{\boldsymbol{\eta }} $ | (41) |
其中,e= [e1, e2, e3]T, η= [η1, η2, η3]T, Λ= diag[ωo–2, ωo–1, 1]T。将(41)代入(39)可得:
| $ \frac{1}{{{\omega _{\rm{o}}}}}\mathit{\boldsymbol{\dot \eta }}\mathit{ = }{\mathit{\boldsymbol{A}}_{\rm{o}}}\mathit{\boldsymbol{\eta }}\mathit{ + }\frac{1}{{{\omega _{\rm{o}}}}}E{\xi _1} $ | (42) |
其中:
| $ {\mathit{\boldsymbol{A}}_{\rm{o}}} = \left[ {\begin{array}{*{20}{c}} { - {\beta _1}}&1&0\\ { - {\beta _2}}&0&1\\ { - {\beta _3}}&0&0 \end{array}} \right] $ | (43) |
通过2.1节的配置已使得Ao的特征值均具有负实部:
| $ {\lambda _i}\{ {\mathit{\boldsymbol{A}}_{\rm{o}}}\} = - 1{\rm{ < }}0,i = 1,2,3 $ | (44) |
因此由式(42)不难得出当ω1o增大时总扰动项ξ1的影响会随之减小, 且LESO的跟踪误差逐渐减小。
2.3 子系统的滑模变结构控制器引理1[23] 对于
| $ \dot V(t) \le - \alpha V(t) + \gamma (t), \forall t \ge {t_0} \ge 0 $ | (45) |
的解为:
| $ V(t) \le {e^{ - \alpha (t - {t_0})}}V({t_0}) + \int_{{t_0}}^t {{e^{ - \alpha (t - \tau )}}} \gamma (\tau ){\rm{d}}\tau $ | (46) |
同样以UVMS的第一个子系统为例, 并基于上节所述的总扰动项有:
| $ {{\ddot y}_1} = {b_1}u + {\xi _1} $ | (47) |
定义系统期望输出为y1d, 且假设y1d有界。LESO估计误差为:
| $ s = c\hat e + \dot {\hat e} $ | (48) |
式中c > 0。
基于LESO(31)可建立如下滑模控制器:
| $ u = \frac{{ - ks + {{\ddot y}_{{\rm{1d}}}} - c\dot {\hat e} - {{\hat \xi }_1}}}{{{b_1}}} $ | (49) |
式中
针对系统(47), 选择自抗扰滑模控制器(48)、(49)中的参数k > 1/2, 则其闭环系统的跟踪误差将收敛至某邻域, 且其收敛速度与LESO的参数ωo和k有关。
证明:
引入Lyapunov函数:
| $ V = \frac{1}{2}{s^2} $ | (50) |
由已知可得:
| $ \dot{s}=c\dot{\hat{e}}+\ddot{\hat{e}}=c\dot{\hat{e}}+{{{\ddot{\hat{y}}}}_{1}}-{{{\ddot{y}}}_{1d}}=c\dot{e}+{{b}_{1}}u+{{\xi }_{1}}-{{{\ddot{y}}}_{1d}}+{{{\hat{e}}}_{2}} $ | (51) |
式中
则有:
| $ \dot V = s\dot s = s\left( {c\dot {\hat e} + {b_1}{u_1} + {\xi _1} - {{\ddot y}_{{\rm{1d}}}} + {{\hat e}_2}} \right) $ | (52) |
将式(49)代入(52)有:
| $ \dot V = s(c\dot {\hat e} + {{\ddot y}_{{\rm{1d}}}} - {{\ddot y}_{{\rm{1d}}}} - k\hat s - c\dot {\hat e} + {\xi _1} - {{\hat \xi }_1} + {{\hat e}_2}) $ | (53) |
化简可得:
| $ \dot V = - k \cdot {s^2} + s({\xi _1} - {{\hat \xi }_1} + {{\hat e}_2}) $ | (54) |
可知(54)中
| $ \dot V \le - k \cdot {s^2} + \frac{1}{2}{s^2} + \frac{1}{2}\Delta _{\max }^2 = - (2k - 1)V + \frac{1}{2}\Delta _{\max }^2 $ | (55) |
由引理1可解得:
| $ \begin{array}{l} V(t) \le {e^{ - \alpha (t - {t_0})}}V({t_0}) + \int_{{t_0}}^t {{e^{ - \alpha (t - \tau )}}} \gamma (\tau ){\rm{d}}\tau = \\ {e^{ - (2k - 1)(t - {t_0})}}V({t_0}) + \frac{1}{2}\int_{{t_0}}^t {{e^{ - (2k - 1)(t - \tau )}}} {\rm{d}}\tau = \\ {e^{ - (2k - 1)(t - {t_0})}}V({t_0}) + \frac{1}{2}\int_{{t_0}}^t {{e^{ - (2k - 1)(t - \tau )}}} {\rm{d[}} - (2k - 1)(t - \tau {\rm{)] = }}\\ {e^{ - (2k - 1)(t - {t_0})}}V({t_0}) + \frac{1}{{2(2k - 1)}}\zeta _1^2(1 - {e^{ - (2k - 1)(t - {t_0})}}) \end{array} $ | (56) |
取k > 1/2, 则有:
| $ \mathop {\lim }\limits_{t \to \infty } V(t) \le \frac{1}{{2(2k - 1)}}\Delta _{\max }^2 $ | (57) |
由于V(t) = s2 > 0, 所以当t→∞有:
| $ \mathop {\lim }\limits_{t \to \infty } V(t) = \frac{1}{{2(2k - 1)}}\Delta _{\max }^2 $ | (58) |
可以看到当LESO对扰动的跟踪误差逼近于0, k足够大时:
| $ \mathop {\lim }\limits_{t \to \infty } V(t) = 0 $ | (59) |
因此当k > 1/2时跟踪误差
由以上可知系统的稳定性与收敛速度由滑模参数k和观测器参数ωo决定。其余子系统的控制器及其稳定性可由同样的方法建立与验证。
2.4 微分跟踪器设计考虑当输入信号为非光滑信号时, 避免出现数字计算中的高频振荡, 和为状态变量的提取安排过渡过程, 采用积分链式微分器提取输入信号的微分, 通过每层的积分环节对扰动进行抑制。该有限时间收敛二阶阶微分器(TD)为:
| $ \left\{ \begin{array}{l} {{\dot x}_1} = {x_2}\\ {{\dot x}_2} = - r{\mathop{\rm sgn}} \left( {{x_1} - {v_0}(t) + \frac{{{x_2}\left| {{x_2}} \right|}}{{2r}}} \right) \end{array} \right. $ | (60) |
式中v0(t)为输入信号, 状态量x1在加速度的限制
综上, 完整的滑模自抗扰控制结构图由图 2给出, 图中yd1与yd2分别为参考输入的跟踪信号与其微分信号。其他8个子系统可以以同样的方法建立控制器, 针对AUVMS的完整SM-ADRC的结构图如图 3所示。
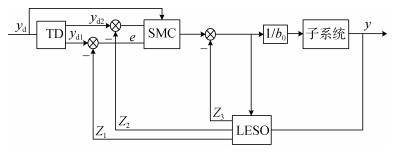 |
| 图 2 SM-ADRC结构图 Fig. 2 Structure of SM-ADRC |
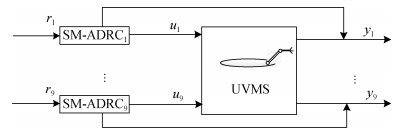 |
| 图 3 UVMS的SM-ADRC结构图 Fig. 3 Frame of SM-ADRC for UVMS |
基于UVMS的工作特点, 在本节对带有两连杆(连接关节n=3)的UVMS的航行轨迹, 机械臂旋转轨迹进行跟踪实验, 测验控制器对UVMS的航向角切换频率要求。并且将实验结果与传统滑模控制, 自抗扰控制进行对比。
在仿真实验中, 9个子系统的LESO的参数分别为ωo=[150, 80, 135, 420, 556, 894, 240, 779, 368]。微分跟踪器参数r均在集合[20, 30]取值, 滑模控制器中参数c在集合[2, 3]中取值, 参数k=[45, 36, 22, 44, 59, 71, 46, 59, 88]对应每个子系统。定义UVMS的初始位置为原点, 即[X, Y, Z] =[0, 0, 0]。为了验证控制器对位置的快速变化的跟踪能力, 将UVMS的机械臂关节角度在0到5秒内期望角度变化轨迹设定为:
| $ \left\{ {\begin{array}{*{20}{l}} {X = ({t^2} - 4.87t + 1)\sin (3t)}\\ {Y = ({t^2} - 4.87t + 1)\sin (4t)}\\ {Z = ({t^2} - 4.87t + 1)\sin (7t)} \end{array}} \right. $ | (61) |
并同时考虑UVMS的位置快速变化时的跟踪效果和航向角变化状态。为了使仿真效果尽可能的接近水下环境, 作者将外部干扰设计为一阶高斯-马尔科夫模型来模拟洋流的运动学特征。其表达式如下:
| $ \left\{ \begin{array}{l} {{\dot v}_{\rm{c}}} = - {\varepsilon _v}{v_{\rm{c}}} + {\omega _v}\\ {{\dot \alpha }_{\rm{c}}} = - {\varepsilon _\alpha }{\alpha _{\rm{c}}} + {\omega _\alpha }\\ {{\dot \beta }_{\rm{c}}} = - {\varepsilon _\beta }{\beta _{\rm{c}}} + {\omega _\beta } \end{array} \right. $ | (62) |
式中vc为设定的洋流速度, αc和βc为洋流的运动方向, εc、εα和εβ为较小的正实数, ωv、ωα和ωβ分别为不同频率的高斯白噪声。
在图 4和图 5中可以看到, 滑模自抗扰控制器可以很好地避免传统滑模控制的抖振现象, 实现更精确的跟踪轨迹, 并且在位置陡然变化时能较传统线性自抗扰控制器和滑模控制器更快的跟踪位置变化, 有更平稳快速的响应过程, 图 5中[Ex, Ey, Ez]分别指代对UVMS的位置[X, Y, Z]的跟踪误差。在图 6中可以看到3个控制器都能跟踪机械臂的摆动角度轨迹进行但在图 7中, [
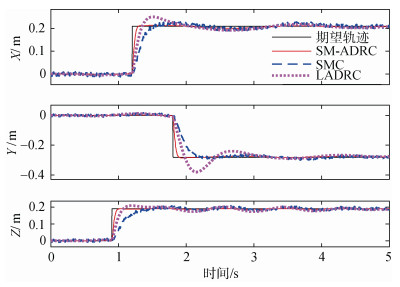 |
| 图 4 UVMS位置变化轨迹 Fig. 4 Trajectory of UVMS's position |
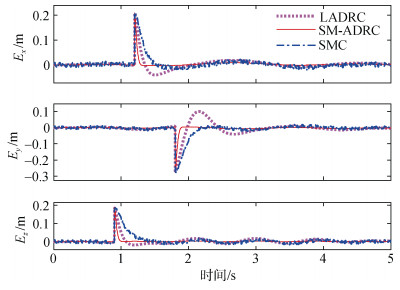 |
| 图 5 UVMS位置跟踪误差 Fig. 5 Error in the UVMS's position tracking |
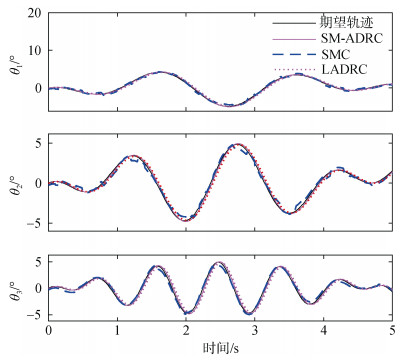 |
| 图 6 机械臂关节角度轨迹跟踪结果 Fig. 6 Angular trajectory tracking of manipulators |
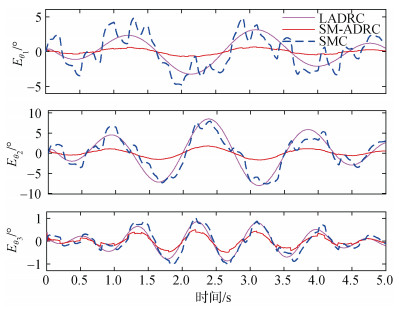 |
| 图 7 UVMS机械臂期望关节角轨迹的跟踪误差 Fig. 7 Error in tracking the UVMS manipulator angular Trajectory |
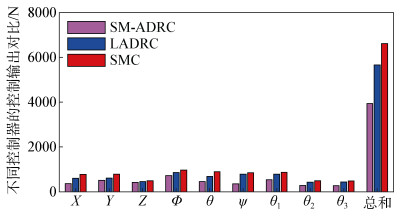 |
| 图 8 不同控制器的控制输出对比 Fig. 8 Comparison of the control outputs of three controllers |
作者提出的滑模自抗扰控制器具有良好的响应过程, 并通过线性扩张观测器对扰动的实时估计, 很大程度上消除了传统滑模控制器的抖振现象。通过滑模控制器代替传统线性自抗扰控制器中的PD控制器, 在系统输入信号快速切换时能保持整个系统的稳定, 并且控制过程中的超调现象大幅度减小, 此外, 作者所设计的控制器与传统滑模控制器和线性自抗扰控制器相比能用更少的控制量达到更好的控制效果, 这在一定程度上保证了所设计的控制器的可进行实际工业化。最后通过仿真实验验证了提出的控制器有效性。
| [1] |
Li X G, Wang H D, Li M, et al. Linear active disturbance rejection controller design for underwater vehicle manipulators with 2-links[C]//Proceedings of 2018 Chinese Automation Congress (CAC). Xi'an: IEEE, 2018: 875-880.
|
| [2] |
Fossen T I. Guidance and control of ocean vehicles[J]. Automatica, 1996, 32(8): 1235. |
| [3] |
Tarn T J, Shoults G A, Yang S P. Underwater robots[M]. US: Springer, 1996: 36-54.
|
| [4] |
Mahesh H, Yuh J, Lakshmi R. A coordinated control of an underwater vehicle and robotic manipulator[J]. Journal of Robotic Systems, 1991, 8(3): 339-370. DOI:10.1002/rob.4620080305 |
| [5] |
Lee M, Choi H S. A robust neural controller for underwater robot manipulators[J]. IEEE Transactions on Neural Networks, 2000, 11(6): 1465. DOI:10.1109/72.883478 |
| [6] |
Huang H, Zhang G C, Li J Y, et al. Model based adaptive control and disturbance compensation for underwater vehicles[J]. Chinese Journal of Mechanical Engineering, 2018, 31(1): 19. DOI:10.1186/s10033-018-0218-5 |
| [7] |
Dai Y, Yu S. Design of an indirect adaptive controller for the trajectory tracking of UVMS[J]. Ocean Engineering, 2018, 151: 234-245. DOI:10.1016/j.oceaneng.2017.12.070 |
| [8] |
Londhe P S, Santhakumar M, Patre B M, et al. Task space control of an autonomous underwater vehicle manipulator system by robust single-input fuzzy logic control scheme[J]. IEEE Journal of Oceanic Engineering, 2017, 42(1): 13-28. |
| [9] |
Wang Y, Jiang S, Chen B, et al. Trajectory tracking control of underwater vehicle-manipulator system using discrete time delay estimation[J]. IEEE Access, 2017, 5: 7435-7443. DOI:10.1109/ACCESS.2017.2701350 |
| [10] |
Huang H, Tang Q, Li H, et al. Vehicle-manipulator system dynamic modeling and control for underwater autonomous manipulation[J]. Multibody System Dynamics, 2016, 41: 125-147. |
| [11] |
韩京清. 自抗扰控制器及其应用[J]. 控制与决策, 1998, 13(1): 19-23. Han Jingqing. Auto disturbances rejection controller and it's applications[J]. Control and Descision, 1998, 13(1): 19-23. |
| [12] |
韩京清. 一类不确定对象的扩张状态观测器[J]. 控制与决策, 1995, 10(1): 85-88. Han Jingqing. The "extended state observer" of a class of uncertain systems[J]. Control and Descision, 1995, 10(1): 85-88. |
| [13] |
韩京清, 王伟. 非线性跟踪--微分器[J]. 系统科学与数学, 1994, 14(2): 177-183. Han Jingqing, Wang Wei. Nonlinear tracking-differentiator. System Science and Mathematics[J]. Journal of Systems Science and Complexity, 1994, 14(2): 177-183. |
| [14] |
Han J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906. DOI:10.1109/TIE.2008.2011621 |
| [15] |
Gao Z Q. Scaling and bandwidth-parameterization based controller tuning[C]//Proceedings of the 2003 American Control Conference, Denver, CO, USA: IEEE, 2003: 4989-4996.
|
| [16] |
Huang Y, Xue W. Active disturbance rejection control:methodology and theoretical analysis[J]. Isa Transactions, 2014, 53(4): 963-976. DOI:10.1016/j.isatra.2014.03.003 |
| [17] |
Kim D, Choi H S, Kim J Y, et al. Trajectory generation and sliding mode controller design of an underwater vehicle manipulator system with redundancy[J]. International Journal of Precision Engineering & Manufacturing, 2015, 16(7): 1561-1570. |
| [18] |
Simetti E, Casalino G. Manipulation and transportation with cooperative underwater vehicle manipulator systems[J]. IEEE Journal of Oceanic Engineering, 2016, 99: 1-18. |
| [19] |
Esfahani H N, Azimirad V, Danesh M. A time delay controller included terminal sliding mode and fuzzy gain tuning for underwater vehicle-manipulator systems[J]. Ocean Engineering, 2015, 107: 97-107. DOI:10.1016/j.oceaneng.2015.07.043 |
| [20] |
Indiveri G. Modelling and identification of underwater robotic systems[M]. Genova: PComput Sci, 1998.
|
| [21] |
Newman J N. Marine hydrodynamics[M]. Cambridge: PMIT Press, 1977.
|
| [22] |
Shao S, Gao Z. On the conditions of exponential stability in active disturbance rejection control based on singular perturbation analysis[J]. International Journal of Control, 2016, 90(10): 2085-2097. |
| [23] |
Ioannous P A, Sun J. Robust adaptive control[M]. Englewood: Prentice-Hal l, Inc, 1995.
|
 2020, Vol. 44
2020, Vol. 44


