中国海洋湖沼学会主办。
文章信息
- 王鑫, 李大鸣, 王兵振, 韩林生. 2020.
- WANG Xin, LI Da-Ming, WANG Bing-Zhen, HAN Lin-Sheng. 2020.
- 点吸收式波浪能俘获装置结构优化方法研究
- THE STRUCTURAL OPTIMIZATION OF POINT ABSORPTION IN WAVE ENERGY CAPTURE DEVICE
- 海洋与湖沼, 51(2): 293-297
- Oceanologia et Limnologia Sinica, 51(2): 293-297.
- http://dx.doi.org/10.11693/hyhz20190900179
文章历史
-
收稿日期:2019-09-22
收修改稿日期:2020-01-19
2. 国家海洋技术中心 天津 300112
2. National Ocean Technology Center, Tianjin 300112, China
点吸收式波浪能装置利用自由浮动的浮子随波浪上下振荡俘获波浪能量, 通过浮子连接的液压装置或机械装置将俘获的波浪能转换机械能, 再通过电机将机械能转换为电能。点吸收式波浪能装置采用相对简便的锚泊式固定, 易于进行从装机功率几千瓦到几百千瓦的系列化设计, 在解决边远海岛、各类海上功能设施供电问题方面具有广泛的应用前景。
由美国海洋电力技术公司研发的波浪发电浮标(Power Buoy)为点吸收式波浪能发电装置的典型代表。目前有单机功率40kW和150kW两种产品, 已基本实现了产品化。国内, 中国科学院广州能源研究所研制与航标形成一体化结构的10W、60W、100W系列化点吸收波浪能发电装置已初步具备产品化条件(王立国等, 2013;王坤林等, 2017;盛松伟等, 2017, 2019);山东大学刘延俊等(2017)在点吸收装置的液压系统、海洋电力技术系统优化等方面取得了丰硕的研究成果。此外, 集美大学、中国海洋大学等科研单位也在点吸收式波浪能装置的研发方面开展了大量有益的工作(罗续业等, 2014;麻常雷等, 2017)。
有关点吸收式波浪能发电装置能量俘获装置的外形, 业内学者已开展了大量的研究工作, 分析对比了长方形、球形、水平圆柱形、垂直圆柱形等多种外形结构。研究结果表明, 垂直圆柱形对于波浪能的吸收和转换最为有利(刘秋林, 2016)。本文即针对垂直圆柱形点吸收式波浪能装置的结构优化方法开展研究。
1 目标海域波浪资源特征分析目标海域的波浪资源特征是开展装置外形优化设计的依据。本文选择威海褚岛北部海域为装置布设目标海域, 并利用布设于该海域的浮标观测数据对该海域的波浪资源特征进行分析, 连续观测时间为2015年1月24日到12月24日, 经统计分析, 出现概率较高的波高和波周期如表 1所示。
|
2-3 | 3-4 | 4-5 | 5-6 | 合计 |
| 0-0.25 | 0.57 | 28.34 | 5.59 | 0.46 | 34.97 |
| 0.25-0.5 | 0.85 | 20.01 | 4.08 | 0.17 | 25.10 |
| 0.5-1.0 | 0.05 | 10.29 | 9.27 | 0.18 | 19.79 |
| 1.0-1.5 | 0 | 0.54 | 7.32 | 0.65 | 8.51 |
| 1.5-2.0 | 0 | 0 | 2.30 | 3.29 | 5.59 |
| 合计 | 1.46 | 59.19 | 28.60 | 8.86 |
可见, 该海域全年以1m以下的小波浪为主, 波周期主要集中在3-5s之间, 其中以3-4s周期波浪最为集中, 低功率的点吸收式波浪能开发利用技术, 正是适合于该目标海域的波浪资源特点的技术形式。
2 点吸收波浪能装置结构关键技术参数分析点吸收式波浪能装置符合弗汝德-克雷洛夫(Froude-Krylov, 简称 F-K)条件, 即入射波动场的波 压强分布不因潜体的存在而改变, 则作用在潜体上 的波浪力一般表达式如公式(1):
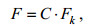 (1)
(1)式中, F为作用在潜体上的波浪力, Fk为未受扰动的入射波压强对浮体的作用力, C为反映附加质量效应的绕射系数, 通常绕射系数需要通过模型试验给予确定。
Fk可分解为入射波作用在整个潜体上的水平作用力和垂直作用力。对于垂直圆柱俘体, 在某一时刻t浮体承受的波浪力的垂直作用力为Fv (何光宇等, 2015;杨绍辉等, 2016a, b ; Tagliabue et al, 2019):
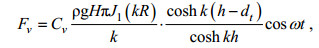 (2)
(2)式中, J1(kR)为零一阶第一类贝塞尔函数, 浮体的半径为R, 浮体高为l, 吃水深度为dt, 其中t为波浪作用到浮体的时间, 水深为h, Cv为垂直绕射系数1.02, ρ为海水密度1.025×103kg/m3, g为重力加速度9.8m/s2, H为波高, k为波数。当t = 0时, Fv等于波浪力的振幅:
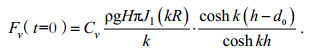 (3)
(3)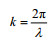
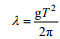
由波浪力垂直分量的计算公式(2)可见, 在特定海域水深条件下, 装置浮子的直径、入水深度两个关键设计参数是装置获能效率的主要决定因素。
3 确定装置浮子直径波浪能发电装置一般包含三个能量转换部分:波浪能俘获系统、机械传动系统、发电机。分析当前波浪能开发利用技术的研究水平, 波浪能俘获系统的能量转换效率一般约为40%, 机械传动系统的工作效率可达到70%, 发电机的合理工作效率为90%, 则当前技术水平下波浪能发电装置的整体能量理想的转换效率η约为:
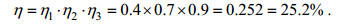 (4)
(4)以低装机功率的装置为研究对象, 设研究目标的装机功率为3kW。发电装置输入端的波浪能功率Pin (单位: kW)需要达到:
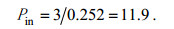 (5)
(5)利用常用的波浪能量简化公式计算波浪能装置所处波浪场的波浪功率密度Pd (单位: kW/m)
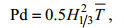 (6)
(6)其中,
H1/3为波浪的有效波高, 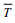
根据波浪资源的分析统计结果, 褚岛海域平均波周期主要分布在3-5s的区间内, 以1m以下小波浪为主, 大部分情况下波高不超过2m。因此选择出现概率较高的波高和波周期为装置的设计输入, 即波浪能装置的设计波高为1m, 波浪平均周期为4s, 这种波况条件下的波浪能功率密度为:
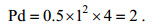 (7)
(7)对于水平截面为圆型的垂直圆柱点吸收波浪能俘获装置来说, 装机3kW的波浪俘获装置的直径D (单位: m)约为:
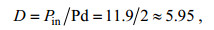 (8)
(8)在此, 将D圆整为6.0m。
4 装置最优吃水深度分析点吸收波浪能装置是通过装置浮子的垂荡运动来获取能量, 即对于垂荡运动, 每个装置都有一个固有周期, 当波浪的周期与该周期相同时, 装置的垂荡运动幅值达到最大, 在该条件下, 波浪能装置的俘获效率达到最大。首先要研究得出装置吃水深度与装置固有周期的对应关系; 进而在资源分析的基础上, 确定目标海域出现频率相对较高的波周期, 以此作为装置固有周期的设计目标, 并通过固有周期与装置吃水深度的对应关系计算出装置的最佳吃水深度。本文对点吸收装置固有周期与装置浮子吃水深度的对应关系分析借助AQWA软件, 计算前文分析得出的6m直径浮子不同吃水深度对应的装置固有周期, 进而分析得出二者的对应变化关系。
4.1 计算方法验证利用AQWA计算张亮等(2015a)的一个例子, 将本文采用计算方法得出的结果与算例结果进行比较, 以验证本文算法的合理性。
计算为一种圆柱形点吸式波浪能装置, 如图 1所示。俘获装置的外径为6m, 内孔直径为2m, 高度为1.6m, 静止状态下吃水深度为0.68m。装置的质量为17.517t。
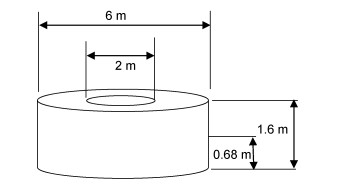 |
| 图 1 计算的点吸收装置外形尺寸 Fig. 1 The calculated overall dimensions of the point absorber |
在利用软件建立模型的过程中, 将全局坐标系的x-y平面与静水面重合, x轴与波浪传播的方向平行, 方向与波浪传播方向相反; z轴与铅锤方向平行, 竖直向上; 坐标原点位于水线面的形心处。模型水下深度根据考察对象的具体数值进行设定, 水线以上的高度设定为1.0m。模型的质量按模型的排水量估算, 为保证运动的稳定性, 将模型的重心设定在浮心下面100mm处。
在此基础上, 利用ANSYS mesh模块生成俘获装置表面网格单元, 装置网格划分情况如图 2所示, 最大单元尺寸设置为0.2m, 共计9920个单元, 网格类型采用程序默认设(De O Falcão, 2009; Lopes et al, 2009; Penalba et al, 2017)。最大允许波频率为1.14Hz, 计算过程中采用规则波, 入射波浪的周期范围为2.4-5s。初始入水深度0.5m, 俘获装置初始静平衡状态处于竖直位置。水线面将浮子模型分为上下两部分, 只有水下部分参与水动力绕射计算。
 |
| 图 2 计算网格 Fig. 2 The computational grid |
在实际工作过程中, 点吸收装置以垂直方向的垂荡运动为主, 在导柱的限制下其他方向的往复振荡和摆动的幅度很小。因此, 在计算模型中为限制绕三个坐标轴的摇摆运动, 特别是绕y轴的摇摆运动, 设置了绕3个坐标轴摇摆运动的较大数值的阻尼。
波浪能俘获装置的垂荡运动响应幅值比的计算结果如图 3所示。图中, 横轴为入射波浪的周期, 纵轴为装置垂荡运动响应幅值比。由图 3可知, 装置在波周期为3.1s时的垂荡响应幅值最大, 即装置的固有周期为3.1s。
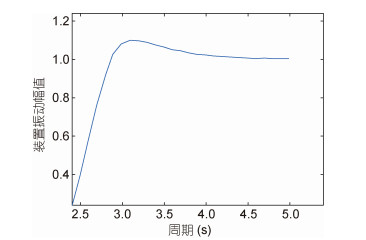 |
| 图 3 算例装置振荡幅值与周期关系 Fig. 3 Relationship between oscillation amplitude and period of numerical example device |
文献的计算结果如图 4所示, 该计算结果同样表明装置在波周期为3.1s时垂荡运动响应达到最大, 且对照垂荡运动响应随波浪周期的变化趋势与本文计算的结果, 两者近似相同(张亮等, 2015a, b ; 郑雄波, 2016)。这说明本文建立的计算模型合理可行, 应用该方法进行圆柱型点吸收式装置的波浪能转换特性计算可有效支撑浮子吃水深度与装置固有周期对应关系的分析。
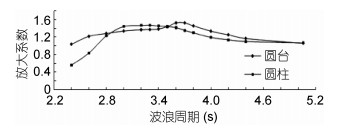 |
| 图 4 文献中算例的计算结果 Fig. 4 The calculation results of numerical examples in literature 注:张亮等, 2015a |
考察了初始吃水深度对圆柱形点吸收式波浪能俘获装置固有周期的影响, 计算过程中装置的外径均为6m, 参照国内点吸收波浪能装置的设计经验, 水面以上部分的高度均取为1m (林江波, 2006;史宏达等, 2011, 2017)。开展以下9组计算, 得到不同浮子吃水深度下的装置固有周期, 计算结果分布要能够覆盖目标海域波周期主要的分布区间, 即3-5s。计算工况相关参数如表 2, 各工况中装置浮心位置均位于水下部分的中心, 重心位置位于浮心位置正下方, 两者相距0.1m。计算结果如图 5、表 3所示。
| 组别 | 入水深度(m) | 装置质量(×104kg) | 装置绕x、y轴的转动惯量[×105(kg·m2)] | 装置绕z轴的转动惯量[×105(kg·m2)] |
| 1 | 0.5 | 1.449 | 0.345 | 0.652 |
| 2 | 0.6 | 1.739 | 0.422 | 0.783 |
| 3 | 0.8 | 2.319 | 0.587 | 1.043 |
| 5 | 1.6 | 4.637 | 1.495 | 2.087 |
| 6 | 2.0 | 5.796 | 2.162 | 2.608 |
| 7 | 2.5 | 7.245 | 3.271 | 3.260 |
| 8 | 3.0 | 8.694 | 4.750 | 3.912 |
| 9 | 3.5 | 1.014 | 6.674 | 4.565 |
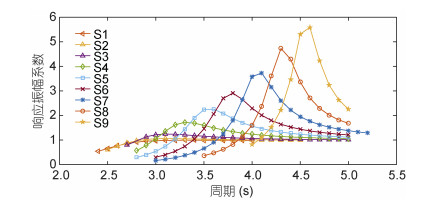 |
| 图 5 工况1至9周期与响应振幅系数关系 Fig. 5 Relationship between period and response amplitude coefficient in operation conditions 1 to 9 |
| 组别 | 浮子吃水深度(m) | 装置固有周期(s) |
| 1 | 0.5 | 3.3 |
| 2 | 0.6 | 3.1 |
| 3 | 0.8 | 3.1 |
| 4 | 1.2 | 3.3 |
| 5 | 1.6 | 3.6 |
| 6 | 2.0 | 3.8 |
| 7 | 2.5 | 4.1 |
| 8 | 3 | 4.3 |
| 9 | 3.5 | 4.7 |
根据表 3, 利用插值法绘制装置浮子吃水深度和固有周期对应关系曲线(图 6), 横轴为吃水深度, 纵轴为固有周期。
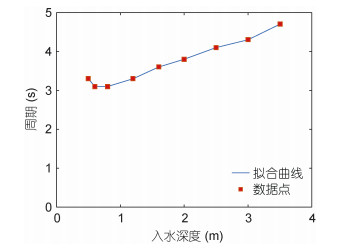 |
| 图 6 装置浮子吃水深度和固有周期对应关系曲线 Fig. 6 Correspondence relation between the draft and natural period of the floater |
根据对目标海域波浪能资源特征的分析, 该海域全年3-5s周期的波浪出现的概率最大, 其中以3-4s周期波浪最为集中, 装置固有周期设计为4s可最大限度的获得波浪能量, 根据分析得出的浮子吃水深度和固有周期的对应关系, 可得出在目标海域波浪能资源条件下, 装置的最优吃水深度为2.44m。
至此, 根据目标海域波浪能资源特性, 对圆柱形浮子点吸收波浪能转换装置的外形关键技术参数的优化设计完成, 既直径6m, 固有周期4s, 最优吃水深度2.44m。
5 结论本文在充分掌握目标海域波浪能资源特性的情况下, 研究了对点吸收波浪能俘获装置结构进行优化的方法, 并重点关注点吸收装置浮子直径和吃水深度的分析和确定方法。通过研究可得出以下结论:根据弗汝德-克雷洛夫定律分析, 在所处水深确定的情况下, 点吸收波浪能装置浮子的直径和吃水深度是其关键参数, 是装置能量俘获能力的重要决定因素。对点吸收波浪能装置结构的优化方法研究, 即是对两个参数在目标海域环境条件下最优值的研究确定。通过计算可以得到浮子吃水深度和浮子固有周期之间的对应关系; 分析装置目标布置海域的波浪资源特征, 可得到出现概率最高, 也即“蕴含波浪能量”最多的波浪周期值, 该值即为点吸收装置的设计目标固有周期, 与之对应浮子吃水深度即为装置的最优吃水深度, 最终得出装置外形结构的优化设计方案。该方法可应用于大多数圆柱形点吸收装置的外形结构优化设计工作。
王立国, 游亚戈, 张亚群, 等. 2013. 波浪能发电装置动力摄取系统研究进展. 机床与液压, 41(1): 165-168, 162 DOI:10.3969/j.issn.1001-3881.2013.01.046 |
王坤林, 盛松伟, 叶寅, 等. 2017. 波浪能装置中液压发电系统Boost变换机理及控制策略. 电力系统自动化, 41(12): 173-178 DOI:10.7500/AEPS20161111003 |
史宏达, 曲娜, 曹飞飞, 等. 2017. 振荡浮子波能发电装置浮子运动性能的试验研究. 中国海洋大学学报, 47(6): 124-130 |
史宏达, 刘栋, 刘臻. 2011. 一种新型波能发电装置的运动响应计算. 中国海洋大学学报, 41(10): 111-116 |
刘延俊, 贺彤彤. 2017. 波浪能利用发展历史与关键技术. 海洋技术学报, 36(4): 76-81 |
刘秋林, 2016.点吸收浮子阵列的波能转换特性研究.北京: 清华大学博士学位论文, 23-67
|
杨绍辉, 何宏舟, 陈沪, 等. 2016a. 阵列筏式波浪能发电系统设计与试验研究. 机械工程学报, 52(11): 57-62 |
杨绍辉, 何宏舟, 李晖, 等. 2016b. 点吸收式波浪能发电技术的研究现状与展望. 海洋技术学报, 35(3): 8-16 |
何光宇, 杨绍辉, 何宏舟, 等. 2015. 阵列式波浪能发电装置的水动力分析. 水力发电学报, 34(2): 118-124 |
张亮, 国威, 王树齐. 2015a. 一种点吸式波浪能装置水动力性能优化. 哈尔滨工业大学学报, 47(7): 117-121 |
张亮, 国威, 郑雄波. 2015b. 圆柱浮子垂荡运动性能的CFD模拟与流场分析. 华中科技大学学报(自然科学版), 43(12): 65-70 |
林江波, 2006.浮子式海浪发电船的动态分析与仿真.秦皇岛: 燕山大学硕士学位论文, 20-35
|
罗续业, 夏登文. 2014. 海洋可再生能源开发利用战略研究报告. 北京: 海洋出版社, 72-81
|
郑雄波, 2016.两类点吸式波能装置水动力特性研究.哈尔滨: 哈尔滨工程大学博士学位论文, 42-56
|
盛松伟, 王坤林, 吝红军, 等. 2019. 100 kW鹰式波浪能发电装置"万山号"实海况试验. 太阳能学报, 40(3): 709-714 |
盛松伟, 张亚群, 王坤林, 等. 2017. 波浪能发电装置能量转换系统多级负载试验. 可再生能源, 35(2): 311-316 |
麻常雷, 夏登文, 王海峰. 2017. 国内外海洋能进展及前景展望研究. 北京: 海洋出版社, 56-70, 121-132
|
De O Falcão A F, 2009. Wave energy utilization:a review of the technologies. Renewable and Sustainable Energy Reviews, 14(3): 899-918 |
Lopes M F P, Hals J, Gomes R P F et al, 2009. Experimental and numerical investigation of non-predictive phase-control strategies for a point-absorbing wave energy converter. Ocean Engineering, 36(5): 386-402 DOI:10.1016/j.oceaneng.2009.01.015 |
Penalba M, Touzón I, Lopez-Mendia J et al, 2017. A numerical study on the hydrodynamic impact of device slenderness and array size in wave energy farms in realistic wave climates. Ocean Engineering, 142: 224-232 DOI:10.1016/j.oceaneng.2017.06.047 |
Tagliabue A, Izzo L, Mella M, 2019. Absorbed weak polyelectrolytes:impact of confinement, topology, and chemically specific interactions on ionization, conformation free energy, counterion condensation, and absorption equilibrium. Journal of Polymer Science Part B:Polymer Physics, 57(9): 491-510 |
 2020, Vol. 51
2020, Vol. 51


