中国海洋湖沼学会主办。
文章信息
- 陈子飞, 任强, 胡贺岗, 陈永华, 王蓓, 于非, 南峰, 王建丰, 唐瑛. 2022.
- CHEN Zi-Fei, REN Qiang, HU He-Gang, CHEN Yong-Hua, WANG Bei, YU Fei, NAN Feng, WANG Jian-Feng, TANG Ying. 2022.
- 南海西北部半日内潮参量次谐频不稳定生成的近惯性波研究
- SEMIDIURAL TIDE PARAMETETRIC SUBHARMONIC INSTABILITY INDUCED NEAR-INERTIAL WAVES IN NORTHWESTERN SOUTH CHINA SEA
- 海洋与湖沼, 53(1): 62-73
- Oceanologia et Limnologia Sinica, 53(1): 62-73.
- http://dx.doi.org/10.11693/hyhz20210800174
文章历史
-
收稿日期:2021-08-02
收修改稿日期:2021-09-11
2. 中国科学院大学 北京 100049;
3. 中国科学院 海洋环流与波动重点实验室 山东青岛 266071;
4. 中国科学院海洋大科学研究中心 山东青岛 266071;
5. 青岛海洋科学与技术试点国家实验室 海洋动力过程与气候功能实验室 山东青岛 266237
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. CAS Key Laboratory of Ocean Circulation and Waves, Chinese Academy of Sciences, Qingdao 266071, China;
4. Center for Ocean Mega-Science, Chinese Academy of Sciences, Qingdao 266071, China;
5. Marine Dynamic Process and Climate Function Laboratory, Pilot National Laboratory for Marine Science and Technology (Qingdao), Qingdao 266237, China
海洋内部混合主要是由内波破碎驱动(Waterhouse et al, 2014; Whalen et al, 2020)。潮流与地形相互作用生成内潮, 内潮为内波场提供约0.9 TW的能量, 是内波场能量重要的一部分, 对于维持大洋层结、经向翻转环流具有重要的意义(Munk et al, 1998)。
内潮生成后, 高模态内潮在当地耗散, 而低模态内潮则向远距离传输。Vic等(2019)表明≥4模态的内潮能量与微结构探头观测到的耗散能量是相一致的, 因此, ≥4模态的内潮能量主要是在生成区耗散。而低模态内潮离开生成区, 向远处传播时与复杂地形之间的相互作用是低模态内潮能量向耗散尺度传递的一个通道(Kelly et al, 2013; De Lavergne et al, 2019)。除此之外, 波-波间非线性相互作用也是低模态内潮能量向高模态传递的重要机制(MacKinnon et al, 2013; Ansong et al, 2018; Onuki et al, 2018; De Lavergne et al, 2019)。内波间的非线性能量传递通常用三波共振理论来研究, 当三波间的波数满足ω1±ω2=ω0, 频率满足k1±k2=k0时, 三波间的共振最为显著, 能量传递最为有效(MacKinnon et al, 2013)。
参量次谐频不稳定(parametric subharmonic instability, PSI)是非常重要的一种波-波间非线性三波共振相互作用, 是指频率几乎相同且垂向波数几乎相反的两个高模态子波(daughter waves)与另外一个频率为前者两倍的低模态母波(primary wave)之间的相互作用(Müller et al, 1986)。当内潮位于临界纬度时, 子波频率等于当地惯性频率, 低模态内潮向高模态内波能量的转移最为有效, 为混合提供能量(MacKinnon et al, 2005)。临界纬度是指内潮频率是惯性频率2倍的纬度, M2 (太阴主要半日分潮)和S2 (太阳主要半日分潮)内潮的临界纬度分别为28.8°N和29.9°N。又由于内潮总能量中约2/3是半日频(D2)内潮(Munk et al, 1998; Egbert et al, 2000; Nycander, 2005), 所以研究半日内潮PSI过程对研究海洋内部混合是相当重要的。
PSI过程也发生在临界纬度向赤道以内区域。模式结果表明半日内潮发生显著PSI过程的纬度范围在25°~30°N, 半日内潮的能量通过其水平速度梯度的非线性平流项快速地向半频谐波(D1, 即全日频)转移(MacKinnon et al, 2005)。Ansong等(2018)通过模式结果表明中尺度涡和风生近惯性波(near-inertial wave, NIW)会对PSI过程产生影响, PSI在纬向上会出现更宽的分布特征。数值模式表明, PSI过程也可以生成不等于母波频率一半的子波(Korobov et al, 2008), 因此在非临界纬度上PSI过程生成的近惯性波是可能发生的。当在非临界纬度地区时惯性频率不再等于D1频率, PSI的共振系统可以由频率为f、D2-f和D2的三波组成。Xie等(2011)基于南海118.41°E, 20.58°N的潜标资料研究半日内潮PSI过程, 结果表明半日内潮不仅生成D1频内波, 也首次发现由PSI过程生成的NIW。
目前为止, 虽然对PSI过程生成的半频谐波(D2=D1+D1)已有较多研究(MacKinnon et al, 2013; De Lavergne et al, 2019), 但对非临界纬度上PSI过程生成的近惯性波(D2=f+D2-f )研究还是较少, 对其引起的混合还未给出定量的认识。本文基于国家重点研发项目的准实时传输深海潜标系统, 主要研究南海西北部半日内潮PSI过程生成的NIW并通过参数化方法给出混合的时间分布特征。
1 数据和方法 1.1 数据2020年11月20日, 搭载向阳红14科考船, 在南海西北部陆坡114.01°E, 18.45°N, 水深为约2 290 m位置布放准实时潜标(图 1)。2021年5月27日, 搭载海洋地质4号科考船, 对潜标成功回收。
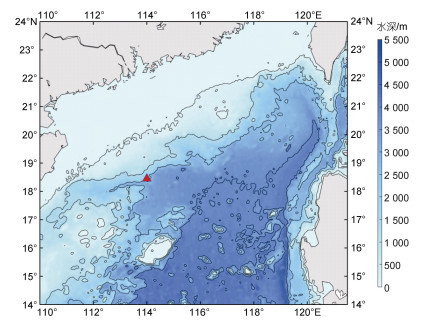 |
| 图 1 潜标布放位置及地形分布 Fig. 1 Position of subsurface mooring and bathymetry distribution 注: 红色三角表示潜标位置 |
潜标系统包括中科院声学研究所研发的4台75 kHz声学多普勒流速仪(acoustic doppler current profilers, ADCP), 自然资源部国家海洋技术中心生产的22台温盐深仪(conductivity temperature depth, CTD)和11台感应耦合温度仪(temperature, T), 可以实现近乎全水深的温度、盐度、流速连续观测。潜标系统仪器的详细配置信息见表 1。
| 仪器 | 仪器数量/台 | 配置深度/m | 采样间隔/s |
| 声学多普勒流速仪ADCP | 4 | 540(上打); 540(下打); 1 540(上打); 1 540(下打) | 3 600 |
| 感应耦合温盐深仪CTD | 22 | 50; 90; 130; 170; 210; 250; 290; 330; 380; 450; 490; 550; 590; 690; 790; 990; 1 190; 1 390; 1 530; 1 590; 1 990; 2 030; | 3 600 |
| 感应耦合温度仪T | 11 | 70; 110; 150; 190; 230; 270; 310; 350; 420; 890; 1 790 | 3 600 |
本文关注的是上层500 m的半日内潮PSI过程, 因此只采用一台位于540 m处向上打的ADCP流速数据。ADCP原始数据垂向分辨率为16 m, 采样间隔为1 h, 在计算垂向速度剪切时, 将原始数据线性插值成垂向分辨率为10 m的标准网格数据。为了排除风生近惯性波对PSI生成近惯性波的干扰, 尤其是台风过程, 本文选择2021年2月1日至2021年4月21日的观测数据, 对该时段进行谱分析。由于在该时间内仍然存在大风过程对PSI过程生成近惯性波信号的污染, 所以再从该时间长度内选择两个无风干扰的时段开展半日内潮PSI过程生成近惯性波分析, 一段为2021年2月5~25日(后文称该时段为T1), 另一段为2021年3月27日至4月16日(后文称该时段为T2)。
除此之外, 本文还用到ETOPO1的地形数据, https://ngdc.noaa.gov/mgg/global/global.html, NCEP/DOE提供的6 h分辨率的风应力数据, https://psl.noaa.gov/data/gridded/data.ncep.reanalysis2.html。
1.2 方法 1.2.1 双相干谱双相干谱是一种高阶谱分析方法, 已被广泛地应用于区分非线性耦合波和独立存在的波(Kim et al, 1979; Carter et al, 2006; Xie et al, 2011, 2013, 2016, 2021; MacKinnon et al, 2013)。该方法可以分析三波共振中生成相位相干的波, 假设Xk是流速时间序列数据u(t)的傅里叶变换,
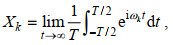 (1)
(1)式中, T是时间长度, ωk=2πk/T, 则双谱B可以定义为, B(k, l)= E[Xk Xl Xk+l*], E[ ]表示数学期望, *表示复共轭。如果ωk, ωl, ωk+l三个频率的波之间相互独立, 则它们的双谱为0; 若其中一个波是由其他波之间非线性耦合产生, 则它们的双谱不为0。
双谱标准化之后可以消除振幅对双谱值的影响, 得到双相干谱,
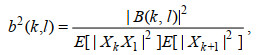 (2)
(2)标准化后, 0≤b (k, l)≤1。理论上, 当双相干值b不等于0时表示三个波之间有一定程度的相位相干, 但在实际中超出显著水平的双相干值是有必要的。根据蒙特卡洛模拟, Elgar等(1998)给出双相干值的置信度, 80%= (3.2/ndof)1/2, 90%= (4.6/ndof)1/2, 95%= (6/ndof)1/2, nnot表示自由度数, 是独立样本的2倍。本文中, 将T1和T2时间序列均分成11个独立的时间段, 每个时间段重叠50%, 数据长度大约为3 d, 自由度数为22, 所以, 80%、90%、95%的置信水平分别为0.38、0.46、0.52。
1.2.2 平板模型平板模型可以计算混合层对当地风场强迫的响应(Pollard et al, 1970)。通过输入风应力τ和混合层深度H可以得到响应风应力的混合层内流速,
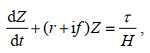 (3)
(3)式中, Z =u +iv是混合层内x, y方向的流速, τ=τx +iτy表示x, y方向的风应力, f为科氏频率, H=50 m, t为时间。混合层流速可以表示为Ekman流与近惯性流的和, 即Z=ZI+ZE。模型中r为惯性运动在传播过程中的衰减系数, 其随频率σ而变化, r(σ)=r0[1-exp (-σ2/2σc2)], r0=0.15f, σc=0.5f。因此不能再通过时间离散求解上述方程, Alford (2003)基于谱方法和输入NCEP 6 h分辨率的再分析风应力数据求解平板模型, 模型结果得到改进, 且更适用于高纬度地区。对风应力进行傅里叶变换, (3)式的解R(σ)≡Z(σ)/T(σ)为
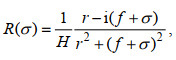 (4)
(4)Ekman分量为
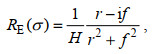 (5)
(5)则惯性分量为RI=R–RE, 混合层内惯性流速的频域解为ZI (σ)=RI (σ) T(σ), 再通过傅里叶逆变换得到时域解。最后得到风向海洋混合层内输入的近惯性能量通量(wind-generated near-inertial energy flux, WGEF)为Re[Zτ*]。
1.2.3 Gregg-Henyey-Polzin (GHP)细尺度参数化方法由于湍流微结构观测难度大、成本高, 多种估算海洋混合的方法应运而生。陈子飞等(2021)基于在吕宋海峡观测到的23个微结构湍流剖面仪和细尺度观测数据, 对GHP细尺度参数化、Mackinnon and Gregg (MG)参数化和Thorpe尺度方法进行比较研究, 评估它们的适用性, 发现GHP参数化方法估算湍流混合最优。GHP细尺度参数化方法也广泛地应用于估算大洋内部混合(Henyey et al, 1986; Gregg, 1989; Polzin et al, 1995; Kunze et al, 2006; Waterhouse et al, 2014)。刻画海洋混合的两个关键参数是湍动能耗散率ε和扩散率κ, ε可以由流速垂向剪切和浮力频率参数化:
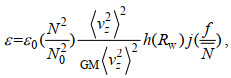 (6)
(6)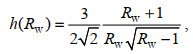 (7)
(7)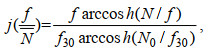 (8)
(8)式中, ε0=4.7×10-10 W/kg, f30=f(30°N), N表示浮力频率, N0=5.2×10-3 rad/s, 〈vz2〉表示垂向剪切方差, GM〈vz2〉表示通过大洋内波GM (Garrett-Munk)谱计算的剪切方差(Garrett et al, 1972)。Rw=7, 表示浮力频率标准化后的剪切方差与应变方差比(Kunze et al, 2006)。
与Kunze等(2006)相一致, 本文采用320 m长度的垂向流速剪切和浮力频率数据计算浮力频率标准化的剪切方差〈vz2〉/N2。首先通过10 m垂向分辨率、采样间隔为1 h的规则网格化ADCP流速数据得到垂向速度剪切。由于GHP方法不适用于混合层内的混合估算, 选择106~426 m范围的剪切数据和该深度内平均的浮力频率对剪切进行标准化, 得到vz/N。然后对该深度内的vz/N做谱分析得到剪切谱S[vz/N], 最后从最小波数kmin=2π/180 m积分至最大波数kmax=2π/60 m得到〈vz2〉/N2 (Sheen et al, 2013, 2015),
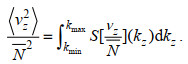 (9)
(9)GM谱的剪切方差在相同波数段积分得到,
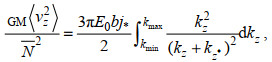 (10)
(10)式中, kz* = πjN/bN0, j*=3, b=1 300 m, E0 =6.3 × 10-5。
扩散率则可以通过湍动能耗散率和浮力频率表示, κ=Γε/N2, Γ为通量系数, 在大洋中Γ取0.2 (Osborn, 1980)。
2 结果 2.1 内波速度谱图 2是内波的速度谱。图 2a为98~498 m深度平均的速度功率谱, 结果显示在半日(D2)和全日(D1)频出现显著的能量峰值且D1能量占优。在大洋中, 半日内潮能量相对全日内潮能量占优势, 但在南海北部则以全日内潮能量占优势(Duda et al, 2008; De Lavergne et al, 2019)。另外, D3 (频率为一天3次的周期运动)上也出现峰值。D3频峰值可能来源于D1和D2之间的非线性过程, 且这种非线性过程主要受水平流速的垂向、水平梯度控制(管守德, 2014)。由于PSI过程生成的次级谐波具有高模态、强垂向剪切的特征, 因此D1和D2之间发生非线性过程的垂向剪切很有可能是由半日内潮PSI过程产生的高模态D1内波提供的。图 2b和图 2c分别是226 m和386 m深度上的速度功率谱, 结果显示在f (惯性频)和D2-f (半日减惯性频)出现显著的峰值。但需要注意的是, 226 m深度上的惯性峰值出现些许的蓝移, 与之相对应的D2-f则出现些许的红移。与深度平均的能谱不同, 图 2b和图 2c显示惯性频能量与全日频能量相当, D2-f频能量与半日频能量相当, 表明这些深度上的惯性能量和D2-f能量与内潮能量是同等重要的。接下来需要对这三个频段内的流速和能量进行比较分析。
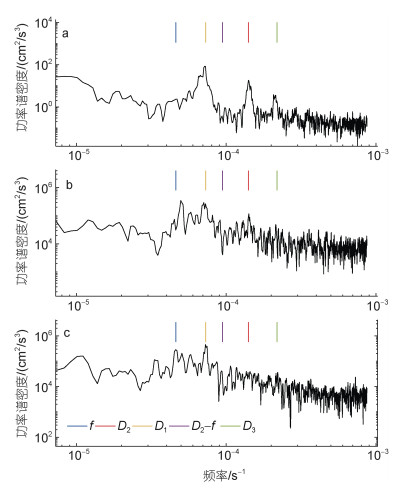 |
| 图 2 速度功率谱密度 Fig. 2 Power spectral density of velocity 注: a: 98~498 m深度平均的速度功率谱密度; b: 深度为226 m速度功率谱密度; c: 深度为386 m的速度功率谱密度; 近惯性、D2-f和D2运动的滤波频率区间分别为[0.90 1.20]f、[0.60 0.74]/12.42h、[0.9 1.15]/12.42h; f、M2、D1、D2-f、D3分别表示惯性、半日、全日、半日减惯性和三分之一日频率 |
根据内波谱(图 2), 近惯性、D2-f和D2运动的滤波区间分别为[0.90 1.20]f、[0.60 0.74]/12.42 h、[0.9 1.15]/12.42 h, 对原始流速带通滤波后得到T1时段内的近惯性的流速和动能、D2-f的流速和动能以及半日内潮的流速和动能(图 3)。图 3a显示近惯性流速具有较小的垂向尺度(即高垂向模态)和无规则的相位分布, 与上传的风生近惯性波相位特征存在显著的区别, 表明T1段内的近惯性运动可能与风生近惯性波无关。图 3c是D2-f流速, 其垂向尺度较小但相比于近惯性运动具有较大的垂向尺度, 其流速幅值相比于近惯性运动也较弱。图 3b和图 3d显示近惯性动能增强的深度与D2-f动能增强的深度是相对应的, 如2月5~12日约230 m、2月11日~14日约120 m、2月11~20日约350 m等。图 3e和图 3f是半日内潮D2的流速与动能, D2运动具有更大的垂向尺度(即低垂直模态), 表明其垂向剪切较D2-f和近惯性运动较弱。另外, 近惯性和D2-f运动增强的时间与强半日内潮动能的时间是相对应的, 这是因为非线性三波共振属于强非线性相互作用, 母波的幅值越大, 能量转移越快速(Xie et al, 2011; MacKinnon et al, 2013)。综上可知, T1时段内的半日内潮运动具有低模态的特征, 近惯性和D2-f运动具有高模态的特征, 强半日潮运动期间会生成显著增强的近惯性和D2-f运动, 且生成的近惯性和D2-f运动在深度和时间上是相对应的。
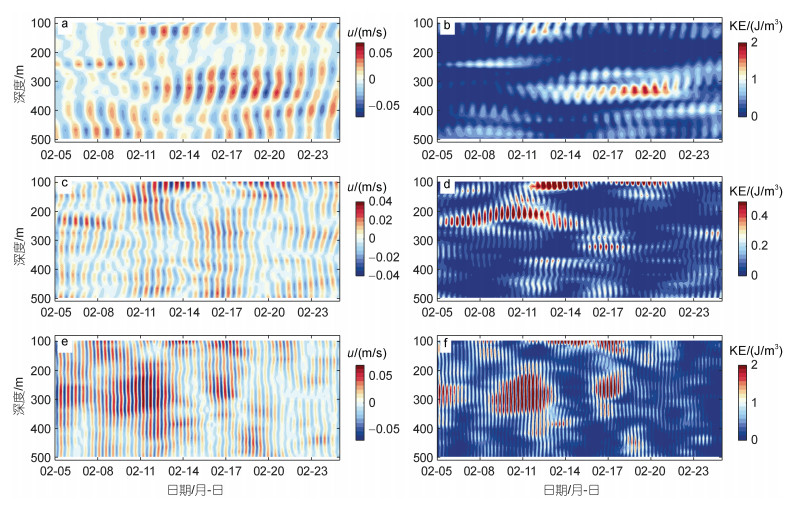 |
| 图 3 T1期间流速u与动能KE深度时间序列 Fig. 3 Depth-time plot of velocity and kinetic energy during T1 注: a: 近惯性纬向流速; b: 近惯性动能; c: D2-f纬向流速; d: 动能; e: 半日潮纬向流速; f: 半日潮动能; D2-f与f和D2的颜色图范围是不一致的; u表示流速, KE表示动能(kinetic energy) |
图 4是T2时段内的近惯性、D2-f和半日潮流速与动能。总体上, 三种频带的运动与T1期间具有相似的特征。首先, 近惯性和D2-f具有高模态的特征(图 4a和图 4b), 相比于半日内潮运动的垂向尺度较小(图 4e); 其次, 强近惯性与D2-f动能出现在强半日内潮期间(图 4b、图 4d和图 4f)。但也存在一些差异, 一是T2时段内的半日内潮相比于T1时段内较弱(图 4e), 所以对应着的近惯性、D2-f运动也较弱; 二是显著发生近惯性和D2-f运动的深度要更靠近表层, 基本上位于约150 m以上。
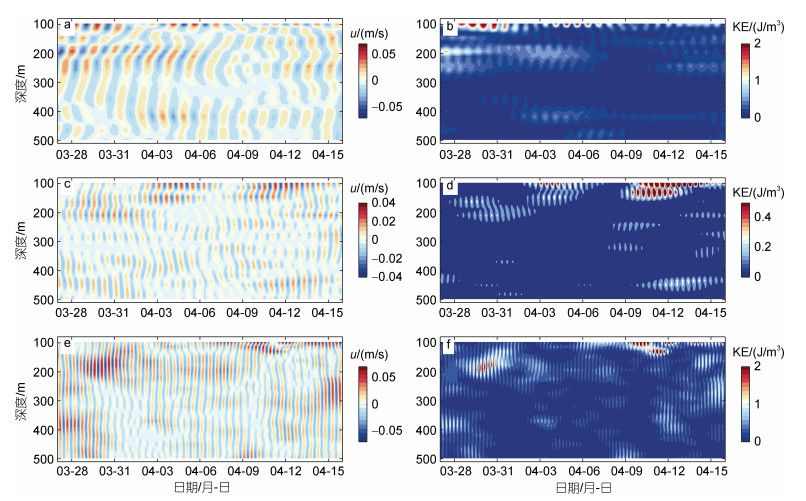 |
| 图 4 T2期间的速度u和动能深度时间序列 Fig. 4 Depth-time plot of velocity and kinetic energy during T2 注: a: 近惯性纬向流速; b: 近惯性动能; c: D2-f纬向流速; d: 动能; e: 半日潮纬向流速; f: 半日潮动能; u和KE (kinetic energy)表示流速和动能 |
通过能谱与两个时间段内的流速和动能结果初步表明潜标观测到的近惯性和D2-f运动可能是来自于半日内潮PSI过程。下一章节将讨论两个时段内的近惯性能量与风场的关系, 利用双相干谱分析方法分析三波间的非线性相互作用并讨论引起海洋混合的时间变化。
3 讨论 3.1 近惯性运动与风场的关系风对表层海水的做功是上层海洋近惯性运动最重要的能量来源(Alford et al, 2001, 2016)。平板模型可以有效地模拟混合层对风场的响应(Alford et al, 2012)。图 5a是NCEP/DOE提供的6 h分辨率在T1期间的风应力, 输入平板模型后得到风生混合层内近惯性能量通量(WGEF, 图 5b)。为了给出潜标观测到的近惯性运动与风场的关系, 图 5b给出潜标观测到的98 m深度上的近惯性动能(near-inertial kinetic energy, NIKE)。如果观测到的近惯性动能是来自于风场向混合层内输入的能量, 那么近惯性动能和风生近惯性能量间将会有较好的线性关系, 即当WGEF增加时, NIKE也会增加; 反之亦然。图 5b显示在T1期间近惯性动能与风生近惯性能量的增长和减弱并不能很好地对应, 表明T1时段内潜标观测到的近惯性动能并非是主要来自于风生近惯性动能, 该结论与图 3a分析是相一致的。
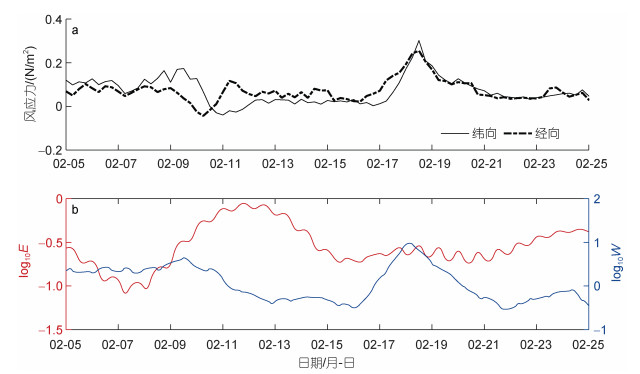 |
| 图 5 T1期间风应力、风生混合层内近惯性能量与近惯性动能 Fig. 5 Wind stress, wind generated near inertial energy flux in mixed layer and near inertial kinetic energy during T1 注: a: 风应力时间序列; b: 风生混合层内近惯性能量通量(W, 单位: J/m3; 蓝线)和近惯性动能(E, 单位: mW/m2; 红线) |
图 6是T2期间的风生近惯性能量与潜标观测到的近惯性动能的比较, 与T1期间结论相同, 近惯性动能与风生近惯性能量的增长和减弱并不能很好地对应, 所以T2时段内观测到的近惯性动能也并非是主要来自于风生近惯性动能, 这与图 4a中不规则的近惯性流速相位是相一致的。另外, 为了量化WGEF与NIKE之间的关系, 两者的相关系数在这里被给出来。T1时段内的相关系数是R=-0.28, T2时段内的相关系数是R=0.05。可见, 两个时段内的相关系数都较低, 进一步说明观测到的NIKE与风场无关。
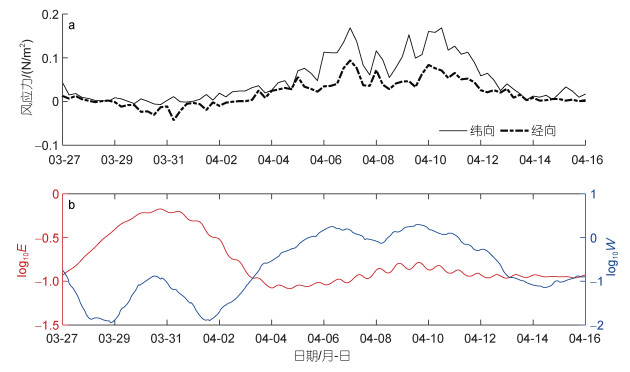 |
| 图 6 T2期间风应力、风生混合层内近惯性能量与近惯性动能 Fig. 6 Wind stress, wind generated near inertial energy flux in mixed layer and near inertial kinetic energy during T2 注: a: 风应力时间序列; b: 风生混合层内近惯性能量通量(W, 单位: J/m3; 蓝线)和近惯性动能(E, 单位: mW/m2; 红线) |
双相干谱是分析三波间非线性相互作用常用的分析方法(Carter et al, 2006; Xie et al, 2011, 2013; Ansong et al, 2018), 当双相干值超出置信水平时, 三波间则为可信的非线性耦合。图 7a是T1期间的双相干值, 结果显示f、D2-f和D2三波间的双相干值在约130~250 m深度上超出80%的置信水平, 尤其是从约200 m深度附近, 超出95%置信水平, 双相干值接近于1, 表明该深度范围内出现显著的f、D2-f和D2三波共振, 能量从D2向f和D2-f传递。另外, 在约330 m、约390 m附近f、D2-f和D2三波间也存在超出90%置信水平的双相干值。图 7a也给出了T1期间D1、D1和D2三波间的双相干值, 发生三波间显著相干的深度与f、D2-f和D2三波间是一致的, 表明南海140.01°E, 18.45°N位置的半日内潮PSI过程不仅有D1的生成, 同时也会生成近惯性波f。除此之外, 图 7a也给出f、D1-f和D1三波间的双相干值。由于全日内潮K1(太阴-太阳赤纬全日分潮)和O1 (太阴赤纬全日分潮)发生PSI过程的临界纬度分别在14.48°N和13.40°N, 而潜标位于临界纬度以外的约400 km处, 很难再发生全日内潮的PSI过程。因此f、D1-f和D1三波间的双相干值是显著低于置信水平的, 几乎接近于0, 该结果也验证了双相干分析方法的正确性。
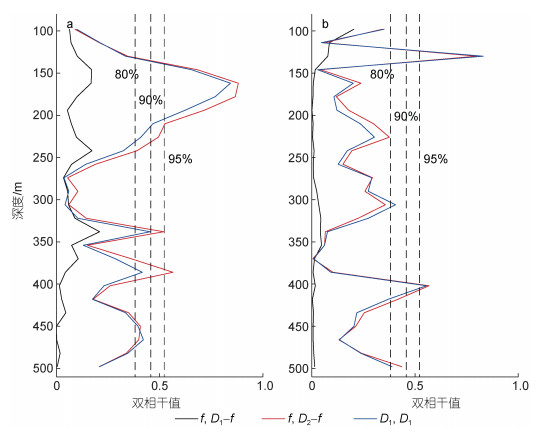 |
| 图 7 双相干值 Fig. 7 Bicoherence value 注: a: T1期间双相干值; b: T2期间双相干值; 虚线表示80%、90%和95%的置信水平 |
图 7b是T2期间的双相干值。总体上该时段内双相干值的深度分布与T1期间的结果相类似。首先, f、D2-f和D2三波与D1、D1和D2三波间在约130 m和约400 m都出现了显著的双相干值, 表明这些深度附近出现显著的三波共振, 半日内潮能量向D1、f和D2-f频转移。其次, f、D2-f和D2与D1、D1和D2的双相干值在深度分布上是相一致的, 表明半日内潮向D1转移能量的期间, 也同时出现能量向f和D2-f转移。但注意到T2时段内发生超出80%置信水平的三波共振大约只有20~30 m的厚度(125~145 m; 400~430 m), 而T1时段内发生超出80%置信水平的三波共振可以超出100 m的厚度(140~250 m)。这可能是由于T2期间的半日内潮幅值弱于T1期间半日内潮的幅值, 从而发生显著的PSI过程就更加困难(MacKinnon et al, 2013; Ansong et al, 2018)。
波数频率谱可以刻画不同频率不同尺度的能量分布和传播特性(Wang et al, 2021), 当垂直波数大于0时表示能量下传, 反之表示能量上传。所以黑线以上部分表示下传能量在波数频率上的分布, 黑线以下部分表示上传能量在波数频率上的分布。波数频率谱显示内波谱段上能量显著的频率分别出现在f、D1和D2 (图 8)。一般而言, 在能量传播方向上, D1、D2上传与下传能量占比相当, f能量在上层海洋则以风生下传为主。然而结果显示f的上传能量相对下传能量是相当的, 表明一定存在非风生过程生成的f频能量。另外, 显著的能量也出现在D2-f频率上, 即使该部分能量相对f、D1和D2较弱, 但由于其具有较大的垂直波数(或者是较小的垂直尺度约0.007 cpm), 所以该频率的能量对促发能量破碎与混合过程是重要的。通过波数频率谱表明观测时段上内波谱除具有普遍存在的f、D1和D2运动外, 同样出现小尺度的D2-f运动和能量上传特征的f运动, 因此, 这些特征进一步证实存在D2通过PSI过程生成f和D2-f运动。
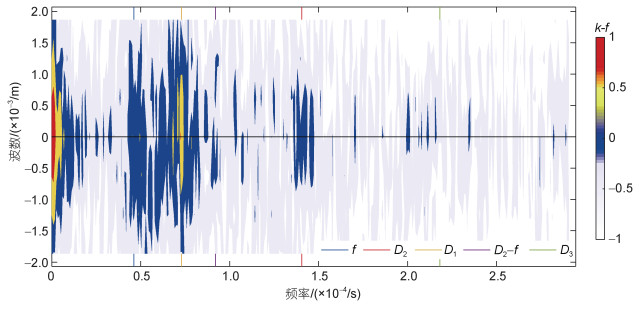 |
| 图 8 波数频率谱 Fig. 8 Vertical wave number-frequency spectrum 注: 颜色表示取10为底对数之后的波数频率谱, 单位m3/s3; f、M2、D1、D2-f、D3分别表示惯性、半日、全日、半日减惯性和三分之一日频率 |
模式研究表明, 半日内潮PSI过程显著发生的区域主要位于25°~30°N (MacKinnon et al, 2005; Ansong et al, 2018)。但Xie等(2011, 2021)在20.58°N陆坡区发现由于低模态半日内潮在表层反射后与入射的半日内潮叠加会增强不稳定的发生, 从而增强PSI过程。图 9给出2021年2月13~18日半日内潮顺时针和逆时针旋转分量, 结果显示半日内潮具有明显的下传和上传特征, 而此时f和D2-f动能都具有增强的特征(图 3b和图 3d)。因此显著的PSI过程可能是由于陆坡区的半日内潮在海表反射后与入射的半日内潮叠加, 促进半日内潮的不稳定性, 从而增强PSI的发生。
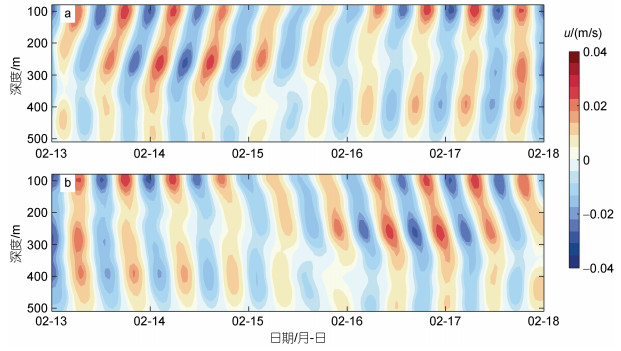 |
| 图 9 半日内潮速度顺时针和逆时针旋转分量 Fig. 9 Clockwise-rotary and anticlockwise-rotary semidiurnal velocity 注: a: 半日潮顺时针旋转速度分量; b: 半日潮逆时针旋转速度分量 |
以往研究很少有定量地计算半日内潮PSI过程下混合的时间变化。本文的潜标观测不仅有流速剖面还有温盐剖面数据, 因此GHP细尺度参数化方法可以应用于海洋混合的估算。需要注意的是, 由于GHP方法是基于波数谱积分估算混合, 以往研究通常取320 m长的剖面计算波数谱(Kunze et al, 2006), 本文中选择的剪切和层结剖面范围为106~426 m。另外, 本文只比较T1期间与T1之后一个月的混合, 一方面是因为T1时段内发生PSI过程的深度较厚, 可以超过100 m的厚度, 而T2期间发生PSI过程厚度较薄, 只有不到30 m, 这时再用GHP细尺度参数化方法会很大程度低估T2期间PSI过程引起的混合; 另一反面是T1时段内发生PSI过程的深度更深, 位于150 m以深, 而T2期间发生的PSI过程较浅, 主要在150 m以浅, 所以GHP参数化方法同样也会低估T2期间PSI过程引起的混合。
图 10a和图 10b分别是流速垂向剪切方与浮力频率方, 结果显示T1期间剪切增强, 尤其是在2月13日的约200~500 m深度上, 剪切增强显著。图 10c和图 10d是湍动能耗散率和扩散率, 其平均值分别是εmean=3.6×10-10 W/kg, κmean=1.8×10-6 m2/s。湍动能耗散率和扩散率的最大值出现在T1期间的2月13日, 分别是εmax=1.3×10-9 W/kg, κmax=6.3×10-6 m2/s, 是平均值的3.6倍和3.5倍。2月11~18日湍动能耗散率和扩散率要高出平均值, 该期间内的平均湍动能耗散率和扩散率分别是7.5×10-10 W/kg和3.2×10-6 m2/s, 是平均结果的2.1和1.8倍。综上可得, 由于T1期间发生显著的PSI过程, 湍动能耗散率和扩散率在该时期内出现增强, 但增强的大小是中等的并没有特别的剧烈。
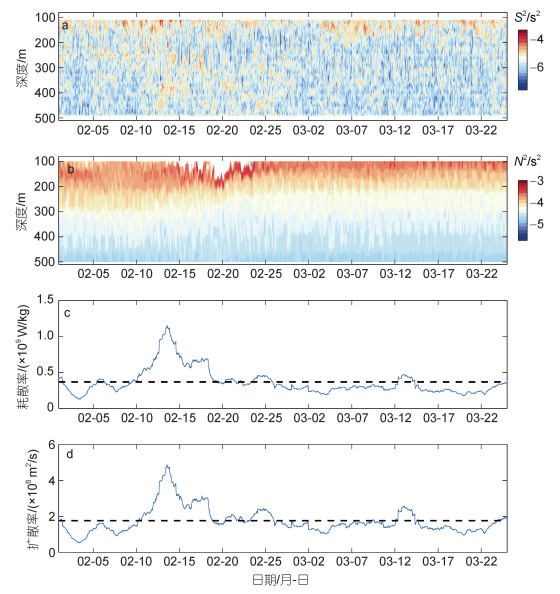 |
| 图 10 GHP细尺度参数化混合估算 Fig. 10 Mixing estimation by GHP fine-scale parameterization 注: a: 流速垂向剪切方; b: 浮力频率方; c: 湍动能耗散率; d: 扩密度扩散率; c和d中的水平虚线是该时间段内的平均值; S2和N2分别表示剪切方和层结 |
参量次谐频不稳定是低模态内潮向高模态内波传递能量的一种重要机制, 可以将能量正向串级至小尺度, 从而促进内波的破碎, 为海洋混合提供能量。因此研究内潮的参量次谐频不稳定过程对于认识混合的空间分布具有重要的意义。本文基于国家重点研发项目的准实时传输深海潜标资料, 主要研究南海西北部陆坡区非临界纬度上半日内潮PSI过程生成的NIW并通过GHP参数化方法给出混合的时间分布特征。主要得到以下结论:
(1) 通过平板模型和双相干谱分析表明, 潜标观测到的上层海洋非风生近惯性能量主要是来自于半日内潮的PSI过程。
(2) 内波速度谱结果显示在发生显著PSI过程的深度上, 生成的近惯性能量与全日频能量相当, D2-f能量与半日频能量相当, 表明PSI生成的惯性能量和D2-f能量与内潮能量是同等重要的。
(3) 虽然模式表明半日内潮PSI显著区域是位于25-30°N (MacKinnon et al, 2005; Ansong et al, 2018), 但在南海西北部陆坡区18.45°N同样观测到半日内潮的PSI过程。该位置, PSI过程不仅有D1运动的生成, 同时也会有f和D2-f运动的生成。这可能是由于南海西北陆坡区的半日内潮在海表反射后与入射的半日内潮叠加, 促进半日内潮的不稳定性, 从而增强PSI的发生(Xie et al, 2011, 2016, 2021)。
(4) 强半日内潮运动期间会有更显著的PSI过程, 半日内潮运动具有低模态的特征, 而半日内潮PSI过程生成的近惯性和D2-f运动具有较高模态。
(5) 通过GHP方法计算半日内潮PSI过程下混合的时间变化, 表明PSI过程下的湍动能耗散率和扩散率在该时期内出现增强。虽然混合的增强是中等的, 但混合中等强度的改变也可能会对海洋模式的结果产生重要的影响(Melet et al, 2013)。
致谢 项目数据来源于国家重点研发计划项目的实时传输潜标任务, 该任务于2020年5月搭载自然资源部东海分局的“向阳红19”号科考船进行了10 d的中期海试验证工作, 特此感谢航次首席李岩刚主任以及全体向阳红19号船队员的全体支持, 该航次验证了整个任务的可靠性和可实施性。在以上工作的基础上, 于2020年11月搭载向阳红14科考船进行最终海试, 并于2021年5月搭载海洋地质4号成功回收, 感谢全部体科考队员为潜标的顺利布放与成功回收所付出的工作。
陈子飞, 于非, 王建丰, 等. 2021. 吕宋海峡不同湍流估算方法的应用对比研究. 海洋与湖沼, 52(1): 27-38 |
管守德, 2014. 南海北部近惯性振荡研究[D]. 青岛: 中国海洋大学博士学位论文.
|
ALFORD M H, 2003. Improved global maps and 54-year history of wind-work on ocean inertial motions. Geophysical Research Letters, 30(8): 1426-1430 |
ALFORD M H, CRONIN M F, KLYMAK J M, 2012. Annual cycle and depth penetration of wind-generated near-inertial internal waves at ocean station papa in the Northeast Pacific. Journal of Physical Oceanography, 42(6): 889-909 DOI:10.1175/JPO-D-11-092.1 |
ALFORD M H, GREGG M C, 2001. Near-inertial mixing: modulation of shear, strain and microstructure at low latitude. Journal of Geophysical Research: Oceans, 106(C8): 16947-16968 DOI:10.1029/2000JC000370 |
ALFORD M H, MACKINNON J A, SIMMONS H L et al, 2016. Near-inertial internal gravity waves in the Ocean. Annual Review of Marine Science, 8: 95-123 DOI:10.1146/annurev-marine-010814-015746 |
ANSONG J K, ARBIC B K, SIMMONS H L et al, 2018. Geographical distribution of diurnal and semidiurnal parametric subharmonic instability in a global ocean circulation model. Journal of Physical Oceanography, 48(6): 1409-1431 DOI:10.1175/JPO-D-17-0164.1 |
CARTER G S, GREGG M C, 2006. Persistent near-diurnal internal waves observed above a site of M2 Barotropic-to-Baroclinic conversion. Journal of Physical Oceanography, 36(6): 1136-1147 DOI:10.1175/JPO2884.1 |
DE Lavergne C, FALAHAT S, MADEC G et al, 2019. Toward global maps of internal tide energy sinks. Ocean Modelling, 137: 52-75 DOI:10.1016/j.ocemod.2019.03.010 |
DUDA T F, RAINVILLE L, 2008. Diurnal and semidiurnal internal tide energy flux at a continental slope in the South China Sea. Journal of Geophysical Research: Oceans, 113(C3): C03025 |
EGBERT G D, RAY R D, 2000. Significant dissipation of tidal energy in the deep ocean inferred from satellite altimeter data. Nature, 405(6788): 775-778 DOI:10.1038/35015531 |
ELGAR S, GUZA R T, 1988. Statistics of bicoherence. IEEE Transactions on Acoustics Speech and Signal Processing, 36(10): 1667-1668 DOI:10.1109/29.7555 |
GARRETT C, MUNK W, 1972. Space-time scales of internal waves. Geophysical Fluid Dynamics, 3(3): 225-264 DOI:10.1080/03091927208236082 |
GREGG M C, 1989. Scaling turbulent dissipation in the thermocline. Journal of Geophysical Research: Oceans, 94(C7): 9686-9698 DOI:10.1029/JC094iC07p09686 |
HENYEY F S, WRIGHT J, FLATTé S M, 1986. Energy and action flow through the internal wave field: an eikonal approach. Journal of Geophysical Research: Oceans, 91(C7): 8487-8495 DOI:10.1029/JC091iC07p08487 |
KELLY S M, JONES N L, NASH J D et al, 2013. The geography of semidiurnal mode-1 internal- tide energy loss. Geophysical Research Letters, 40(17): 4689-4693 DOI:10.1002/grl.50872 |
KIM Y C, POWERS E J, 1979. Digital bispectral analysis and its applications to nonlinear wave interactions. IEEE Transactions on Plasma Science, 7(2): 120-131 DOI:10.1109/TPS.1979.4317207 |
KOROBOV A S, LAMB K G, 2008. Interharmonics in internal gravity waves generated by tide-topography interaction. Journal of Fluid Mechanics, 611: 61-95 DOI:10.1017/S0022112008002449 |
KUNZE E, FIRING E, HUMMON J M et al, 2006. Global abyssal mixing inferred from lowered ADCP shear and CTD strain profiles. Journal of Physical Oceanography, 36(8): 1553-1576 DOI:10.1175/JPO2926.1 |
MACKINNON J A, ALFORD M H, SUN O et al, 2013. Parametric subharmonic instability of the internal tide at 29°N. Journal of Physical Oceanography, 43(1): 17-28 DOI:10.1175/JPO-D-11-0108.1 |
MACKINNON J A, WINTERS K B, 2005. Subtropical catastrophe: Significant loss of low-mode tidal energy at 28.9°N. Geophysical Research Letters, 32(15): L15605 DOI:10.1029/2005GL023376 |
MELET A, HALLBERG R, LEGG S et al, 2013. Sensitivity of the ocean state to the vertical distribution of internal-tide-driven mixing. Journal of Physical Oceanography, 43(3): 602-615 DOI:10.1175/JPO-D-12-055.1 |
MUNK W, WUNSCH C, 1998. Abyssal recipes Ⅱ: Energetics of tidal and wind mixing. Deep Sea Research Part Ⅰ: Oceanographic Research Papers, 45(12): 1977-2010 DOI:10.1016/S0967-0637(98)00070-3 |
MüLler P, HOLLOWAY G, HENYEY F et al, 1986. Nonlinear-Interaction among internal gravity-waves. Reviews of Geophysics, 24(3): 493-536 DOI:10.1029/RG024i003p00493 |
NYCANDER J, 2005. Generation of internal waves in the deep ocean by tides. Journal of Geophysical Research: Oceans, 110(C10): C10028 DOI:10.1029/2004JC002487 |
ONUKI Y, HIBIYA T, 2018. Decay rates of internal tides estimated by an improved wave–wave interaction analysis. Journal of Physical Oceanography, 48(11): 2689-2701 DOI:10.1175/JPO-D-17-0278.1 |
OSBORN T R, 1980. Estimates of the local rate of vertical diffusion from dissipation measurements. Journal of Physical Oceanography, 10(1): 83-89 DOI:10.1175/1520-0485(1980)010<0083:EOTLRO>2.0.CO;2 |
POLLARD R T, MILLARD JR R C, 1970. Comparison between observed and simulated wind-generated inertial oscillations. Deep Sea Research and Oceanographic Abstracts, 17(4): 813-821 DOI:10.1016/0011-7471(70)90043-4 |
POLZIN K L, TOOLE J M, SCHMITT R W, 1995. Finescale parameterizations of turbulent dissipation. Journal of Physical Oceanography, 25(3): 306-328 DOI:10.1175/1520-0485(1995)025<0306:FPOTD>2.0.CO;2 |
SHEEN K L, BREARLEY J A, GARABATO A C N et al, 2013. Rates and mechanisms of turbulent dissipation and mixing in the Southern Ocean: Results from the Diapycnal and Isopycnal Mixing Experiment in the Southern Ocean (DIMES). Journal of Geophysical Research: Oceans, 118(6): 2774-2792 DOI:10.1002/jgrc.20217 |
SHEEN K L, BREARLEY J A, GARABATO A C N et al, 2015. Modification of turbulent dissipation rates by a deep Southern Ocean eddy. Geophysical Research Letters, 42(9): 3450-3457 DOI:10.1002/2015GL063216 |
VIC C, GARABATO A C N, GREEN J A M et al, 2019. Deep-ocean mixing driven by small-scale internal tides. Nature Communications, 10: 2099 DOI:10.1038/s41467-019-10149-5 |
WANG S Y, CAO A Z, CHEN X et al, 2021. On the resonant triad interaction over mid-ocean ridges. Ocean Modelling, 158: 101734 DOI:10.1016/j.ocemod.2020.101734 |
WATERHOUSE A F, MACKINNON J A, NASH J D et al, 2014. Global patterns of diapycnal mixing from measurements of the turbulent dissipation rate. Journal of Physical Oceanography, 44(7): 1854-1872 DOI:10.1175/JPO-D-13-0104.1 |
WHALEN C B, DE LAVERGNE C, GARABATO A C N et al, 2020. Internal Wave-driven mixing: governing processes and consequences for climate. Nature Reviews Earth & Environment, 1(11): 606-621 |
XIE X H, CHEN D K, 2021. Near-surface reflection and nonlinear effects of low-mode internal tides on a continental slope. Journal of Physical Oceanography, 51(4): 1037-1051 DOI:10.1175/JPO-D-20-0197.1 |
XIE X H, LIU Q, SHANG X D et al, 2016. Poleward propagation of parametric subharmonic instability-induced inertial waves. Journal of Geophysical Research: Oceans, 121(3): 1881-1895 DOI:10.1002/2015JC011194 |
XIE X H, SHANG X D, VAN Haren H et al, 2011. Observations of parametric subharmonic instability-induced near-inertial waves equatorward of the critical diurnal latitude. Geophysical Research Letters, 38(5): L05603 |
XIE X H, SHANG X D, VAN Haren H et al, 2013. Observations of enhanced nonlinear instability in the surface reflection of internal tides. Geophysical Research Letters, 40(8): 1580-1586 DOI:10.1002/grl.50322 |
 2022, Vol. 53
2022, Vol. 53


