中国海洋湖沼学会主办。
文章信息
- 马玉祥, 艾丛芳, 董国海. 2022.
- MA Yu-Xiang, AI Cong-Fang, DONG Guo-Hai. 2022.
- 非静压水波模型研究综述
- A REVIEW ON NON-HYDROSTATIC WATER WAVE MODELS
- 海洋与湖沼, 53(4): 813-821
- Oceanologia et Limnologia Sinica, 53(4): 813-821.
- http://dx.doi.org/10.11693/hyhz20220200041
文章历史
-
收稿日期:2022-02-28
收修改稿日期:2022-03-23
诸多的水波模型都是基于一定的假设条件下由Navier-Stokes方程简化而来, 它们都有各自的应用范围。例如, 对Navier-Stokes方程沿水深积分平均, 在一定的假设条件下, 可以推导出二维浅水方程。二维浅水方程适用于水平尺度远大于垂向尺度, 表面波波长大于水深的水流问题(包括河道洪水演进、湖泊环流、海洋潮汐、风暴潮等)的模拟。对于洪水演进这样的水流问题, 二维浅水方程甚至一维浅水方程(即圣维南方程)的计算结果完全可以满足工程上的需要。然而, 自然界中存在的水流运动都是三维的, 一、二维的模型无法得到水平速度沿水深的变化, 因此, 不能模拟水流和输运物质在垂向的升降运动。早期由于计算机计算能力的制约, 广泛应用的三维模型是基于Navier-Stokes方程引入静压假设得到的三维浅水模型。由于三维浅水方程便于数值离散求解、计算量小等优点, 已被广泛应用于天然河道、湖泊、河口, 海岸及近岸水流的模拟中(Casulli et al, 1992; Li et al, 1998; Miglio et al, 1999; 刘桦等, 2000; 赖锡军等, 2006; Xing et al, 2012)。然而, 在水平尺度相对垂向尺度较小的表面波问题以及潮汐与海底山脊相互作用引起的内波问题中, 静压假设已不合理, 这时需要采用考虑到非静压效应的数学模型来求解这些问题。
考虑到非静压效应的数学模型有很多, 包括Boussinesq方程(Mohapatra et al, 2004; Mignot et al, 2009; Kim et al, 2011; Chang et al, 2014; Cantero-Chinchilla et al, 2016; 林鹏程等, 2021; 饶永红等, 2021; 吴亚楠等, 2021)和势流理论(Ma et al, 2001a, 2001b; Hu et al, 2002; Wang et al, 2010)等。Boussinesq方程考虑到了水平和垂直流速沿水深的变化, 通过方程中的频散项来考虑非静压效应的影响。相对于上面提到的浅水方程, Boussinesq方程被广泛地应用于近岸波浪传播演化的模拟。在MIKE 21和SMS等商业软件中均包含了基于Boussinesq方程开发的水波模型。在不可压缩流动的条件下, 假设流动是无旋的, 速度势便满足拉普拉斯方程, 即可应用势流理论来求解涉及非静压效应的水波问题。基于势流理论的数值模型关键是求解速度势满足的拉普拉斯方程。速度势包含了非静压效应的影响, 求解拉普拉斯方程得到速度势之后, 通过速度势与流场的关系就可以直接计算出流场。与基于Euler方程或Navier-Stokes方程的数值模型相比, 基于势流理论的数值模型求解的拉普拉斯方程与压力Poisson方程类似, 在数学上都属于椭圆型方程。然而, 基于势流理论的数值模型无需求解动量方程来计算流场, 这是由流动无旋假设导致的, 也是基于势流理论的数值模型与基于Euler方程或Navier-Stokes方程的数值模型之间的最大区别。
从广义上来讲, 凡是已考虑到非静压效应的数学模型, 并具备模拟频散影响的数值模型皆可称之为非静压模型。从狭义上来讲, 以Euler方程或Navier-Stokes方程作为控制方程, 采用水位函数法计算自由表面的运动的数值模型才称之为非静压模型(Lin et al, 2002; Stelling et al, 2003; Yuan et al, 2004; Bradford, 2005; Zijlema et al, 2005; Anthonio et al, 2006; Wu et al, 2010; Young et al, 2010; Ai et al, 2011, 2019a; Ma et al, 2012)。本文综述的非静压水波模型即为狭义上来说的非静压模型(Kirby, 2017)。狭义上所谓的“非静压模型”是相对浅水模型而来的。在浅水模型中, 只包括了静水压强的影响, 而非静压模型中, 通常把压力项分解为静压项和非静压项之和。相对于浅水模型, 非静压模型刚好多了非静压项, 此即“非静压模型”的名称由来。值得注意的是, 非静压模型的频散效应与非静压项直接相关, 非静压项的求解是非静压模型最为耗时和关键的一步。
1 非静压模型在波浪运动模拟方面的进展非静压模型从20世纪末诞生之日起即被广泛地应用于模拟波浪运动。非静压模型的开发需要解决的一个关键问题是如何准确施加“零压力自由表面边界条件”。Casulli(1999)较早地将三维浅水模型(Casulli et al, 1992)扩展, 建立了三维非静压自由表面流动模型。然而, 此类非静压模型并不是“完全”非静压的模型, 它将自由表面的零压力边界条件直接施加在整个表层上, 即所谓的“表层静压假设”, 从而简化了基于标准交错网格非静压模型的离散求解, 构造了对称正定的压力Poisson方程, 提高了非静压模型的求解效率。这类基于“表层静压假设”构建的非静压模型(Casulli, 1999; Casulli et al, 2002)虽然具有较高的计算效率, 但模拟波浪运动需要增加垂向分层数来提高模型的计算精度。尽管如此, 在波浪传播几个周期之后仍会产生明显的相位误差, 而且波高也会有明显的衰减。
在Casulli的工作之后, 精确施加“零压力自由表面边界条件”, 构建“完全”非静压的自由表面流动数值模型是众多研究者追求的目标(Stelling et al, 2003; Yuan et al, 2004; Zijlema et al, 2005; Anthonio et al, 2006; Cea et al, 2009; Wu et al, 2010; Young et al, 2010; Ai et al, 2011, 2019a; Ma et al, 2012), 其中, 以Stelling等(2003)、Yuan等(2004)、Zijlema等(2005)、Wu等(2010)、Young等(2010)、Ai等(2011)和Ma等(2012)、Ai等(2019a)的工作最具代表性。Stelling等(2003)引入了Keller-box格式, 将非静压项定义在分层网格界面上, 保证了零压力边界条件的精确施加, 首先建立了模拟波浪运动的完全非静压模型。开源的SWASH (Simulating WAves till Shore)非静压模型(Zijlema et al, 2011)即基于Keller-box格式建立的。在Keller-box格式中, 垂向速度与非静压项均定义在分层网格界面上, 这导致了垂向动量方程的离散复杂化, 增加垂向分层数会导致模型难以高效求解, 这限制了该模型只能应用于近岸等浅水条件下波浪传播演化的模拟。Ma等(2012)同样将非静压项定义在分层网格界面上以保证“零压力自由表面边界条件”的准确施加, 但水平速度和垂向速度均定义在分层网格的中心。开源的NHWAVE模型(Non Hydrostatic WAVE model)即为采用这样的变量定义方式实现的非静压模型。NHWAVE需要采用5个垂向分层才能准确模拟(误差小于1%)kh=π的线性色散关系(Ma et al, 2012)。Yuan等(2004)、Wu等(2010)和Young等(2010)基于标准的交错网格, 通过表层垂向积分动量方程确保了在自由表面处压力边界条件的精确给出, 也建立了模拟波浪运动的“完全”非静压模型。上述的“完全”非静压模型, 最终求解的压力Poisson方程均是非对称的, 相对具有对称性的压力Poisson方程而言, 计算较为耗时。
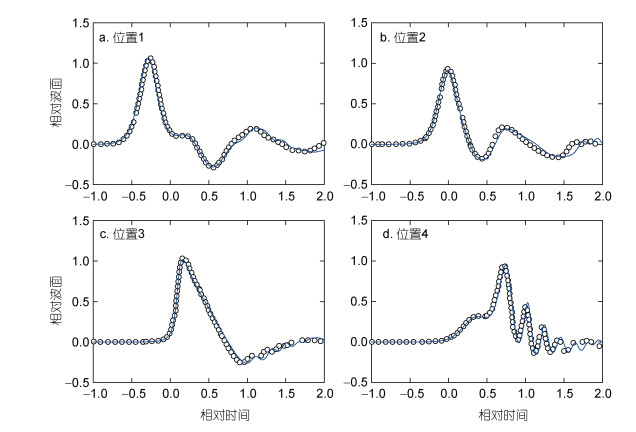
Ai等(2011)和Ai等(2019a)开发的非静压表面流模型抛弃了传统的交错定义变量的方式, 将垂向流速由分层网格界面移到分层网格中心定义, 同时水平流速的仍然按照交错的方式定义(图 1), 同样构建了模拟波浪运动的“完全”非静压模型。相对于其他模型而言(Stelling et al, 2003; Yuan et al, 2004; Zijlema et al, 2005; Anthonio et al, 2006; Cea et al, 2009; Wu et al, 2010; Young et al, 2010; Ma et al, 2012), 采用这种变量定义方式构建的非静压模型的最大特点是最终求解的压力Possion方程是对称正定的, 可以采用预条件共轭梯度法高效求解, 这样极大地提高了非静压模型的计算效率。Ai等(2011)基于垂向边界拟合坐标系统建立了模拟波浪运动的非静压模型(Ai et al, 2011)。该模型采用投影法, 即压力修正法, 求解不可压缩Euler方程。在水平笛卡尔网格框架和垂向边界拟合坐标系下, 提出了上述这种新颖的网格变量定义方式。通过与解析解和试验数据对比, 表明此非静压模型采用两个垂向分层就能够准确高效地模拟波浪浅化、非线性、色散、折射和绕射现象。对于线性色散关系的模拟, 采用两个垂向分层即能准确模拟(误差小于1%) kh=π的深水波浪(图 2)。为实现近岸波浪破碎爬高和强非线性波群的准确模拟, Ai等(2012)对模型进行了扩展, 采用动量守恒的计算格式离散动量方程中的水平对流项, 这使得模型能够有效地模拟包括破碎波和水跃在内的间断流动问题。同时, 再引入干湿动边界处理方法即实现了模型模拟波浪爬高的能力。数值模拟结果表明(图 3), 这样构建的非静压模型可以有效准确地模拟近岸水深变化导致的波浪破碎和爬高过程。为降低非静压模型在模拟强非线性波群时由于压力梯度项离散导致的数值误差, 保证了非静压模型可以准确地模拟强非线性波群的演化, Ai等(2014)首次在非静压模型中引入了广义垂向边界拟合坐标系统。数值模拟结果表明(Ai et al, 2014), 基于广义垂向边界拟合坐标系统建立的非静压模型可以准确地模拟畸形波浪的产生(图 4)。最近, Ai等(2019a)提出了两种半隐的非静压模型来模拟波浪运动。这两种半隐模型同样采用上述变量定义方式构建, 一种是非迭代模型, 另一种需要迭代求解。这类半隐的非静压模型与之前的模型相对比, 具有时间步长不受制于表面波波速的优点, 在模拟深水波浪问题方面更具优势。研究评估和讨论了这两个半隐模型求解线性色散关系的精度和执行效率。通过从浅水到深水的多个数值算例对这两个模型进行了验证。验证结果表明(Ai et al, 2019a), 这两个半隐模型的结果非常相似, 均与实验数据吻合良好(图 5)。然而, 迭代模型的执行效率低于非迭代模型, 求解迭代模型花费的时间是非迭代模型的1.1~2.5倍。
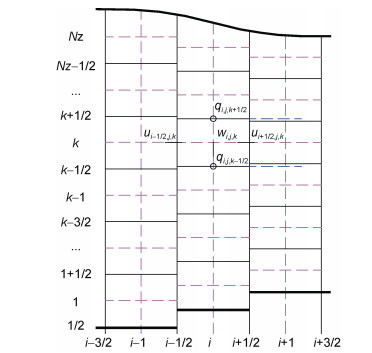 |
| 图 1 非静压模型新颖的变量定义方式(Ai et al, 2011) Fig. 1 Variables definition for the non-hydrostatic model developed by Dalian University of Technology (Ai et al, 2011) 注: i, j, k分别为x, y, z方向的网格索引; u, v分别为水平流速和垂向流速; q为非静压项 |
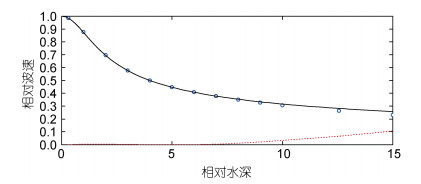 |
| 图 2 线性波波速的计算结果与解析解的对比(Ai et al, 2011) Fig. 2 Comparison of wave celerity between model results and analytical solution (Ai et al, 2011) |
 |
| 图 3 波浪爬高破碎过程(红色实线: 模型结果; 圆点: 实测值)(Ai et al, 2012) Fig. 3 The process of wave runup and breaking (red solid line: model results; dot: experimental data) (Ai et al, 2012) |
 |
| 图 4 畸形波的计算结果与实测数据的对比(红色实线: 模型结果; 圆形: 实测值)(Ai et al, 2014) Fig. 4 Comparison of the freak wave between model results and experimental data (red solid line: model results; circle: experimental data) (Ai et al, 2014) |
 |
| 图 5 聚焦点处三维深水聚焦波的计算结果与实测数据的对比(红色虚线: 非迭代模型结果; 蓝色实线: 迭代模型结果; 圆形: 实测值)(Ai et al, 2019a) Fig. 5 Comparisons of the time histories of the free-surface elevation at the focusing position among the two model results and experimental data (red dash line: non-iterative model results; solid line: iterative model results; circle: experimental data) (Ai et al, 2019a) |
针对模拟强非线性波浪存在沿程波面衰减剧烈, 处理波浪破碎、强间断等问题上性能不足, 压力分裂方法没有及时更新变量信息以及简化的表面应力条件不适用于强非线性波面等问题, Dong等(2019)和He等(2020)提出了三阶中心加权基本无振荡格式(CWENO)和多级黎曼近似解MUSTA的组合方式提高重构精度, 并构建了动压预估校正两步法, 同时完整考虑表面垂向和切向应力, 实现了以较少的垂向分层对深水波浪传播演化(Dong et al, 2019)、深水波浪破碎的准确捕捉和模拟(He et al, 2020)。
波浪在孔隙介质的传播以及与孔隙结构的相互作用涉及非常复杂的多尺度流动耦合, 针对孔隙介质大小形状不一, 内部湍流运动复杂, 传统摩擦阻力系数难以率定以及实尺度、大范围模拟计算成本高等问题, He等(2022)提出了将体积平均的雷诺时均方程与非静压模型相结合的方式, 对体积平均后的k-epsilon湍流模型进行封闭, 统一了孔隙介质内外流动的控制方程, 实现了波浪在包含孔隙结构地形上传播演化的高效准确模拟。
2 非静压模型在波浪-结构物相互作用模拟方面的进展在实际工程中, 常见的各类海洋结构物尤其是目前发展较快的深水海洋结构物当中, 圆柱结构十分常见, 如为海上船舶运输服务的各类透空式码头下部结构中、利用海上风能发电的各类固定式海上风机下部结构中都会见到圆柱结构。波浪与直立圆柱的相互作用问题一直是海岸和海洋工程界关注的问题。在波浪与直立圆柱相互作用的过程中, 波浪的爬高和冲击力可能会对圆柱造成严重的破坏, 因此诸如直立圆柱式海洋结构物的设计必须考虑波浪的作用。目前, 研究者开发了许多数值模型来研究波浪与直立圆柱的相互作用(Li et al, 1999, 2001; Zhao et al, 2007; Zhong et al, 2009)。大多数非静压模型都是在矩形网格基础上开发的。要实现波浪与直立圆柱或更为复杂外形结构物相互作用的模拟, 应构建适应于复杂边界的非静压数值模型。Choi等(2011)基于水平边界适应的曲线坐标系统建立了模拟波浪与复杂边界相互作用的非静压模型。该模型采用基于高阶积分方法的积分表层动量方程以提高表层非静压项的处理精度。数值模拟结果表明, 模型可以较为准确地模拟椭圆余弦波在直立圆柱上的爬高。此后, Choi等(2012)在上述模型的基础上, 又引入了二阶Adams- Bashforth格式和三阶迎风格式来离散对流项以提高模型的精度。在模拟非线性波浪在直立圆柱上的爬高问题时, 模型计算结果与实验数据和二阶绕射理论结果吻合较好。除了上述两个基于水平边界适应的曲线坐标系统建立的非静压模型具备模拟波浪与复杂边界相互作用的能力之外, 其他基于非结构三角形网格构建的非静压模型同样具备这样的能力(Casulli et al, 2002; Cea et al, 2009)。
 |
| 图 6 三角形与四边形混合网格(Ai et al, 2017) Fig. 6 A hybrid-grid of triangular and rectangular cells (Ai et al, 2017) |
大连理工大学在国内较早地建立了模拟波浪与复杂边界结构物相互作用的非结构网格非静压模型(Ai et al, 2010, 2017)。三维计算网格采用覆盖水平计算域的二维计算网格和垂向分层式的结构化网格构建。水平二维计算网格可以采用三角形网格(Ai et al, 2010)或三角形与四边形相结合的混合网格(Ai et al, 2017)。水平对流项的离散采用Perot格式实现(Perot, 2000)。该非静压模型可以模拟波浪与单直立圆柱或多直立圆柱的相互作用。通过与试验数据对比, 证实了模型可以准确地模拟非线性波浪在直立圆柱周围的爬高现象以及作用在直立圆柱上的波浪力。
除了非静压模型在波浪与直立圆柱相互作用方面的模拟应用, 非静压模型也被应用于波浪与水下结构物或浮式结构物相互作用的模拟。Lin(2006)开发了三维多层σ坐标非静压模型, 以模拟波浪与结构物的相互作用, 该模型克服了之前非静压模型(Lin et al, 2002)无法准确模拟涉及间断水深的问题, 仅采用三个垂向分层, 该模型即可准确地模拟波浪与浮式或水下结构物的相互作用。Kang等(2015)对该多层σ坐标模型进行了扩展, 以模拟涉及曲面问题的波浪与结构物相互作用问题, 并成功地将模型应用于波浪与不同淹没深度的垂直圆柱相互作用的模拟研究。Ma等(2016)同样提出了模拟波浪与结构物相互作用的σ坐标非静压模型。对于波浪与底部固定结构物的相互作用, 模型结果与实验数据之间取得了良好的一致性, 但模型在解决波浪与浮式或水下结构物相互作用方面的能力尚未得到证实。Rijnsdorp等(2016)提出了一个基于SWASH (Zijlema et al, 2011)的非静压数值模型。他们的模型能够预测波浪的非线性演变及其对受约束船舶的影响。然而, 该模型不能直接用于模拟波浪与浮式结构物的相互作用。
近年来, Ai等(2018), Ai等(2019b), Ma等(2019)和Ai等(2022b)在其开发的非静压波浪数值模型的基础上, 通过引入浸入边界法实现了波浪与浮式或水下结构物相互作用的模拟。浸入边界法的引入使得非静压模型实现了基于结构化网格模拟波浪与任意形状结构物相互作用的能力。基于广义垂向边界拟合坐标系统, 分别采用半隐分部算法求解Navier-Stokes方程(Ai et al, 2018)和显式投影法求解Euler方程(Ma et al, 2019), 实现了波浪与浮式或水下任意形状结构物相互作用的立面二维模拟。数值模拟结果表明, 所建立的非静压模型可以准确地模拟出浮式或水下结构物对波浪传播演化的影响(图 7)以及波浪作用下结构物的受力情况(Ai et al, 2018; Ma et al, 2019)。另外, 模型还可以模拟波浪与结构物相互作用过程中旋涡的产生以及结构物附近旋涡的演化过程(图 8)。由于上述两个非静压模型均为立面二维模型, 为实现波浪与三维结构物相互作用的模拟, 对上述模型进行扩展建立了三维非静压模型(Ai et al, 2019b)。这样建立的三维模型, 由于浸入边界法的引入破坏了压力Poisson方程的对称性, 降低了模型的求解效率。为改进模型的执行效率, Ai等(2022b)首次将浸入边界法与全局连续性方程相结合建立了高效的三维非静压模型, 在该模型中全局连续性方程用来替代固液边界处的Newmann边界条件, 避免了浸入边界法对压力Poisson方程的不利影响, 保证了压力Poisson方程对称正定的性质, 有效提高了模型的计算效率。在三维波浪与浮式结构物相互作用的模拟中(图 9), 计算效率最高可提高7.6倍(Ai et al, 2022b)。
 |
| 图 7 受水下结构物影响的波面时间序列的计算结果与实测数据的对比(蓝色实线: 模型结果; 圆形: 实测值)(Ma et al, 2019) Fig. 7 Comparisons of the time histories of free-surface elvations between model results and experimental data (blue solid line: model results; circle: experimental data) (Ma et al, 2019) |
 |
| 图 8 结构物附近的流场 Fig. 8 Flow field around the plate |
 |
| 图 9 波浪与浮式沉箱的相互作用 Fig. 9 Wave interaction with a floating caisson |
非静压水波模型的应用十分广泛, 凡是涉及非静压效应的自由表面流动现象都可采用非静压模型模拟。本文综述了非静压模型概念的提出以及数值开发的难点, 主要介绍了非静压模型在波浪传播演化和波浪与结构物相互作用这两方面的应用进展。本文介绍的非静压模型是基于不可压缩Euler方程或Navier-Stokes方程建立的, 在这类模型中, 压力Poisson方程的求解是不可避免的。压力Poisson方程的性质直接关系整个模型的执行效率。高效的非静压水波模型一直是研究者不懈追求的目标。作者希望本文能引起更多的研究者加入到非静压水波模型的开发应用中, 拓宽非静压模型的应用领域。除了本文综述的内容之外, 非静压模型在内波产生和传播演化(Lai et al, 2010; Ai et al, 2016)、海啸波传播(Oishi et al, 2013)、滑坡涌浪(Ai et al, 2021b)、波动涌潮(Ai et al, 2021a)、溃坝波传播演化(Ai et al, 2022a)等方面均有应用。另外, 为提高非静压模型的执行效率, 也可以采用GPU技术并行求解模型(Ai et al, 2019a)。
刘桦, 何友声, 2000. 河口三维流动数学模型研究进展. 海洋工程, 18(2): 87-93 DOI:10.3969/j.issn.1005-9865.2000.02.016 |
吴亚楠, 武贺, 周庆伟, 等, 2021. 基于Boussinesq波浪模型的港池波浪数值模拟与泊稳分析. 海洋通报, 40(3): 301-308 |
林鹏程, 刘忠波, 刘勇, 2021. 基于Boussinesq数值模型的波浪速度垂向分布模拟研究. 海洋湖沼通报, 43(4): 7-15 |
饶永红, 刘忠波, 梁书秀, 等, 2021. 双层Boussinesq模型非线性波浪模拟研究. 水道港口, 42(5): 614-622 DOI:10.3969/j.issn.1005-8443.2021.05.008 |
赖锡军, 曲卓杰, 周杰, 等, 2006. 非结构网格上的三维浅水流动数值模型. 水科学进展, 17(5): 693-699 DOI:10.3321/j.issn:1001-6791.2006.05.017 |
AI C F, DING W Y, 2016. A 3D unstructured non-hydrostatic ocean model for internal waves. Ocean Dynamics, 66(10): 1253-1270 DOI:10.1007/s10236-016-0980-9 |
AI C F, DING W Y, JIN S, 2014. A general boundary-fitted 3D non-hydrostatic model for nonlinear focusing wave groups. Ocean Engineering, 89: 134-145 DOI:10.1016/j.oceaneng.2014.08.002 |
AI C F, DING W Y, JIN S, 2017. A hybrid-grid 3D model for regular waves interacting with cylinders. Journal of Hydraulic Research, 55(1): 129-134 DOI:10.1080/00221686.2016.1212943 |
AI C F, JIN S, 2010. Non-hydrostatic finite volume model for non-linear waves interacting with structures. Computers & Fluids, 39(10): 2090-2100 |
AI C F, JIN S, 2012. A multi-layer non-hydrostatic model for wave breaking and run-up. Coastal Engineering, 62: 1-8 DOI:10.1016/j.coastaleng.2011.12.012 |
AI C F, JIN S, LV B, 2011. A new fully non-hydrostatic 3D free surface flow model for water wave motions. International Journal for Numerical Methods in Fluids, 66(11): 1354-1370 DOI:10.1002/fld.2317 |
AI C F, MA Y X, DING W Y, et al, 2021a. An efficient three-dimensional non-hydrostatic model for undular bores in open channels. Physics of Fluids, 33(12): 127111 DOI:10.1063/5.0073241 |
AI C F, MA Y X, DING W Y, et al, 2022a. Three-dimensional non-hydrostatic model for dam-break flows. Physics of Fluids, 34(2): 022105 DOI:10.1063/5.0081094 |
AI C F, MA Y X, YUAN C F, et al, 2018. Semi-implicit non-hydrostatic model for 2D nonlinear wave interaction with a floating/suspended structure. European Journal of Mechanics-B/Fluids, 72: 545-560 DOI:10.1016/j.euromechflu.2018.08.003 |
AI C F, MA Y X, YUAN C F, et al, 2019a. Development and assessment of semi-implicit nonhydrostatic models for surface water waves. Ocean Modelling, 144: 101489 DOI:10.1016/j.ocemod.2019.101489 |
AI C F, MA Y X, YUAN C F, et al, 2019b. A 3D non-hydrostatic model for wave interactions with structures using immersed boundary method. Computers & Fluids, 186: 24-37 |
AI C F, MA Y X, YUAN C F, et al, 2021b. A three-dimensional non-hydrostatic model for tsunami waves generated by submarine landslides. Applied Mathematical Modelling, 96: 1-19 DOI:10.1016/j.apm.2021.02.014 |
AI C F, MA Y X, YUAN C F, et al, 2022b. An efficient 3D non-hydrostatic model for predicting nonlinear wave interactions with fixed floating structures. Ocean Engineering, 248: 110810 DOI:10.1016/j.oceaneng.2022.110810 |
ANTHONIO S L, HALL K R, 2006. High-order compact numerical schemes for non-hydrostatic free surface flows. International Journal for Numerical Methods in Fluids, 52(12): 1315-1337 DOI:10.1002/fld.1225 |
BRADFORD S F, 2005. Godunov-based model for nonhydrostatic wave dynamics. Journal of Waterway, Port, Coastal, and Ocean Engineering, 131(5): 226-238 DOI:10.1061/(ASCE)0733-950X(2005)131:5(226) |
CANTERO-CHINCHILLA F N, CASTRO-ORGAZ O, DEY S, et al, 2016. Nonhydrostatic dam break flows. I: physical equations and numerical schemes. Journal of Hydraulic Engineering, 142(12): 04016068 DOI:10.1061/(ASCE)HY.1943-7900.0001205 |
CASULLI V, 1999. A semi-implicit finite difference method for non-hydrostatic, free-surface flows. International Journal for Numerical Methods in Fluids, 30(4): 425-440 DOI:10.1002/(SICI)1097-0363(19990630)30:4<425::AID-FLD847>3.0.CO;2-D |
CASULLI V, CHENG R T, 1992. Semi-implicit finite difference methods for three-dimensional shallow water flow. International Journal for Numerical Methods in Fluids, 15(6): 629-648 DOI:10.1002/fld.1650150602 |
CASULLI V, ZANOLLI P, 2002. Semi-implicit numerical modeling of nonhydrostatic free-surface flows for environmental problems. Mathematical and Computer Modelling, 36(9/10): 1131-1149 |
CEA L, STELLING G, ZIJLEMA M, 2009. Non-hydrostatic 3D free surface layer-structured finite volume model for short wave propagation. International Journal for Numerical Methods in Fluids, 61(4): 382-410 DOI:10.1002/fld.1961 |
CHANG T J, CHANG K H, KAO H M, 2014. A new approach to model weakly nonhydrostatic shallow water flows in open channels with smoothed particle hydrodynamics. Journal of Hydrology, 519: 1010-1019 DOI:10.1016/j.jhydrol.2014.08.030 |
CHOI D Y, WU C H, YOUNG C C, 2011. An efficient curvilinear non-hydrostatic model for simulating surface water waves. International Journal for Numerical Methods in Fluids, 66(9): 1093-1115 DOI:10.1002/fld.2302 |
CHOI D Y, YUAN H L, 2012. A horizontally curvilinear non-hydrostatic model for simulating nonlinear wave motion in curved boundaries. International Journal for Numerical Methods in Fluids, 69(12): 1923-1938 DOI:10.1002/fld.2676 |
DONG G H, FU R L, MA Y X, et al, 2019. Simulation of unidirectional propagating wave trains in deep water using a fully non-hydrostatic model. Ocean Engineering, 180: 254-266 DOI:10.1016/j.oceaneng.2019.03.037 |
HE D B, MA Y X, DONG G H, et al, 2020. Predicting deep water wave breaking with a non-hydrostatic shock-capturing model. Ocean Engineering, 216: 108041 DOI:10.1016/j.oceaneng.2020.108041 |
HE D B, MA Y X, DONG G H, et al, 2022. A numerical investigation of wave and current fields along bathymetry with porous media. Ocean Engineering, 244: 110333 DOI:10.1016/j.oceaneng.2021.110333 |
HU P X, WU G X, MA Q W, 2002. Numerical simulation of nonlinear wave radiation by a moving vertical cylinder. Ocean Engineering, 29(14): 1733-1750 DOI:10.1016/S0029-8018(02)00002-1 |
KANG A Z, LIN P Z, LEE Y J, et al, 2015. Numerical simulation of wave interaction with vertical circular cylinders of different submergences using immersed boundary method. Computers & Fluids, 106: 41-53 |
KIM D H, LYNETT P J, 2011. Dispersive and nonhydrostatic pressure effects at the front of surge. Journal of Hydraulic Engineering, 137(7): 754-765 DOI:10.1061/(ASCE)HY.1943-7900.0000345 |
KIRBY J T, 2017. Recent advances in nearshore wave, circulation, and sediment transport modeling. Journal of Marine Research, 75(3): 263-300 DOI:10.1357/002224017821836824 |
LAI Z G, CHEN C S, COWLES G W, et al, 2010. A nonhydrostatic version of FVCOM: 2. Mechanistic study of tidally generated nonlinear internal waves in Massachusetts Bay. Journal of Geophysical Research, 115(C12): C12049 |
LI Y S, LIU S X, YU Y X, et al, 1999. Numerical modeling of Boussinesq equations by finite element method. Coastal Engineering, 37(2): 97-122 DOI:10.1016/S0378-3839(99)00014-9 |
LI Y S, ZHAN J M, 1998. Three-dimensional finite-element model for stratified coastal seas. Journal of Hydraulic Engineering, 124(7): 699-703 DOI:10.1061/(ASCE)0733-9429(1998)124:7(699) |
LI Y S, ZHAN J M, 2001. Boussinesq-type model with boundary-fitted coordinate system. Journal of Waterway, Port, Coastal, and Ocean Engineering, 127(3): 152-160 DOI:10.1061/(ASCE)0733-950X(2001)127:3(152) |
LIN P Z, 2006. A multiple-layer σ-coordinate model for simulation of wave-structure interaction. Computers & Fluids, 35(2): 147-167 |
LIN P Z, LI C W, 2002. A σ-coordinate three-dimensional numerical model for surface wave propagation. International Journal for Numerical Methods in Fluids, 38(11): 1045-1068 DOI:10.1002/fld.258 |
MA G F, FARAHANI A A, KIRBY J T, et al, 2016. Modeling wave-structure interactions by an immersed boundary method in a σ-coordinate model. Ocean Engineering, 125: 238-247 DOI:10.1016/j.oceaneng.2016.08.027 |
MA G F, SHI F Y, KIRBY J T, 2012. Shock-capturing non-hydrostatic model for fully dispersive surface wave processes. Ocean Modelling, 43/44: 22-35 DOI:10.1016/j.ocemod.2011.12.002 |
MA Q W, WU G X, TAYLOR R E, 2001a. Finite element simulation of fully non-linear interaction between vertical cylinders and steep waves. Part 1: methodology and numerical procedure. International Journal for Numerical Methods in Fluids, 36(3): 265-285 DOI:10.1002/fld.131 |
MA Q W, WU G X, TAYLOR R E, 2001b. Finite element simulations of fully non-linear interaction between vertical cylinders and steep waves. Part 2: numerical results and validation. International Journal for Numerical Methods in Fluids, 36(3): 287-308 DOI:10.1002/fld.133 |
MA Y X, YUAN C F, AI C F, et al, 2019. Comparison between a non-hydrostatic model and OpenFOAM for 2D wave-structure interactions. Ocean Engineering, 183: 419-425 DOI:10.1016/j.oceaneng.2019.05.002 |
MIGLIO E, QUARTERONI A, SALERI F, 1999. Finite element approximation of quasi-3D shallow water equations. Computer Methods in Applied Mechanics and Engineering, 174(3/4): 355-369 |
MIGNOT E, CIENFUEGOS R, 2009. On the application of a Boussinesq model to river flows including shocks. Coastal Engineering, 56(1): 23-31 DOI:10.1016/j.coastaleng.2008.06.007 |
MOHAPATRA P K, CHAUDHRY M H, 2004. Numerical solution of Boussinesq equations to simulate dam-break flows. Journal of Hydraulic Engineering, 130(2): 156-159 DOI:10.1061/(ASCE)0733-9429(2004)130:2(156) |
OISHI Y, PIGGOTT M D, MAEDA T, et al, 2013. Three-dimensional tsunami propagation simulations using an unstructured mesh finite element model. Journal of Geophysical Research: Solid Earth, 118(6): 2998-3018 DOI:10.1002/jgrb.50225 |
PEROT B, 2000. Conservation properties of unstructured staggered mesh schemes. Journal of Computational Physics, 159(1): 58-89 DOI:10.1006/jcph.2000.6424 |
RIJNSDORP D P, ZIJLEMA M, 2016. Simulating waves and their interactions with a restrained ship using a non-hydrostatic wave-flow model. Coastal Engineering, 114: 119-136 DOI:10.1016/j.coastaleng.2016.04.018 |
STELLING G, ZIJLEMA M, 2003. An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation. International Journal for Numerical Methods in Fluids, 43(1): 1-23 DOI:10.1002/fld.595 |
WANG C Z, WU G X, 2010. Interactions between fully nonlinear water waves and cylinder arrays in a wave tank. Ocean Engineering, 37(4): 400-417 DOI:10.1016/j.oceaneng.2009.12.006 |
WU C H, YOUNG C C, CHEN Q, et al, 2010. Efficient nonhydrostatic modeling of surface waves from deep to shallow water. Journal of Waterway, Port, Coastal, and Ocean Engineering, 136(2): 104-118 DOI:10.1061/(ASCE)WW.1943-5460.0000032 |
XING Y, AI C F, JIN S, 2013. A three-dimensional hydrodynamic and salinity transport model of estuarine circulation with an application to a macrotidal estuary. Applied Ocean Research, 39: 53-71 DOI:10.1016/j.apor.2012.10.003 |
YOUNG C C, WU C H, 2010. Nonhydrostatic modeling of nonlinear deep-water wave groups. Journal of Engineering Mechanics, 136(2): 155-167 DOI:10.1061/(ASCE)EM.1943-7889.0000078 |
YUAN H L, WU C H, 2004. An implicit three-dimensional fully non-hydrostatic model for free-surface flows. International Journal for Numerical Methods in Fluids, 46(7): 709-733 DOI:10.1002/fld.778 |
ZHAO M, CHENG L, TENG B, 2007. Numerical simulation of solitary wave scattering by a circular cylinder array. Ocean Engineering, 34(3/4): 489-499 |
ZHONG Z Y, WANG K H, 2009. Modeling fully nonlinear shallow-water waves and their interactions with cylindrical structures. Computers & Fluids, 38(5): 1018-1025 |
ZIJLEMA M, STELLING G S, 2005. Further experiences with computing non-hydrostatic free-surface flows involving water waves. International Journal for Numerical Methods in Fluids, 48(2): 169-197 DOI:10.1002/fld.821 |
ZIJLEMA M, STELLING G, SMIT P, 2011. SWASH: an operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coastal Engineering, 58(10): 992-1012 DOI:10.1016/j.coastaleng.2011.05.015 |
 2022, Vol. 53
2022, Vol. 53


