中国海洋湖沼学会主办。
文章信息
- 杜文彦, 张旭日, 张丽丽, 尤再进, 石洪源. 2022.
- DU Wen-Yan, ZHANG Xu-Ri, ZHANG Li-Li, YOU Zai-Jin, SHI Hong-Yuan. 2022.
- 基于ERA5再分析数据的中国邻近海域极端波高特征分析
- CHARACTERISTICS OF EXTREME WAVE HEIGHT IN CHINA'S MARGINAL SEAS BASED ON ERA5 REANALYSIS DATA
- 海洋与湖沼, 53(4): 1007-1014
- Oceanologia et Limnologia Sinica, 53(4): 1007-1014.
- http://dx.doi.org/10.11693/hyhz20220100003
文章历史
-
收稿日期:2022-01-03
收修改稿日期:2022-03-10
2. 大连海事大学港口与航运安全协同创新中心 辽宁大连 116000
2. Centre for Ports and Maritime Safety, Dalian Maritime University, Dalian 116000, China
海浪会对海岸结构物、近海泥沙运输、海岸侵蚀等造成影响。因此, 它是沿海灾害的一个重要因素。大浪叠加潮汐将进一步增加沿海地区的脆弱性(Wang et al, 2012)。海浪由风产生, 很多学者已经研究了全球波高的历史变化趋势(Patra et al, 2016; Patra et al, 2017)。此外, 年际气候变化模式如厄尔尼诺-南方涛动(El Niño-Southern Oscillation, ENSO)、北大西洋涛动(North Atlantic Oscillation, NAO)等将造成大气环流的改变, 最终影响整个全球海洋表面的风应力(Dodet et al, 2010)。因此, 气候变化通过影响海洋-大气相互作用、风和台风活动来影响全球波浪的变化(Hemer et al, 2010; Bromirski et al, 2013)。
极端波浪对沿海地区基础设施有着深远的影响, 了解它们的变化规律是进行海岸带风险分析和灾害预防的基础。然而, 关于气候变化对全球范围内极端波浪影响的研究十分有限。众所周知, 气候变化对平均波高具有影响, 但由于短时间尺度的相关分析噪声较大, 它们对极端波浪的影响尚未被深刻认识。此外, 由于极端波浪的非正态性, 简单线性回归分析不能应用于其研究。因此, 学者们开始使用极端函数理论研究气候变化与极端波浪的相关性。Izaguirre等(2011)对卫星高度计数据集的月最大显著波高(significant wave heights, SWH)进行了非平稳广义极值(generalized extreme value, GEV)分析, 将气候变化指数作为GEV位置参数的附加协变量。分析了ENSO、NAO等10种大尺度气候变化对全球年极端波高的影响, 但尚未评估对极端波高的季节贡献。Kumar等(2016)基于欧洲中期天气预报中心再分析数据集ERA-Interim和ERA-20C再分析数据, 利用GEV分析研究了ENSO和PDO对北方冬季(11月到次年2月)期间的极端波高的影响。Kumar等(2019)利用相同的方法及ERA-20C再分析数据, 研究了印度洋上的极端SWH对ENSO、SAM的季节性反应, 发现了同样的物理机制。Patra等(2020)等利用同样的方法及卫星和欧洲中期天气预报中心第五代再分析数据集(ECMWF reanalysis v5, ERA5), 分析了ENSO等10余种气候变化对全球极端波高的影响。
目前, 针对中国近海波浪特征的研究很多, 有的基于实测数据(吴迪茜等, 2021), 有的基于卫星遥感资料(李文博等, 2017)和数值模型(郑崇伟等, 2013), 也有的基于再分析数据(乔守文等, 2020; 邱文博等, 2021), 研究结果指出, 我国海域波浪呈现出明显的季节特征, 其中秋冬季节波高大, 春夏季节波高小。因全球变暖等因素, 厄尔尼诺现象发生频率及影响程度不断增强, 目前有关我国海域极端波高的变化特征研究较少, 更鲜有研究定量指出厄尔尼诺现象与极端波高之间的关联性。因此, 本文采用ERA5数据分析我国极端波高的变化特征, 并利用GEV函数探究厄尔尼诺现象对我国海域极端波高的影响。
1 数据资料 1.1 研究区域中国近海海域包括渤海、黄海、东海和南海以及台湾东侧的太平洋部分海域, 位于北太平洋西部的边缘地区南北跨越44个纬度, 本文研究的中国临近海范围为(7°~41°N, 105.5°~126.5°E)(图 1)。
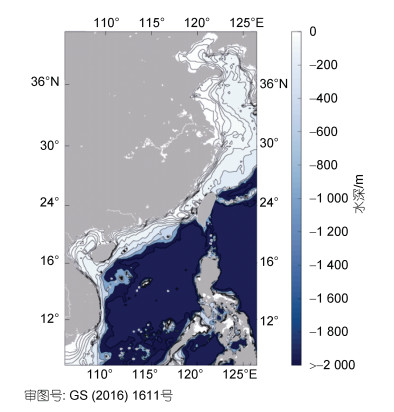 |
| 图 1 研究区域地形水深图 Fig. 1 Topography and bathymetry of the study area |
ECMWF是全球几家最主要的再分析数据中心之一。ERA5是ECMWF第五代再分析数据集。它是欧洲中期天气预报中心最新的再分析产品。ERA5涵盖了1979年到最近的再分析数据, 目前还在不断更新中。相比ERA-Interim, ERA5同化系统使用了若干专为再分析而开发的综合预报系统(integrated forecasting system, IFS cycle 41r2), 数据准确性得到了显著改善。ERA5数据具有高分辨率: 水平分辨率为31 km (~0.25°), 垂向为从地表开始137层。以往ERA数据产品在波浪波高模拟中普遍存在偏低的现象, 而ERA5数据已经有较大的改进(李朝等, 2021), ERA5提供的变量从ERA-Interim的100个增加到240个, 其中包括耦合波浪模型提供的波高和波向, 使用户能够更准确地分析过去的大气和海洋状态。许多研究人员将其用于大气和海洋研究(Stopa et al, 2013)。ERA5在我国的适用性已有学者(Shi et al, 2021)研究, 因此, 本文选择ERA5再分析数据用于本文相关研究。
本文按照世界气象学会的定义, 四季划分标准为: 春季(MAM), 包括3、4和5月; 夏季(JJA), 包括6、7和8月; 秋季(SON), 包括9、10和11月; 冬季(DJF), 包括12、1和2月。
2 研究区域极端波高时空变化特征分析 2.1 极端波高的年特征分析早期的文章对极端波高的定义是, 在总体波高数据中选取一个最大值数据, 但由于台风等极端天气对这种极值的影响极大, 故这种方法可能会提供不可靠的极端样本值的估计。为克服这一缺点, 本文采用了波高大于整体数据阈值的波高均值来定义极端波高, 所选阈值为每个数据点的所有波高数据的第98个百分位(Menéndez et al, 2008)。
2.1.1 极端波高年趋势变化空间分布通过对1979~2018年前2%极端波高统计和推算, 得出极端波高年均图、波高年趋势变化分布图和50年一遇及100年一遇(图 2)。由图 2可见, 渤海及黄海海域的极端波高年均值约在3 m, 东海南部、台湾海峡周边及南海东北部海域极端波高年均值较大, 约在5~6 m。
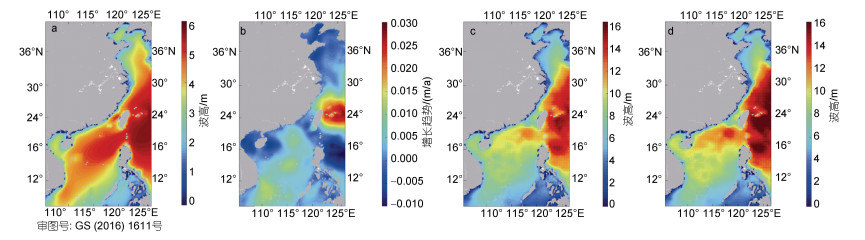 |
| 图 2 1979~2018年极端波高年均值图(a)、极端波高年趋势变化空间分布图(b)、50年一遇极值波高推算图(c)和100年一遇极值波高推算图(d) Fig. 2 Annual averages of extreme wave heights (a), spatial distribution of extreme wave height trend (b), 50-year (c)- and 100-year (d) projection of extreme wave height from 1979 to 2018 |
由图 2可见, 台湾岛东北部地区及东海南部大部分地区极端波高呈明显增长趋势, 增长幅度在0.025 m/a左右, 南海大部分海域也处于增长趋势, 增长幅度基本在0.01 m/a左右浮动, 渤海、黄海大部分海域及海南岛周边海域呈减小趋势, 其削减幅度在0.005 ~0.010 m/a左右。在50年一遇和100年一遇极值波高图中, 渤海和黄海大部分海域的波高在4~6 m, 可以看出波高大值区域集中在东海海域, 南海大部分海域波高在10 m左右, 在东沙群岛和巴士海峡附近波高较大, 在11~14 m左右。
2.1.2 极端波高年际变化分布图 3为1979~2018年间本文研究区域2%极端年均波浪高度的变化情况, 整个区域逐小时的有效波高累加求平均, 可以看出本文研究海域2%极端年均波浪在3~4 m间浮动, 且整体趋势递增, 其中1988年和1996年波高值出现较大波动。
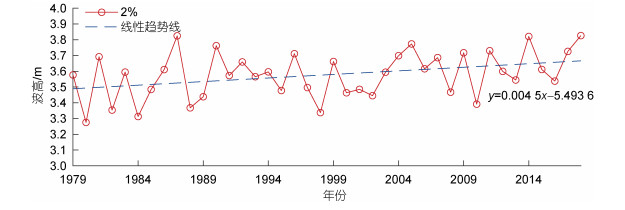 |
| 图 3 1979~2018年极端波高季节变化趋势图 Fig. 3 Seasonal trend of extreme wave height from 1979 to 2018 |
通过对40年季均前2%极端波高统计, 得出极端波高季均分布图及波高季节趋势变化分布图(图 4~5)。由图 4可见, 春季和夏季的季节均值极端波高较秋季和冬季小, 春季大部分海域极端波高在3.5~4 m左右, 台湾海峡西侧极端波高较高在4.5 m左右; 夏季东海东南部极端波高值在5 m以上在四个海域中最为显著; 秋季研究海域较大值集中在东海南部和南海中北部; 冬季整个研究区域极端波高值普遍较高, 大部分海域极端波高在4~4.5 m左右。
 |
| 图 4 1979~2018年极端波高四季均值分布图 Fig. 4 Mean distribution of extreme wave height in four seasons from 1979 to 2018 |
 |
| 图 5 1979~2018年极端波高四季趋势变化空间分布 Fig. 5 Spatial distribution of extreme wave height trend in four seasons from 1979 to 2018 |
1979~2018年极端波高各季节趋势变化分布图显示, 春季渤海及黄海呈下降, 其下降幅度约在0.005 m/a, 太平洋西部地区则为增长趋势, 增长幅度在0.035 m/a左右, 南海大部分地区增长幅度在0.02 m/a; 在夏季和秋季, 南海西南部为下降趋势, 在0.02 m/a左右, 而东海南部及西部则为增长趋势, 夏季在台湾岛东部增长趋势明显, 约在0.04 m/a, 秋季台湾岛东北部及东海中南部增长趋势幅度约为0.03 m/a; 冬季期间, 渤海地区呈现下降趋势, 幅度在0.01 m/a左右浮动, 台湾海峡南侧及西沙群岛周边海域则为明显的上升趋势, 上升幅度在0.025 m/a左右。
2.2.2 极端波高季节变化分布为了体现变化趋势的季节性差异, 本文还分析了近40 a期间研究区域海域逐春季、逐夏季、逐秋季、逐冬季2%极端波浪的变化趋势(图 6)。由图 6可见, 大部分海域的大浪频率表现出显著性递增趋势; 春季波高波动幅度最大, 幅度最显著时能达到1 m, 在1.9~3.5 m之间且整体波高较小, 其中在1991、1996、2005、2006和2011年波动较为明显; 夏季波浪高度波动明显, 极端波高在1.5~3.9 m左右, 其中1987、1988、1998、2010和2015年波动值显著, 最大可达到2 m左右; 夏季和秋季极端波高变化趋势较春季和冬季相对平缓, 秋季极端波高较大在3~4.5 m之间浮动, 其中在1983、1993、2007、2009和2015年出现突变值, 最大波动在1983年出现可达到1.4 m左右; 冬季极端波高变化趋势为上升趋势, 波高在3~4.2 m左右浮动, 在1981、1988、1991、1993和1999年出现明显波动, 在1993年发生波动最显著, 达到0.8 m。
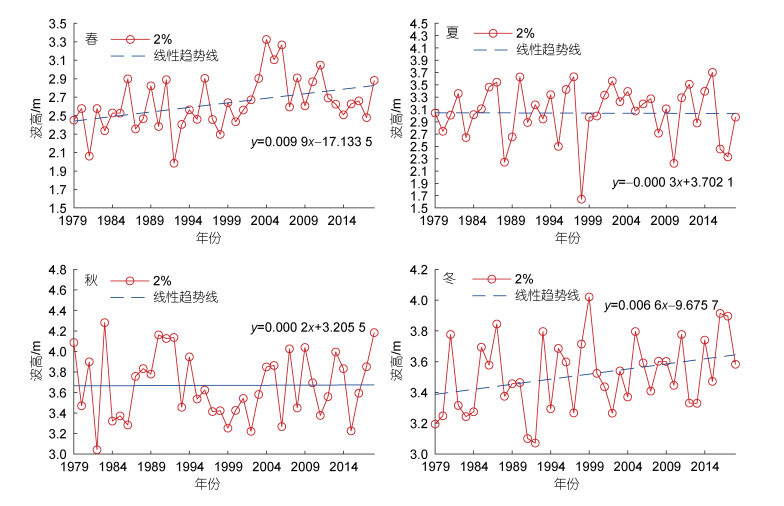 |
| 图 6 1979~2018年极端波高季节变化趋势图 Fig. 6 Seasonal trend of extreme wave height from 1979 to 2018 |
本文使用Niño3.4区域平均的海表面温度异常作为厄尔尼诺指数。根据中国气象局颁布的《厄尔尼诺/拉尼娜事件判定方法》, 定义Niño3.4指数≥0.5 ℃并持续5个月以上为一次厄尔尼诺事件, Niño3.4指数≤−0.5 ℃并持续5个月以上为一次拉尼娜事件。另外, 定义事件峰值强度绝对值达到或超过2.5 ℃的事件为超强事件。为研究ENSO的影响, 本文利用美国国家海洋和大气管理局(National Oceanic and Atmospheric Administration, NOAA)-气候预测中心(Climate Prediction Center, CPC)(https://www.cpc.ncep.noaa.gov/data/indices/ersst5.nino.mth.81-10.ascii)每月的Niño3.4指数(海表面温度在5°S~5°N, 170°~120°W上的平均异常, 基于ERST.v5计算)进行研究分析。从图 7可看出1979~2018年的厄尔尼诺指数。根据厄尔尼诺事件的定义, 1979~2018年共发生了10次厄尔尼诺事件和10次拉尼娜事件, 其中1982/1983、1986/1987、1991/1992、1994/1995、1997/1998、2002/2003、2004/2005、2006/2007、2009/2010、2015/2016为厄尔尼诺事件; 1983/1984、1984/1985、1988/1989、1995/1996、1998/2000、2005/2006、2007/2008、2010/2011、2011/2012、2017/2018为拉尼娜事件。其中, 2015/2016年厄尔尼诺事件峰值强度为2.8 ℃, 是一次超强厄尔尼诺事件。
 |
| 图 7 1979~2018年厄尔尼诺系数(Niño3.4)统计 Fig. 7 Statistics of El Nino coefficient (Niño3.4) from 1979 to 2018 |
极值理论(extreme value theory, EVT)是统计学的重要分支之一, 在气象和水文极端中得到了广泛的应用(Shinyie et al, 2013; Vasiliades et al, 2015)。极值统计中有两个最基本的分布, 广义极值分布(generalized extreme value, GEV)和广义帕累托分布(generalized Pareto distribution, GPD)。GEV分布用统一的形式来表示Gumbel分布、Frechet分布和Weibull分布三种极值分布类型, 通常选取数据中的“年最大值”或“区组最大值”数据来建立模型。GEV累积分布函数F表示为
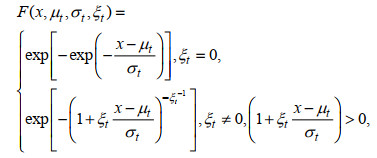 (1)
(1)其中, μt, σt, ξt分别为位置参数、尺度参数和形状参数。我们采用最大似然法进行Kolmogorov-Smirnov检验, 以确保该时期的波浪极端与GEV模型吻合良好。为了检验气候变化对季节极端值的影响, 使用了一个气候变率指数ν (本研究中的ENSO指数)作为GEV参数的协变量。以往的研究发现, 气候变率对极端值的影响主要是通过位置参数, 而尺度和形状参数几乎没有影响。因此, 本文仅考虑位置参数μt随时间(t)的变化:
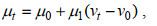 (2)
(2)其中, vt和v0分别为t时刻和t0时刻的气候变率指数, μ0为t0时刻的位置参数, μ1为位置参数回归系数。
3.2.2 研究区域极端波高与厄尔尼诺系数相关性分析 3.2.2.1 相关性年空间分布厄尔尼诺现象的变化通过地理位置参数的变化使GEV分布发生左右偏移, 在栅格基础上对波高进行GEV分析, 得出位置参数回归系数μ1[公式(2)]的空间分布(图 8)。图 8显示了1979~2018年厄尔尼诺对全年极端波高的影响, 图中显示了极端波高的GEV位置参数[公式(2)中的μ1]回归系数对全年Niño3.4指数的空间分布。在这期间, 南海大部分地区出现了显著的正相位, 黄海北部和东北部出现正相位, 而东海大部分地区以及黄海西南部则出现了相反的相位。这与Kumar等(2016)基于不同时期ERA-Interim和ERA-20C数据集研究全球极值波浪与气候变化之间的关联性时的发现一致。
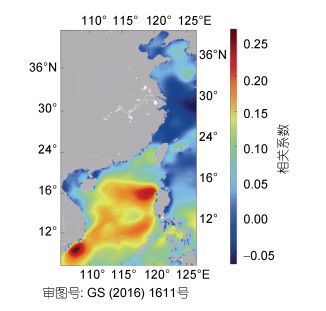 |
| 图 8 1979~2018年相关性年空间分布 Fig. 8 Spatial distribution of correlation years from 1979 to 2018 |
Niño3.4极端波响应模式的季节变化如图 9所示。GEV分析使用位置参数和Niño3.4的回归系数季节平均指数。显著的厄尔尼诺事件影响全年持续, 并且在不同季节的空间范围有所不同。春季中国渤海、黄海以及太平洋西部地区受气候指数影响大; 在夏季, 气候指数对南海东南部、东海东部及南部影响较大; 在秋季, 南海北部地区可以看到强烈的气候指数影响; 冬季期间, 黄海东南部、东海部分海域、渤海地区、台湾海峡西侧及西沙群岛周边海域受气候指数影响较大。结合2.2.1中极端波高季节趋势变化分布, 可以看出在厄尔尼诺现象影响大的地区极端波高普遍具有较大幅度波动。
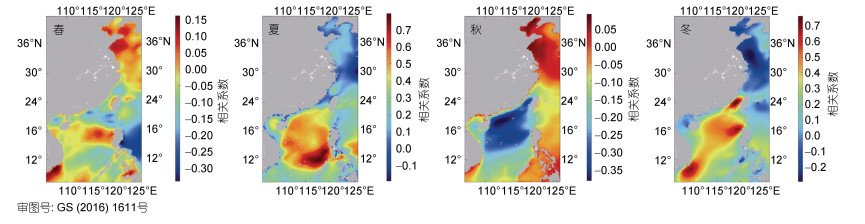 |
| 图 9 1979~2018年相关性四季空间分布 Fig. 9 Spatial distribution of correlation in four seasons from 1979 to 2018 |
基于研究海域ERA5后报资料, 本文详细分析了2%极端波浪的空间分布情况、长期年均变化趋势及变化趋势的空间分布情况, 极端波浪季节分布、趋势变化空间分布以及极端波浪的季均变化趋势和厄尔尼诺系数变化, 并通过GEV极值波高与厄尔尼诺系数回归方程结合分析得出厄尔尼诺现象对极端波高的影响分布, 结果表明:
(1) 由2%极端波高的数值年际变化可以看出, 在长期变化趋势中, 本文研究海域2%极端波浪年均值在3~4 m间浮动, 且整体趋势递增, 其中1988和1996年波高值出现的波动最为显著。渤海及黄海海域的极端波高年均值约在3 m, 东海南部、台湾海峡周边及南海东北部海域极端波高年均值较大, 约在5~6 m。
在四季趋势变化中, 春夏极端波高增长趋势较秋冬高, 且波动明显。春季在1.9~3.5 m之间且整体波高较小, 其中在1991、1996、2005、2006和2011年波动明显, 幅度最显著时能达到1 m; 夏季波浪高度波动明显, 极端波高在1.5~3.9 m左右, 其中1987、1988、1998、2010和2015年波动值显著, 最大可达到2 m左右。春季和夏季的季节均值极端波高较秋季和冬季小, 春季大部分海域极端波高在3.5~4 m左右; 夏季和秋季极端波高变化趋势较春季和冬季相对平缓; 秋季研究海域较大值集中在东海南部和南海中北部; 冬季整个研究区域极端波高值普遍较高, 大部分海域极端波高在4~4.5 m左右。
结合厄尔尼诺系数变化趋势和极端波高的数值年际变化, 极端波高出现显著波动值的1988和1995年可以看到, 1994和1995年都发生了厄尔尼诺和拉尼娜现象, 且1987年整年都为厄尔尼诺现象; 而在四季极端波高有较大波动时大多伴随着厄尔尼诺或是拉尼娜现象的发生。
(2) 在2%极端波高年际趋势变化分布中, 南海与东海为增长趋势, 渤海海域及黄海部分海域呈下降趋势。在极端波高季节际趋势变化分布中, 春季和冬季渤海及黄海呈下降趋势, 太平洋西部地区和南海大部分地区则为增长趋势; 在夏季, 南海西南部为下降趋势, 而台湾岛东部为明显增长; 秋季台湾岛东北部及东海中南部增长趋势, 南海西南部为下降趋势。
(3) 在极端波高的GEV位置参数对全年Niño3.4指数回归系数的空间分布中, 东海大部分海域及南海海域受气候变量影响较大; 在不同季节回归系数分布中, 夏秋冬季气候变量对南海的影响较大, 冬春对东海海域影响较大。结合厄尔尼诺现象对GEV分布中位置参数的影响分布图和极端波高年、季节际趋势变化分布图, 可以看出在厄尔尼诺现象影响大的地区极端波高普遍具有较大幅度波动。
乔守文, 孙嘉诚, 石洪源, 等, 2020. 基于ERA5的黄渤海附近海域波浪能资源时空特征分析. 海洋与湖沼, 51(6): 1350-1358 |
李文博, 张坤兰, 吴克俭, 2017. 基于卫星资料的南海波候特征研究. 海洋湖沼通报, (6): 11-20 DOI:10.13984/j.cnki.cn37-1141.2017.06.002 |
李朝, 侯一筠, 李水清, 等, 2021. 两类典型台风路径影响下的黄、渤海海浪场特征研究. 海洋与湖沼, 52(1): 51-65 |
吴迪茜, 陈智杰, 2021. 平潭岛东部海域波浪特征及波浪能分析. 应用海洋学学报, 40(2): 293-302 |
邱文博, 李冠宇, 徐俊臣, 等, 2021. 黄渤海海域波浪时空变化特征分析. 海洋科学, 45(7): 1-8 |
郑崇伟, 林刚, 邵龙潭, 2013. 1988-2010年中国海大浪频率及其长期变化趋势. 厦门大学学报(自然科学版), 52(3): 395-399 |
BROMIRSKI P D, CAYAN D R, HELLY J, et al, 2013. Wave power variability and trends across the North Pacific. Journal of Geophysical Research: Oceans, 118(12): 6329-6348 DOI:10.1002/2013JC009189 |
DODET G, BERTIN X, TABORDA R, 2010. Wave climate variability in the North-East Atlantic Ocean over the last six decades. Ocean Modelling, 31(3/4): 120-131 DOI:10.1016/j.ocemod.2009.10.010 |
HEMER M A, CHURCH J A, HUNTER J R, 2010. Variability and trends in the directional wave climate of the Southern Hemisphere. International Journal of Climatology, 30(4): 475-491 DOI:10.1002/joc.1900 |
IZAGUIRRE C, MÉNDEZ F J, MENÉNDEZ M, et al, 2011. Global extreme wave height variability based on satellite data. Geophysical Research Letters, 38(10): L10607 DOI:10.1029/2011GL047302 |
KUMAR P, KAUR S, WELLER E, et al, 2019. Influence of natural climate variability on the extreme ocean surface wave heights over the Indian Ocean. Journal of Geophysical Research: Oceans, 124(8): 6176-6199 DOI:10.1029/2019JC015391 |
KUMAR P, MIN S K, WELLER E, et al, 2016. Influence of climate variability on extreme ocean surface wave heights assessed from ERA-interim and ERA-20C. Journal of Climate, 29(11): 4031-4046 DOI:10.1175/JCLI-D-15-0580.1 |
MENÉNDEZ M, MÉNDEZ F J, LOSADA I J, et al, 2008. Variability of extreme wave heights in the northeast Pacific Ocean based on buoy measurements. Geophysical Research Letters, 35(22): L22607 DOI:10.1029/2008GL035394 |
PATRA A, BHASKARAN P K, 2016. Trends in wind-wave climate over the head Bay of Bengal region. International Journal of Climatology, 36(13): 4222-4240 DOI:10.1002/joc.4627 |
PATRA A, BHASKARAN P K, 2017. Temporal variability in wind-wave climate and its validation with ESSO-NIOT wave atlas for the head Bay of Bengal. Climate Dynamics, 49(4): 1271-1288 DOI:10.1007/s00382-016-3385-z |
PATRA A, MIN S K, SEONG M G, 2020. Climate variability impacts on global extreme wave heights: seasonal assessment using satellite data and ERA5 reanalysis. Journal of Geophysical Research: Oceans, 125(12): e2020JC016754 DOI:10.1029/2020JC016754 |
SHI H Y, CAO X F, LI Q J, et al, 2021. Evaluating the accuracy of ERA5 wave reanalysis in the water around China. Journal of Ocean University of China, 20(1): 1-9 DOI:10.1007/s11802-021-4496-7 |
SHINYIE W L, ISMAIL N, JEMAIN A A, 2013. Semi-parametric estimation for selecting optimal threshold of extreme rainfall events. Water Resources Management, 27(7): 2325-2352 |
STOPA J E, CHEUNG K F, TOLMAN H L, et al, 2013. Patterns and cycles in the Climate Forecast System Reanalysis wind and wave data. Ocean Modelling, 70: 207-220 DOI:10.1016/j.ocemod.2012.10.005 |
VASILIADES L, GALIATSATOU P, LOUKAS A, 2015. Nonstationary frequency analysis of annual maximum rainfall using climate covariates. Water Resources Management, 29(2): 339-358 |
WANG X L, FENG Y, SWAIL V R, 2012. North Atlantic wave height trends as reconstructed from the 20th century reanalysis. Geophysical Research Letters, 39(18): L18705 DOI:10.1029/2012GL053381 |
 2022, Vol. 53
2022, Vol. 53


