中国海洋湖沼学会主办。
文章信息
- 陈晓, 刘长华, 刘志亮, 王旭, 王春晓, 贾思洋. 2022.
- CHEN Xiao, LIU Chang-Hua, LIU Zhi-Liang, WANG Xu, WANG Chun-Xiao, JIA Si-Yang. 2022.
- 2010~2019年北黄海海域长序列海量温盐数据分析与处理方法
- ANALYSIS AND PROCESSING OF LONG SEQUENCE AND MASSIVE TEMPERATURE AND SALINITY DATA OF THE NORTH YELLOW SEA FROM 2010 TO 2019
- 海洋与湖沼, 53(1): 49-61
- Oceanologia et Limnologia Sinica, 53(1): 49-61.
- http://dx.doi.org/10.11693/hyhz20210700170
文章历史
-
收稿日期:2021-07-29
收修改稿日期:2021-10-06
2. 中国科学院海洋研究所 山东青岛 266071;
3. 河北省海洋动力过程与资源环境重点实验室 河北秦皇岛 066004
2. Institute of Oceanology, Chinese Academy of Sciences, Qingdao 266071, China;
3. Hebei Key Laboratory of Ocean Dynamics, Resources and Environments, Qinhuangdao 066004, China
随着信息化和电子通信等技术的迅猛发展, 我国已经建立了海-陆-空全方位立体式的海洋观测系统(黄冬梅等, 2016)。通过船舶走航、观测浮标、海岛陆基和遥感卫星等方式(Liu et al, 2016), 已经获取到海量、异构且多源的观测数据(钱程程等, 2018), 为“透明海洋”和“智慧海洋”的构建奠定了坚实基础, 也对深入了解和认知海洋、推动海洋科学发展等具有重要意义和价值。
观测浮标作为重要、成熟、可靠的实时获取海洋环境数据的观测手段之一, 具有成本低、寿命长、布放灵活、长期连续监测、自动采集和实时发送数据等突出优势(刘长华等, 2019a)。即使在恶劣环境或其他现场监测手段难以实施的情况下, 浮标仍可采集到水文、水质和气象等海洋综合环境数据, 为我国海洋经济、海上军事、海洋灾害预报和海洋生态环境等方面提供了重要的数据支撑和保障(赵聪蛟等, 2016)。
然而, 由于海洋环境恶劣、通信限制、能源供给不足, 以及渔业生产无序、甚至人为破坏等原因, 造成近海浮标观测系统的长期稳定性下降, 在一定程度上影响浮标观测数据连续有效的获取(刘长华等, 2020), 导致获取到的海量观测数据存在异常和缺失等情况。如果直接对获取到的整个原始数据集(包含异常或缺失的数据集)进行分析与挖掘, 会使研究结果与客观现实存在较大偏差, 从而影响海洋防灾减灾和生态环境保护等辅助决策的精准性。现有研究表明, 由于海洋观测环境多变, 现场观测维护困难等原因, 很难通过现场补救观测解决数据中存在的异常和缺失情况。因此, 需要采用数据后处理技术, 减小设备自身和人为因素导致的数据误差, 甚至数据补缺, 提高海上现场观测数据的有效性和准确性, 进而有效提升数据分析的辅助决策能力。
目前, 数据的异常检测(张良均等, 2018; 卢勇夺等, 2019; 张宇等, 2020)和缺失补全(Chen et al, 2014; Benmarhnia et al, 2015; Zhang et al, 2015; Qin et al, 2019; 陈海洋等, 2020; 孙晓丽等, 2021)普遍存在于各个科研领域, 国内外专家和学者已开展了大量研究。针对海洋浮标数据, 主要基于经验常识、数据检验标准库和统计理论[如极值法、格拉布斯(Grubbs)准则、狄克逊(Dixon)准则和拉依达准则等]方法识别数据中的异常值。如, 刘首华等(2016)结合格拉布斯准则、局地异常值检验方法和波高观测误差控制建立了一种实用的波高数据异常值的质控方法。卢勇夺等(2019)综合运用极值法则、莱以特(拉依达)法则、局部法则和观测误差控制, 基于锚系浮标QF110和QF306中海面风速、气温、有效波高等数据, 初步提出了浮标异常值检测方法。当数据满足某种分布假设时, 上述基于统计分析的方法在对单一参数的异常检测中具有较好的效果。针对海洋浮标数据, 通常采用稀疏数据插值(如线性插值、Kriging插值和最优插值等)、数据重构和数据插补(如统计学插补和机器学习插补等)方法实现缺失数据补全。刘宇(2020)基于单层LSTM (long short-term memory)长短时记忆神经网络模型和GRU (gate recurrent unit)神经网络模型提出了LSTM-GRU联合多层神经网络提高了Argo历史数据补全的准确率。随着信息科学技术的不断发展, 基于遗传算法、聚类和神经网络模型等异常和缺失数据的处理方法不断涌现; 然而, 上述方法的参数设置(如聚类个数、神经元个数和神经网络层数等)对模型有显著影响。因此, 本文选择经典的、具有普适性的统计学理论, 结合矩阵运算等数学方法和信息技术从而解决浮标水温和盐度数据中的异常和缺失问题。
为了深入了解北黄海长海县附近海域特征, 掌握温盐年月时间序列的线性变化趋势与相关关系等, 本文基于中国科学院近海观测研究网络黄海站位于北黄海长海县附近海域的五套浮标2010~2019年连续10 a的长序列海量观测数据, 针对海洋表层水温和盐度的数据特点, 给出适合该数据的异常检测及插补方法。首先分析水温和盐度数据并标定异常; 其次对浮标自身缺失和删除异常后的温盐缺失数据进行逐月插补; 最后验证上述方法的有效性。本研究成果可为海上现场观测数据后期处理提供借鉴, 为海洋科学研究服务。
1 数据与方法 1.1 数据 1.1.1 研究数据研究数据来源于中国科学院近海海洋观测研究网络黄海站的五套浮标(刘长华等, 2017, 2018, 2019b)。主要观测区域是北黄海大连长海县附近海域, 如图 1所示, 其经度范围为122°35′~ 123°06′E, 纬度范围为38°45′~39°16′N。
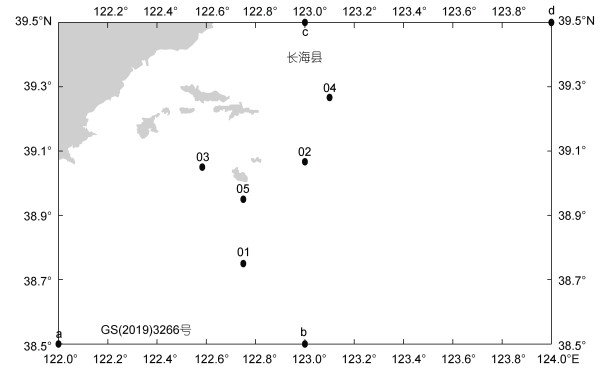 |
| 图 1 浮标分布与坐标点 Fig. 1 Distribution of buoys and coordinate points 注: 01~05表示研究数据中五个浮标号; a~d表示对比数据中4个坐标点 |
五套浮标的基本信息如表 1所示。其中, 01号为直径3 m的圆盘形海洋综合观测浮标, 是该海域的核心浮标, 包含气象(如气温、湿度、气压、风速风向和能见度等)、水文(如波浪、水温、盐度和剖面海流等)和水质(如浊度、叶绿素和溶解氧等)等参数; 02~04号为直径2 m的圆盘形海洋常规观测浮标, 05号为直径2 m的自容垂直剖面链式观测浮标, 这4套浮标包含了水文和水质的相关参数。其中, 温盐是反映物理海洋学特性的重要参数(张博等, 2018; 张翠翠等, 2020), 是海洋水文观测的基本要素, 对认知与研究海洋具有重要意义。
| 浮标号 | 布放位置 | 类型 | 时间范围 | 数据量/条 | ||||
| 经度 | 纬度 | 开始时间 | 结束时间 | 水温 | 盐度 | |||
| 01 | 122°45'E | 38°45'N | 3 m综合 | 2010年01月23日 | 2019年10月05日 | 131 756 | 123 017 | |
| 02 | 123°00'E | 39°04'N | 2 m常规 | 2010年01月04日 | 2019年10月18日 | 89 413 | 78 841 | |
| 03 | 122°35'E | 39°03'N | 2 m常规 | 2010年01月03日 | 2019年09月15日 | 186 213 | 176 019 | |
| 04 | 123°06'E | 39°16'N | 2 m常规 | 2010年01月04日 | 2019年09月26日 | 60 145 | 59 470 | |
| 05 | 122°45'E | 38°57'N | 2 m垂直剖面 | 2010年01月26日 | 2019年12月31日 | 71 967 | 71 487 | |
五套浮标于2009年6月完成布放并投入使用, 至今已连续获取了近12 a的数据, 目前数据累积仍在持续进行中。本文选取了五套浮标2010~2019年连续10 a的海洋表层水温和盐度数据作为研究对象, 数据总量为1 048 328条; 不同浮标数据的时间范围略有不同, 如表 1所示。原始数据集包含了50个以年度为单位的表格型数据文件(*.xls), 每个文件中均包含日期时间、水温和盐度3列数据; 其中, 日期时间为文本型数据、水温和盐度为数值型数据。同一浮标在不同时期的数据发送频率不同, 主要包括1次/10 min、1次/30 min和1次/60 min三种情况。
当浮标设备被海洋生物附着等情况下会采集到异常数据; 在浮标维修期间会产生缺失数据。其中, 异常数据主要分为2种情况, 一是跳变型异常数据, 如盐度数据在正常范围内, 突然增大或减少, 且在下一时刻还恢复到正常范围, 如图 2a和2b所示; 二是渐变型异常数据, 如盐度数据从30开始逐渐下降到20, 如图 2c所示。因此, 为了保障数据挖掘与分析结果的准确性, 有必要选取有效的方法对数据进行处理, 进而提升数据质量。
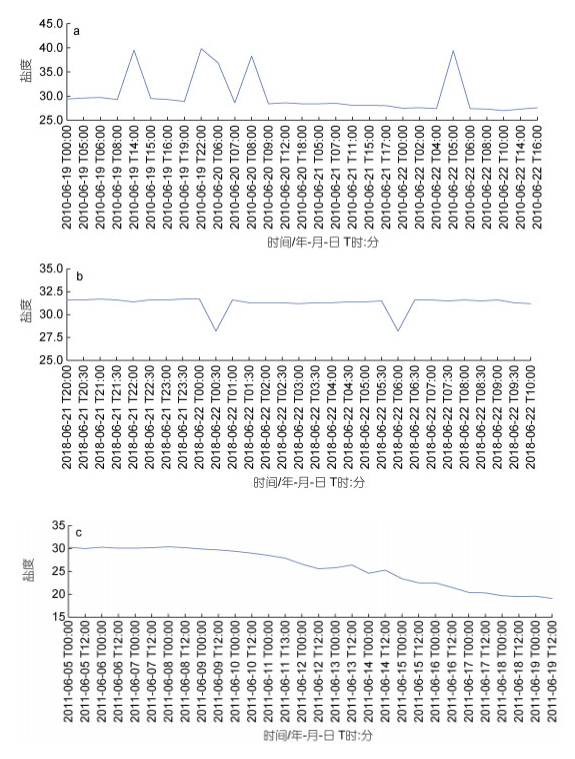 |
| 图 2 数据异常情况 Fig. 2 Data anomalies 注: a: 跳变型-变大; b: 跳变型-变小; c: 渐变型 |
对比数据来源于国家海洋和大气管理局/国家环境信息中心(National Oceanic and Atmospheric Administration/National Centers for Environmental Information, NOAA/NCEI)世界海洋数据库(World Ocean Database, WOD)中的海洋水温和盐度; 数据下载链接为http://159.226.119.60/cheng/。该数据集的时间范围是1940年至今, 时间分辨率为月平均数据, 空间分辨率为1°×1°, 垂直范围为0~2 000 m, 41层, 覆盖范围为全球海洋。本文从中选取了与研究数据对应的时空数据, 为2010年1月至2019年12月4个坐标点(图 1中a、b、c和d, 坐标分别为122°E/38.5°N、123°E/38.5°N、123°E/39.5°N、124°E/39.5°N)第1层的海洋温盐数据。
1.1.3 数据统计与汇总基于五套浮标获取到的原始温盐数据集, 先对数据做整体分析并标定异常; 再基于剔除异常后的数据集, 分别统计五套浮标温盐数据每个月的最大值、最小值和平均值, 得到10 a每年12个月的温盐时间序列; 在此基础上, 五套浮标对应月份的温盐数据再求平均值, 可得到研究海域的时间序列。为了分析温盐的季节和年际变化特征, 通常还会将数据按年月进行汇总。其中, 每行是一年的数据, 每列是某个月份的数据; 每年每月又分别包含其最大值、最小值和平均值的相关数据; 若按行求平均值, 即可得到年平均数据; 若按列求平均值, 即可得到10 a累计的月平均数据。
在对比数据中, 对4个坐标点的10 a每年12个月的温盐时间序列求平均值, 得到该海域的时间序列; 与研究数据同理按年月进行汇总。
1.2 方法 1.2.1 异常数据分析方法异常数据分析方法主要分为简单统计分析、拉依达准则和箱型图等3类方法(张良均等, 2018)。
简单统计指标主要包括: 最大值、最小值、均值、中位数和众数等。该方法, 采用上述指标对数据集中每列(属性)数据分别进行描述性统计, 掌握数据的基本结构和特征。最常采用最大值和最小值来判断数据是否超出了合理的范围, 又称为极值法(卢勇夺等, 2019)。
拉依达准则, 又称为莱以特法则, 通常采用均值μ和标准差σ来判断数据是否超出了合理的范围。数值分布在(μ±σ), (μ±2σ)和(μ±3σ)中的概率分别为68.27%, 95.44%和99.74%。其中, 基于(μ±2σ)和(μ±3σ)确定界限的方法又分别称为2σ原则和3σ原则。
箱型图, 又称为箱线图或盒式图, 通常先对数据从小到大排序, 再采用四分位法通过上下界(Q1-1.5×Q, Q3+1.5×Q)判断数据是否超出了合理的范围; 式中, Q1和Q3分别表示第一(25%)和第三(75%)个四分位数; Q=Q3-Q1表示第一至第三个位数间的距离。
上述方法各有特色和优缺点。其中, 拉依达准则假设数据服从正态分布, 但以此计算的平均值和标准差耐抗性极小, 异常值会对其产生较大影响, 从而导致无法获取所有异常数据。然而真实数据往往并不严格服从正态分布, 此时可采用箱型图法, 它无需考虑数据的分布特征, 对异常数据的分析比较客观, 且具有一定的鲁棒性。在具体应用中, 可根据实际情况选取不同方法, 从而确定数据的上下界限。
1.2.2 缺失数据处理方法缺失数据的处理方法主要分为不处理、删除和数据插补等3类方法(张良均等, 2018)。其中, 不处理, 即直接在包含空值的数据集上进行分析或研究; 删除法(Faria et al, 2014), 先将存在缺失值的对象(记录或元组)删除, 再将剩余数据看作一个“完整”的数据集; 数据插补法(Chan et al, 2003; Skrondal et al, 2014; Lguensat et al, 2016), 采用某种策略对缺失值进行填充, 从而得到一个“完备”的数据集。
数据插补法又可分为统计学插补法(如均值插补、回归插补和热卡插补等)和机器学习插补法(如自组织映射插补法和支持向量机插补法等)。本节仅介绍与本文密切相关的插补方法, 如下。线性插补(linear interpolation)是指使用连接2个已知量的直线来确定在这2个已知量之间的一个未知量的方法。三次样条插补(cubic spline interpolation)作为最常用的分段多项式方法, 数学上通过求解三弯矩方程组得出曲线函数组的过程; 该方法具有较好的稳定性和收敛性, 但曲线的光滑性较差。拉格朗日插补(Lagrange interpolation)是基于多项式和基函数的插补方法; 该方法具有较高的区间内插值精确度, 但其计算复杂度较高。最近邻(K near neighbor, KNN)插补采用相邻K个数据特征的均方差填充缺失值。核范数最小化(nuclear- norm minimization, NNM)插补采用凸优化找到匹配观测值的低秩解来填充缺失值, 该方法计算效率较慢。迭代软阈值插补(SoftImpute)采用奇异值分解(singular value decomposition, SVD)处理填充缺失值; 令A=UDVT, 其中U和V为酉矩阵, D为主对角线矩阵, 对角线元素为奇异值; 该方法适合稀疏矩阵, 且具有较高的效率。IterativeImputer采用循环方式将具有缺失值的每个特征建模为其他特征的函数来估算缺失值; 该方法在每个步骤中, 将特征目标列指定为输出y, 将其他列视为输入X, 使用一个回归器来在未缺失样本上对(X, y)进行拟合; 再使用这个回归器预测缺失值y; 重复迭代, 将最后一轮的计算结果返回; 该方法合适在缺失数据较多、又不能删除缺失值所在行列数据时使用。
实际应用中, 仍需要根据数据特点和目标, 选取适合的具体方法。在本书研究中, 数据的汇总形式类似于矩阵, 适用基于统计学理论和矩阵运算等数学方法实现缺失插补。本文不仅要实现缺失数据的插补, 还要保障各月插补后的数据间的大小关系, 即: 最大值≥平均值≥最小值。
1.2.3 K-折交叉验证与评价指标K-折交叉验证(K-fold cross validation)作为数据模型有效性的验证方法之一, 在预测、聚类和分类等任务中得到广泛应用。在K-折交叉验证中, 首先将数据集平均分为K份, 其中K-1份作为训练集、1份作为测试集; 其次, 采用训练集构建模型; 最后, 通过测试集对模型的效果进行评估。重复K次, 即将每1份均作为测试集1次, 为一次K-折交叉验证。
均方误差(mean squared error, MSE)和决定系数(R-square, R2)是评价预测模型/算法的常用指标, 本文采用MSE和R2对插补方法(模型)进行评价。其中, MSE是模型效能最常用的评价指标, 通过计算真实值与预测值之间的均方差来评价模型, 其值越小模型稳定性越好。R2∈[0, 1]是模型拟合效果的评价指标, 其值越接近于1模型的拟合效果越好; 通常情况下, R2达到0.4即可满足应用需求。
2 温盐异常数据处理 2.1 温盐原始数据的统计与分析为了检测原始温盐数据中是否存在不合常理的数值(异常值), 需采用简单统计分析指标(如最大值、最小值、平均值以及标准差等)对数据进行整体分析。其本质是通过统计分析确定数据的上下界限, 从而识别出异常数据。在北黄海长海县附近海域中, 由最小值和最大值可见, 五套浮标总体的水温范围是[-7.20 ℃, 40.00 ℃]、盐度范围是[0.00, 62.40]。
目前, 已有一些关于黄海温盐分布与特征分析的研究(鲍献文等, 2009; 石强, 2013, 2014, 2016, 2019; 齐庆华等, 2019)。如, 鲍献文等(2009)基于2006~2007年北黄海数据指出, 海洋表层水温在冬春夏秋四季的范围分别为2.00~9.00 ℃、7.50~11.00 ℃、19.00~25.00 ℃和17.00~19.50 ℃, 海洋表层盐度在冬春夏秋四季的范围分别为30.00~32.60, 27.00~32.40, 29.00~31.80和28.00~32.20。基于1977~2012/2013年历年2月份数据指出, 北黄海海洋表层水温和盐度在冬季的范围分别为0.29~5.89 ℃和30.70~32.45 (石强, 2013), 南黄海海洋表层水温和盐度在冬季的范围分别为1.25~8.90 ℃和30.70~32.96 (石强, 2014)。基于1976~2015/2016年历年7~8月份数据指出, 北黄海海洋表层水温和盐度在夏季的范围分别为22.00~26.00 ℃和30.60~32.10 (石强, 2016), 南黄海海洋表层水温和盐度在夏季的范围分别为25.00~28.50 ℃和30.80~32.20 (石强, 2019)。综上, 依据文献历史资料, 黄海海域水温和盐度四季范围大约为0.29~28.50 ℃和27.00~32.96。同时, 在Cheng等(2017, 2021)提供的全球海洋温盐数据中获取了2010~2019年北黄海海域中月平均温盐数据, 统计汇总得到全年表层水温和盐度范围分别为0.97~25.41 ℃和29.97~34.07。由此可见, 该研究海域的五套浮标中获取的原始温盐数据中存在异常。因此, 需进一步采用拉依达准则(2σ原则和3σ原则)和箱型图法进行分析, 并确定温盐数据的界限, 结果如表 2所示。
| 特征 | 方法 | 01 | 02 | 03 | 04 | 05 | 平均值 | |
| 水温/℃ | 2σ原则 | 下界 | -1.88 | -3.04 | -3.70 | -4.29 | -1.68 | -2.92 |
| 上界 | 31.24 | 31.21 | 27.44 | 29.48 | 30.98 | 30.07 | ||
| 3σ原则 | 下界 | -10.16 | -11.60 | -11.49 | -12.73 | -9.84 | -11.16 | |
| 上界 | 39.52 | 39.78 | 35.22 | 37.92 | 39.15 | 38.32 | ||
| 箱型图法 | 下界 | -16.40 | -19.70 | -17.80 | -19.20 | -15.90 | -17.80 | |
| 上界 | 45.20 | 46.70 | 41.40 | 44.00 | 44.90 | 44.44 | ||
| 盐度 | 2σ原则 | 下界 | 18.88 | 21.78 | 19.60 | 18.75 | 17.98 | 19.40 |
| 上界 | 41.19 | 38.12 | 38.28 | 39.51 | 41.26 | 39.67 | ||
| 3σ原则 | 下界 | 13.31 | 17.70 | 14.92 | 13.56 | 12.16 | 14.33 | |
| 上界 | 46.77 | 42.20 | 42.95 | 44.70 | 47.08 | 44.74 | ||
| 箱型图法 | Q | 1.21 | 1.58 | 3.70 | 2.90 | 1.50 | ||
| 下界 | 28.98 | 27.75 | 22.25 | 24.25 | 28.15 | 26.28 | ||
| 上界 | 33.82 | 34.07 | 37.05 | 35.85 | 34.15 | 34.99 | ||
| 注: 01~05表示浮标序号 | ||||||||
对于五套浮标的水温数据, 由表 2可见, 基于箱型图法和3σ原则的平均上下界限分别为[-17.80 ℃, 44.44 ℃]和[-11.16 ℃, 38.32 ℃]。这2个界限超过了水温数据的极值范围, 显然是不合理的。基于2σ原则的平均上下界限为[-2.92 ℃, 30.07 ℃], 该界限介于水温数据的极值范围之间, 且与文献资料中数据较接近。可见, 水温属于正态分布数据, 适合用2σ原则确定上下界。
对于五套浮标的盐度数据, 由表 2可见, 基于2σ原则和3σ原则的平均上下界限分别为[19.40, 39.67]和[14.33, 44.47]。这个界限虽然介于盐度数据的极值范围, 但与文献中数据不相符。与此相比, 基于箱型图法的平均上下界限为[26.28, 34.99], 较为合理。可见, 盐度数据适合用箱型图法确定上下界。
通过对五套浮标温盐原始数据的统计与分析, 综合考虑文献和相关数据资料, 确定水温界限为[0.00 ℃, 31.00 ℃]、盐度界限为[27.00, 34.00]。同时, 水温小于0.00 ℃或大于31.00 ℃、盐度小于27.00或大于34.00的数据均标记为异常数据。
2.2 温盐异常数据的处理与验证异常数据处理主要分为不处理、平均值修正、视为缺失值和删除等四种方法(张良均等, 2018)。由表 2可见, 异常数据会影响原始数据的结构分布、平均值等的计算结果。为了减少对后续数据挖掘与分析质量的影响, 又考虑到浮标数据的发送频率较高, 连续10 a已经获取了大量数据; 因此, 本文将异常数据视为缺失值, 待后续与原始缺失数据一起处理。
为了验证温盐界限的合理性, 对剔除异常后的数据集, 采用2σ原则和箱型图法进行了数据统计, 如表 3所示。由表 3可见, 基于2σ原则的水温界限为[-2.84 ℃, 30.02 ℃], 基于箱型图法的盐度界限为[28.78, 33.64], 这2个界限均与文献资料中的范围比较接近。同时, 五套浮标盐度的Q值分别为1.00、1.20、1.30、1.40和1.18, 与表 2中Q值相比, 较为接近且合理。综上, 五套浮标水温界限[0.00 ℃, 31.00 ℃]和盐度界限[27.00, 34.00]是合理的。
| 特征 | 方法 | 01 | 02 | 03 | 04 | 05 | 平均值 | |
| 水温/℃ [0.00, 31.00] |
2σ原则 | 下界 | -1.83 | -2.92 | -3.63 | -4.19 | -1.61 | -2.84 |
| 上界 | 31.23 | 31.03 | 27.44 | 29.45 | 30.95 | 30.02 | ||
| 盐度 [27.00, 34.00] |
箱型图法 | Q | 1.00 | 1.20 | 1.30 | 1.40 | 1.18 | |
| 下界 | 29.50 | 28.80 | 28.45 | 28.10 | 29.05 | 28.78 | ||
| 上界 | 33.50 | 33.60 | 33.65 | 33.70 | 33.77 | 33.64 | ||
数据有效率即为有效数据量占全部数据量的比例。在五套浮标中, 剔除水温和盐度的异常数据后, 按总体、年和月等3种方式对温盐数据有效率进行统计分析。五套浮标温盐总体数据有效率统计结果, 如表 4所示; 水温和盐度的年、月数据有效率统计, 如图 3所示。
| 特征 | 浮标号 | 异常数据量/条 | 有效数据量/条 | 有效率 | 平均值 |
| 水温/℃ | 01 | 146 | 131610 | 99.89% | 99.76% |
| 02 | 356 | 89057 | 99.60% | ||
| 03 | 548 | 185665 | 99.71% | ||
| 04 | 151 | 59994 | 99.75% | ||
| 05 | 106 | 71861 | 99.85% | ||
| 盐度 | 01 | 9245 | 113772 | 92.48% | 84.15% |
| 02 | 9712 | 69129 | 87.68% | ||
| 03 | 45010 | 131009 | 74.43% | ||
| 04 | 13394 | 46076 | 77.48% | ||
| 05 | 8077 | 63410 | 88.70% |
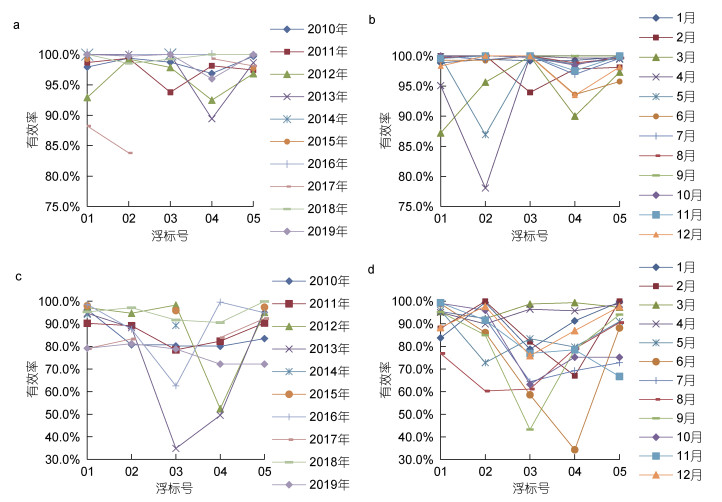 |
| 图 3 温盐数据有效率统计 Fig. 3 Data efficiency of temperature and salinity 注: a: 年水温有效率; b: 月水温有效率; c: 年盐度有效率; d: 月盐度有效率 |
对于温盐数据, 如表 4所示, 从总体上看五套浮标的平均有效率分别达到99.76%和84.15%。在图 3a中, 除2017年01和02号浮标、2013年04号浮标外, 其余年度水温数据的平均有效率均超过90.00%; 在图 3b中, 除4月02号浮标、3月01号浮标和5月02号浮标外, 其余月份水温数据的平均有效率均超过85.00%。在图 3c中, 除2013年03和04号浮标、2012年04号浮标外, 其余年度盐度数据的平均有效率均超过60.00%; 在图 3d中, 除6月03和04号浮标、9月03号浮标外, 其余月份盐度数据的平均有效率均超过60.00%。五套浮标中, 水温数据有效率较高、均达到99.50%及以上; 与此相比, 盐度数据有效率偏低, 01、02和05号浮标有效率在90.00%左右, 03和04号浮标有效率在75.00%左右。五套浮标相比, 01号浮标温盐的数据有效率均为最高值, 且超过90.00%, 适宜以01号浮标数据为基准, 与其他浮标数据进行对比与分析。
3 温盐缺失数据处理 3.1 温盐缺失数据的统计与分析为了掌握数据缺失情况、选取合理的处理方法, 将五套浮标10 a的温盐数据, 分别按月进行了统计与汇总, 如表 5所示。将由设备损坏和维修等原因造成的缺失称为原始缺失, 其缺失率为24.50%。剔除异常数据后, 温盐数据缺失率分别为32.17%和32.33%。以02号浮标数据为例, 其10 a 12个月温盐数据最大值、最小值和平均值的统计结果, 如图 4a和4b所示, 图中线段的间断处为数据缺失区域。对于具有年际变化规律的温盐数据, 若忽略缺失数据(不处理缺失数据)进行数据分析与挖掘, 会影响温盐数据周期和季节等变化规律分析的准确性, 也可能会导致与真实分布或趋势产生偏差。数据缺失不仅会使曲线不连续或不完整, 也会使汇总的数据产生偏差; 如当仅有夏季数据时(02号浮标的2016年水温数据), 产生了年度平均值较高的情况, 如图 4c所示。若将缺失数据所在年度或月份进行删除, 如将02号浮标2016年整年的温盐数据删除, 会进一步加大数据的缺失量。因此, 为了更好地掌握研究海域年月时间序列的特性, 有必要对温盐的各月缺失数据进行插补处理。
| 特征 | 浮标号 | 缺失数据的月数/个 | 缺失比例 | 平均值 | ||||||||
| 原始数据 | 剔除异常 | 原始数据 | 剔除异常 | 原始数据 | 剔除异常 | |||||||
| 水温 | 01 | 8 | 24 | 6.67% | 20.00% | 24.50% | 32.17% | |||||
| 02 | 33 | 46 | 27.50% | 38.33% | ||||||||
| 03 | 30 | 35 | 25.00% | 29.17% | ||||||||
| 04 | 42 | 50 | 35.00% | 41.67% | ||||||||
| 05 | 34 | 38 | 28.33% | 31.67% | ||||||||
| 盐度 | 01 | 8 | 16 | 6.67% | 13.33% | 24.50% | 32.33% | |||||
| 02 | 33 | 44 | 27.50% | 36.67% | ||||||||
| 03 | 30 | 38 | 25.00% | 31.67% | ||||||||
| 04 | 42 | 59 | 35.00% | 49.17% | ||||||||
| 05 | 34 | 37 | 28.33% | 30.83% | ||||||||
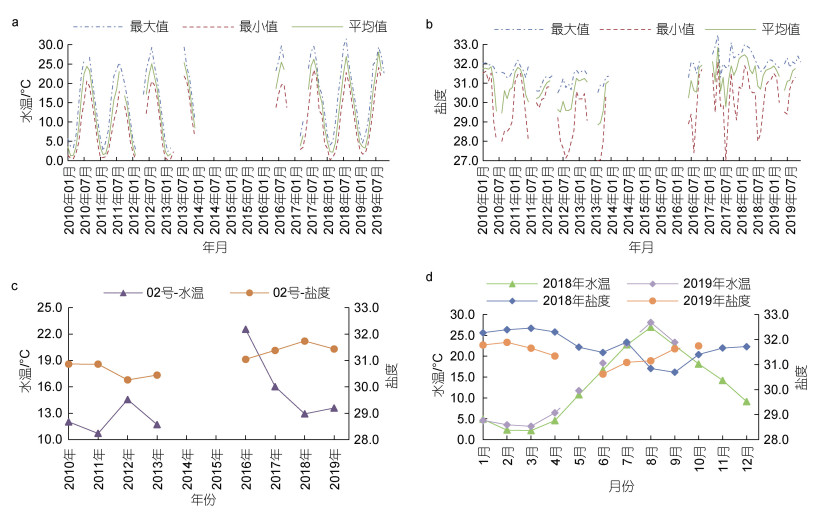 |
| 图 4 02号浮标月平均温盐 Fig. 4 Monthly mean temperature and salinity of buoy 02 注: a: 年水温有效率; b: 月水温有效率; c: 年盐度有效率; d: 月盐度有效率 |
同时, 由图 4可见, 相同月份温盐数据的梯度变化较小; 相邻年月数据间具有一定的相关性。以02号浮标2018和2019年月平均温盐数据为例, 2年的月平均水温的季节变化特征相同, 2019年各月水温略高, 如图 4c所示; 同理, 与2018年的月平均盐度相比, 2019年7月之前的盐度略低于2018年, 2019年8月之后的盐度略高于2018年, 如图 4d所示。若将汇总后的温盐数据视为矩阵, 即可采用矩阵等运算方法基于相邻关系等特性进行数据插补, 相当于基于相邻月份或不同年度相同月份等对各月缺失的温盐数据进行插补。
3.2 温盐缺失数据的处理和验证 3.2.1 缺失数据插补与分析针对研究数据中存在的原始缺失和剔除异常后的缺失问题, 选用Linear、Cubic、Lagrange、KNN、NNM、SoftImpute (SI)和IterativeImpute (Ⅱ)等方法分别对缺失的温盐数据进行插补; 综合考虑各浮标温盐数据的缺失范围(13.33%~49.17%), 如表 5所示, 将训练集的占比设计为50%、67%、75%、80%和90%等五种情况进行K-折交叉验证实验; 并采用均方误差MSE和决定系数R2对数据的插补效果与方法的拟合度进行分析; 在各种情况下, 重复实验10次取平均值作为实验结果, 如图 5所示。图 5中, 横坐标表示训练集所占比例, 纵坐标表示MSE或R2值。由于Linear和Cubic中的MSE较大, 未展示出其实验指标值。
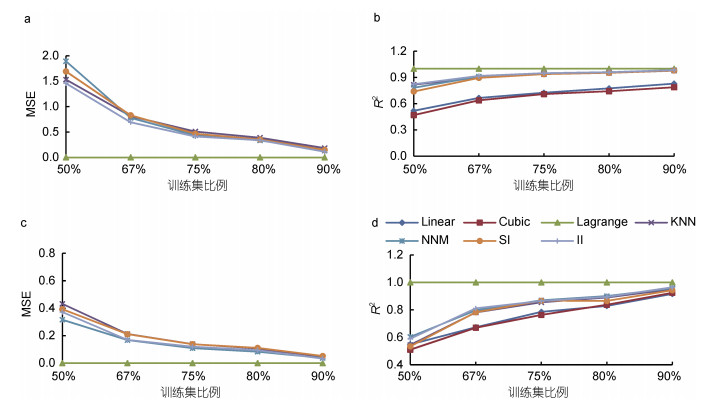 |
| 图 5 温盐数据插补效果 Fig. 5 Interpolation effect of temperature and salinity data 注: MSE: mean squared error, 均方误差; R2: 决定系数; a: 水温MSE; b: 水温R2; c: 盐度MSE; d: 盐度R2; Linear: 线性插补; Cubic: 三次样条插补; Lagrange: 拉格朗日插补; KNN: 最近邻插补; NNM: Nuclear- Norm Minimization, 核范数最小化插补; SI: SoftImpute, 软阈值插补; Ⅱ: IterativeImpute, 循环模型迭代插补 |
由图 5可见, 随着已知数据量的增加, 各种方法的数据插补效果均显著提升。当训练集占比为50%时, 温盐数据的MSE均为最大值, R2均为最小值。当训练集占比为90%时, 温盐数据的MSE均为最小值, R2均为最大值。各种方法的数据插补效果相比, Lagrange最佳, IterativeImpute次之。由于本文在数据统计时, 同时汇总了各月份数据的最大、最小和平均值; 对于平衡最大、最小和平均值关系上, Lagrange的效果较差; 此时, SoftImpute的效果最佳, 如图 6所示。但当存在整行(年)整列(月份)数据缺失值时, SoftImpute方法仅能填充0.00值; IterativeImpute方法可以有效解决这一问题, 即当整行(年)或整列(某个月10 a的数据)数据缺失时, 其插补效果显著优于其他方法。综上, 本文采用SoftImpute与IterativeImpute相结合的方法对温盐缺失数据进行插补填充。即先采用SoftImpute方法对温盐数据进行插补; 当存在值为0.00时, 再采用IterativeImpute方法进一步插补, 从而得到“完整”的数据集。在研究数据中, 已知数据平均占比与图 5中67%最接近; 此时, 温盐模型的R2值大约为0.9和0.8, 可见模型具有较高的拟合度。
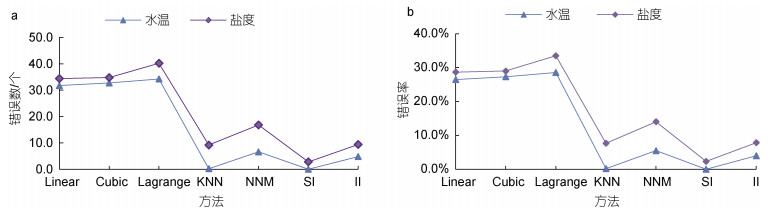 |
| 图 6 温盐数据插补错误情况 Fig. 6 Temperature and salinity data interpolation errors 注: Linear: 线性插补; Cubic: 三次样条插补; Lagrange: 拉格朗日插补; KNN: 最近邻插补; NNM: Nuclear- Norm Minimization, 核范数最小化插补; SI: SoftImpute, 软阈值插补; Ⅱ: IterativeImpute, 循环模型迭代插补; a: 平均错误数; b: 平均错误率 |
本节分别以02号浮标和整个研究海域为例, 对插补前后的温盐数据进行对比分析。
对于02号浮标的温盐数据, 分别从长期月平均时序序列、年平均和月平均三方面进行分析。与插补前数据相比, 插补后的数据具有优点如下: (1)得到了连续(不间断)的变化曲线, 体现了温盐以年度为单位的周期性变化特征, 如图 7a和7b所示; (2)修正了曲线中的异常点, 修正了图 7c中2016年水温的年平均值; (3)更好地展示了温盐的年际(线性)变化趋势, 如10 a水温数据呈现逐年显著线性升高趋势, 如图 7c所示; 10 a盐度数据呈现准平衡状态, 如图 7d所示; (4)完整体现了温盐的季节变化特征, 如图 7e和7f所示, 温盐四季变化近似于正余弦曲线, 基本呈现一峰一谷形式。与对比数据(4个坐标点的平均数据)相比, 水温插补后的数据与对比数据比较接近, 盐度插补后的数据与对比数据具有较类似的变化幅度。由此可见, 处理后的数据有助于提高对研究海域规律和特征挖掘与分析的准确性。
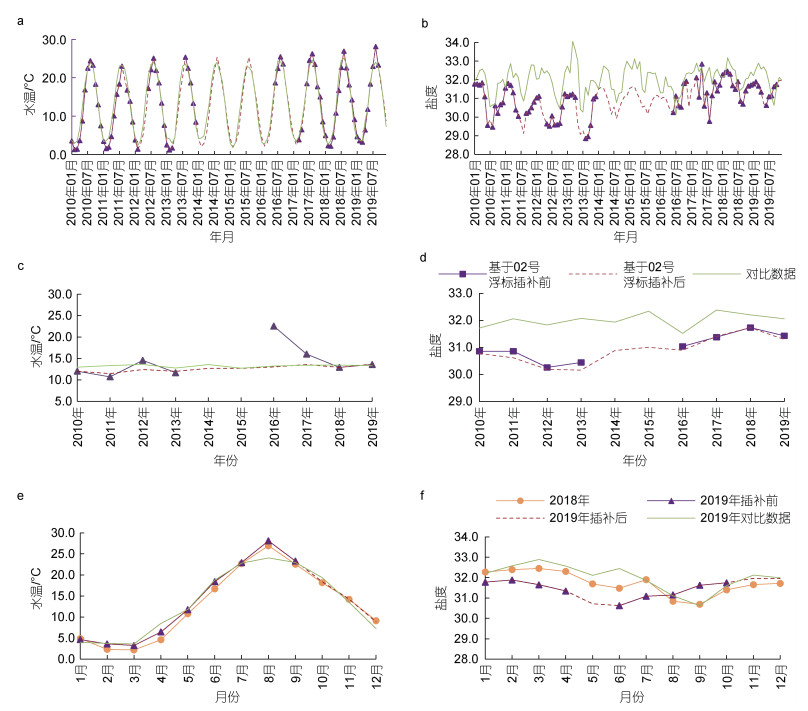 |
| 图 7 02号浮标温盐数据插补比较 Fig. 7 Comparison in temperature and salinity of buoy 02 注: a: 水温时间序列; b: 盐度时间序列; c: 年平均水温, d: 年平均盐度, e: 月平均水温, f: 月平均盐度 |
为了进一步验证插补后温盐数据的合理性和有效性, 先基于黄海站五套浮标插补前(剔除异常)和插补后的月平均序列数据求平均值, 得到该研究海域的温盐时序序列, 再与对比数据(4个坐标点的月平均序列的平均值)进行比较, 如图 8所示; 并从最小值、最大值、平均值和标准差等四方面进行统计分析, 如表 6所示。由图 8和表 6可见, 该海域总体温盐平均值分别为12.54 ℃和30.90, 标准差分别为7.88和0.71; 基于对比数据的总体温盐平均值分别为13.25 ℃和32.02, 标准差分别为7.76和0.72。与对比数据相比, 浮标的温盐数据值偏低; 总体上, 2个数据集中的温盐年际变化规律趋于一致; 插补后的标准差也与对比数据更接近。综上可见, 本研究处理后的数据合理可行, 可作为分析与研究该海域特征的基础数据。
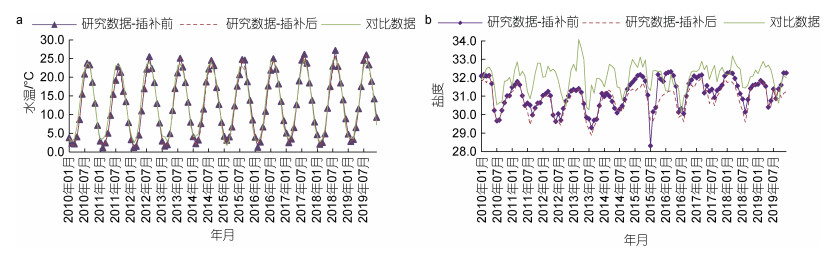 |
| 图 8 水温(a)和盐度(b)数据对比 Fig. 8 Comparison in temperature and salinity data |
| 特征 | 浮标 | 最小值 | 最大值 | 平均值 | 标准差 |
| 水温/℃ | 研究数据-插补前 | 1.11 | 27.19 | 12.72 | 8.01 |
| 研究数据-插补后 | 1.43 | 26.02 | 12.54 | 7.88 | |
| 对比数据 | 1.75 | 25.05 | 13.25 | 7.76 | |
| 盐度 | 研究数据-插补前 | 28.31 | 32.91 | 31.13 | 0.81 |
| 研究数据-插补后 | 28.87 | 32.11 | 30.90 | 0.71 | |
| 对比数据 | 30.11 | 34.07 | 32.02 | 0.72 |
基于2010~2019年北黄海长海县附近海域的海洋表层温盐数据, 首先采用简单统计量分析了原始数据的基本结构和特征; 其次基于2σ原则和箱型图法确定了数据界限, 标定并处理了异常数据; 再次, 对10 a每个月份的文件数据进行了统计与汇总, 并将原始缺失和异常数据均作为缺失数据处理; 最后, 采用SoftImpute与IterativeImpute相结合的方法实现了温盐各月缺失数据的插补, 从而提高了温盐数据的质量。本研究的相关结论如下。
(1) 辨识异常数据的本质问题是, 通过分析原始数据的基本特性合理确定数据界限。其中, 水温数据适合采用2σ原则确定上下界限为[0.00 ℃, 31.00 ℃], 盐度数据适合采用箱型图法确定上下界限为[27.00, 34.00]。不在该界限范围内的数据标定为异常数据。剔除异常数据后, 水温数据有效率十分理想, 平均达到99.76%; 盐度数据有效率平均达到84.15%。
(2) 对于具有年际变化规律的温盐数据, 适合基于统计学原理采用矩阵等运算方法实现数据插补; 本文采用SoftImpute与IterativeImpute相结合的方法插补了浮标中的缺失数据, 该方法具有较低的均方误差和较高的模型拟合度。数据插补后, 温盐数据曲线连续、平滑、变化与趋势更加显著, 且可以修正曲线中的异常点。与对比数据温盐年际变化趋势基本一致, 其标准差也比较接近。
(3) 五套浮标相比, 01号浮标温盐的数据有效率均为最高值; 01号浮标温盐的数据缺失率均为最低值。可见01号浮标的数据质量最高且较完整, 适宜以01号浮标数据为基准, 与其他数据进行对比与分析; 或对其他浮标中数据进行校正和插补。
本文主要采用经典的数据分析与处理方法, 对浮标温盐缺失数据进行插补。在后续研究中, 可综合考虑温盐数据的相关性进行缺失数据插补, 可基于多年的时序数据采用神经网络预测模型实现温盐缺失数据的插补, 还可从不同的时空维度进行数据插补, 进一步提升数据的精准性和有效性。在此基础上, 对海洋温盐数据进行分析与挖掘研究, 从而对海洋的温盐特征、变化规律和发展趋势等有更进一步的了解, 并为海洋防灾减灾、科学研究等提供更有价值的参考。
致谢 本文数据来源于中国科学院海洋研究所黄海站的五套浮标。感谢中国科学院近海海洋观测研究网络黄海站所有工作人员的大力支持和付出。
石强. 2013. 北黄海冬季温盐年际变化时空模态与气候响应. 海洋通报, 32(6): 633-640 |
石强. 2014. 南黄海冬季温盐年际变化时空模态与气候响应. 海洋通报, 33(2): 148-156, 162 |
石强. 2016. 北黄海夏季温盐年际变化时空模态与气候响应. 应用海洋学学报, 35(4): 469-483 DOI:10.3969/J.ISSN.2095-4972.2016.04.003 |
石强. 2019. 南黄海夏季温盐年际变化时空模态与气候响应. 应用海洋学学报, 38(2): 169-181 DOI:10.3969/J.ISSN.2095-4972.2019.02.003 |
卢勇夺, 王朝阳, 王豹, 等. 2019. 我国海洋锚系浮标数据异常值检测方法研究——以QF110和QF306为例. 海洋预报, 36(6): 37-43 |
刘宇, 2020. 基于海洋时序数据的温度预测与补全方法研究[D]. 长春: 吉林大学硕士学位论文.
|
刘长华, 王彦俊. 2017. 中国科学院近海海洋观测研究网络黄海站、东海站观测数据集: 2009.06-2010.12. 北京: 海洋出版社
|
刘长华, 冯立强. 2018. 中国科学院近海海洋观测研究网络黄海站、东海站观测数据图集-Ⅱ. 北京: 海洋出版社
|
刘长华, 王春晓, 王旭, 等. 2019a. 锚定式海洋水体剖面观测技术的研究与应用. 海洋科学, 43(12): 139-147 |
刘长华, 李一凡. 2019b. 中国科学院近海海洋观测研究网络黄海站、东海站观测数据图集-Ⅷ. 北京: 海洋出版社
|
刘长华, 张曙伟, 王旭, 等. 2020. 三锚式浮标综合观测平台的研究和应用. 海洋科学, 44(1): 148-156 |
齐庆华, 蔡榕硕. 2019. 中国近海海表温度变化的极端特性及其气候特征研究. 海洋学报, 41(7): 36-51 DOI:10.3969/j.issn.0253-4193.2019.07.004 |
刘首华, 陈满春, 董明媚, 等. 2016. 一种实用海洋浮标数据异常值质控方法. 海洋通报, 35(3): 264-270 |
孙晓丽, 郭艳, 李宁, 等. 2021. 基于改进神经过程的缺失数据填充算法. 中国科学院大学学报, 38(2): 280-287 |
张宇, 周燕, 陶邦一, 等. 2020. 基于时序相关性分析方法的浮标异常数据识别. 海洋学报, 42(11): 131-141 |
张博, 曾丽丽, 陈举, 等. 2018. 基于南海北部开放航次观测的2004—2005年次表层盐度异常特征与形成机制. 海洋与湖沼, 49(1): 9-16 |
张良均, 王路, 谭立云, 等. 2018. Python数据分析与挖掘实战. 北京: 机械工业出版社, 34-35, 60-64
|
陈海洋, 刘喜庆, 环晓敏. 2020. 一步预测的SVDDBN缺失数据插补算法. 计算机工程与应用, 56(7): 81-87 |
张翠翠, 魏皓, 宋贵生, 等. 2020. 基于IPCC-CMIP5的中国东部近海表层水温未来预估分析. 海洋与湖沼, 51(6): 1288-1300 |
赵聪蛟, 孔梅, 孙笑笑, 等. 2016. 浙江省海洋水质浮标在线监测系统构建及应用. 海洋环境科学, 35(2): 288-294 |
钱程程, 陈戈. 2018. 海洋大数据科学发展现状与展望. 中国科学院院刊, 33(8): 884-891 |
黄冬梅, 邹国良. 2016. 海洋大数据. 上海: 上海科学技术出版社
|
鲍献文, 李娜, 姚志刚, 等. 2009. 北黄海温盐分布季节变化特征分析. 中国海洋大学学报, 39(4): 553-562 |
BENMARHNIA T, DEGUEN S, KAUFMAN J S et al, 2015. Review article: vulnerability to heat-related mortality: a systematic review, meta-analysis, and meta-regression analysis. Epidemiology, 26(6): 781-793 DOI:10.1097/EDE.0000000000000375 |
CHAN K, LEE T W, SEJNOWSKI T J, 2003. Variational Bayesian learning of ICA with missing data. Neural Computation, 15(8): 1991-2011 DOI:10.1162/08997660360675116 |
CHEN L S, PRENTICE R L, WANG P, 2014. A penalized EM algorithm incorporating missing data mechanism for Gaussian parameter estimation. Biometrics, 70(2): 312-322 DOI:10.1111/biom.12149 |
CHENG L J, ABRAHAM J, TRENBERTH K E et al, 2021. Upper ocean temperatures hit record high in 2020. Advances in Atmospheric Sciences, 38(4): 523-530 DOI:10.1007/s00376-021-0447-x |
CHENG L J, TRENBERTH K E, FASULLO J et al, 2017. Improved estimates of ocean heat content from 1960 to 2015. Science Advances, 3(3): e1601545 DOI:10.1126/sciadv.1601545 |
FARIA R, GOMES M, EPSTEIN D et al, 2014. A guide to handling missing data in cost-effectiveness analysis conducted within randomised controlled trials. Pharmacoeconomics, 32(12): 1157-1170 DOI:10.1007/s40273-014-0193-3 |
LGUENSAT R, TANDEO P, AILLIOT P, et al, 2016. Using archived datasets for missing data interpolation in ocean remote sensing observation series[C]//OCEANS 2016-Shanghai. Shanghai: IEEE: 1-5.
|
LIU Y J, QIU M, LIU C, et al, 2016. Big data in ocean observation: opportunities and challenges[C]//Second International Conference on Big Data Computing and Communications. Shenyang: Springer: 212-222.
|
QIN M J, DU Z H, ZHANG F et al, 2019. A matrix completion-based Multiview learning method for imputing missing values in buoy monitoring data. Information Sciences, 487: 18-30 DOI:10.1016/j.ins.2019.02.057 |
SKRONDAL A, RABE-HESKETH S, 2014. Protective estimation of mixed-effects logistic regression when data are not missing at random. Biometrika, 101(1): 175-188 DOI:10.1093/biomet/ast054 |
ZHANG K K, GONZALEZ R, HUANG B et al, 2015. Expectation-maximization approach to fault diagnosis with missing data. IEEE Transactions on Industrial Electronics, 62(2): 1231-1240 DOI:10.1109/TIE.2014.2336635 |
 2022, Vol. 53
2022, Vol. 53


